Matlab偏微分方程有限差分法深入解析

数值求解变系数对流方程初边值问题

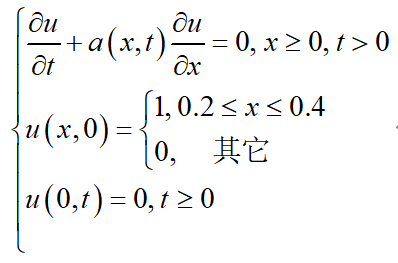
%%偏微分方程有限差分法实习题
%%算例四
%==================================================
%输入
clear all
dx=[0.01 0.02];                   %Δh
dt=0.01;                             %题目中未给出Δt,易知max(a)为1,根据稳定条件需Δt≤Δh.
X=[0 1.5];                           %x的取值范围,格式必须从最小到最大
T=[0.1,0.5,1.0];                   %截止时间T
UL0=0;                               %边界条件
%==================================================
%解析解
xx=0:0.01:1;                        % 单独计算解析解区间
for k=1:size(T,2)
%解析解公式:
u=0.*((xx-T(k)./(1+xx.*xx))<0.2)+1.*((xx-T(k)./(1+xx.*xx))>=0.2&(xx-T(k)./(1+xx.*xx))<=0.4)+0.*((xx-T(k)./(1+xx.*xx))>0.4);
%绘图
subplot(size(dx,2),size(T,2),k);
plot(xx,u);                            %默认实线为解析解真值
hold on
subplot(size(dx,2),size(T,2),k+3);
plot(xx,u);
hold on
end
%==================================================
%差分格式解
for i=1:size(dx,2)
    for j=1:size(T,2)
    x=0:dx(i):X(2);                  %列出每个x
    t=0:dt:T(j);                        %列出每个t
    uu=UL0.*ones(size(t,2),size(x,2)) ;   %【迎风格式】边界,顺便提前分配内存
    LF=UL0.*ones(size(t,2),size(x,2)) ;   %【Lax-Friedrichs格式】边界
    LW=UL0.*ones(size(t,2),size(x,2)) ;   %【Lax-Wendroff格式】边界
    uu(1,:)=0.*(x<0.2)+1.*(x>=0.2&x<=0.4)+0.*(x>0.4); %【迎风格式】初始条件
    LF(1,:)=0.*(x<0.2)+1.*(x>=0.2&x<=0.4)+0.*(x>0.4); %【Lax-Friedrichs格式】初始条件
    LW(1,:)=0.*(x<0.2)+1.*(x>=0.2&x<=0.4)+0.*(x>0.4); %【Lax-Wendroff格式】初始条件
        for m=2:size(t,2)           %时间上有11层
            for n=2:size(x,2)       %空间上有151或者76列
            %每个节点对应的a,易知必然0<a≤1
            a(m,n)=(1+x(n)^2)/(1+2*x(n)*t(m)+2*x(n)^2+x(n)^4);
            %迎风格式
            uu(m,n)=uu(m-1,n)-a(m,n)*dt/dx(i)*(uu(m-1,n)-uu(m-1,n-1));
            end
            for n=2:size(x,2)-1
            %Lax-Friedrichs格式
            LF(m,n)=0.5*((1+a(m,n)*dt/dx(i))*LF(m-1,n-1)+(1-a(m,n)*dt/dx(i))*LF(m-1,n+1));
            %Lax-Wendroff格式
            LW(m,n)= LW(m-1,n)-0.5*a(m,n)*dt/dx(i)*(LW(m-1,n+1)-LW(m-1,n-1))+0.5*a(m,n)*a(m,n)*dt/dx(i)*dt/dx(i)*(LW(m-1,n+1)-2*LW(m-1,n)+LW(m-1,n-1));
            end
        end
%==================================================
        %绘图
        hold on
        subplot(size(dx,2),size(T,2),3*i+j-3);
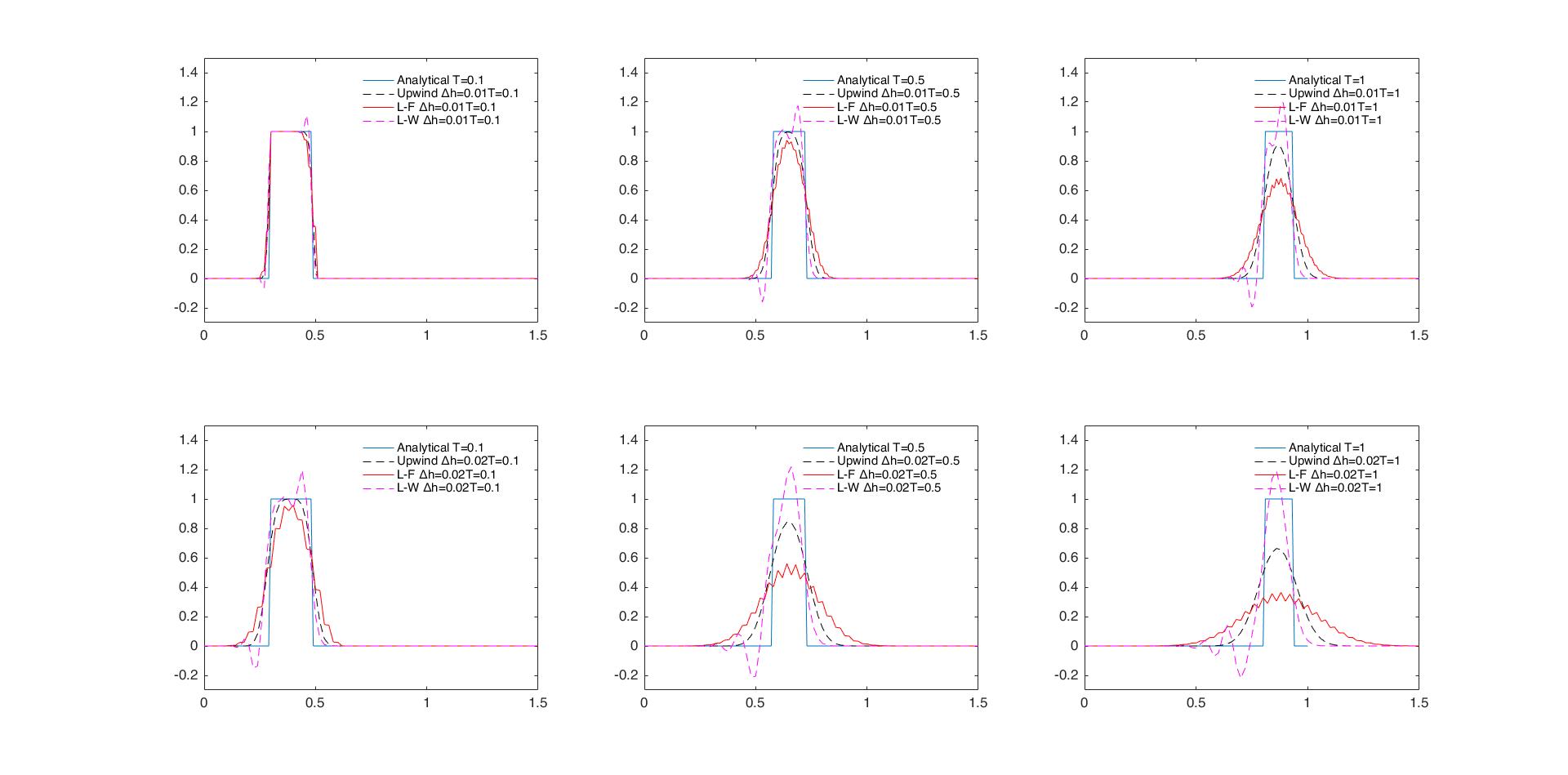
        plot(x,uu(size(t,2),:),'k--');  %黑色虚线表示迎风格式
        plot(x,LF(size(t,2),:),'r');   %红色实线表示Lax-Friedrichs格式
        plot(x,LW(size(t,2),:),'g--'); %绿色虚线表示Lax-Wendroff格式
        str{j}=['Analytical T=' num2str(T(j))];
        str1{i,j}=['Upwind Δh=' num2str(dx(i)) 'T=' num2str(T(j))];
        str2{i,j}=['L-F Δh=' num2str(dx(i)) 'T=' num2str(T(j))];
        str3{i,j}=['L-W Δh=' num2str(dx(i)) 'T=' num2str(T(j))];
        legend(str{j},str1{i,j},str2{i,j},str3{i,j}); %生成图例
        legend('boxoff') %消除图例边框和背景
        xlim([0 1.5]);    %画个合适的坐标轴
        ylim([-0.3 1.5]);
        end
end
%==================================================

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删