软件
产品
求解无粘Burgers方程的初值问题:
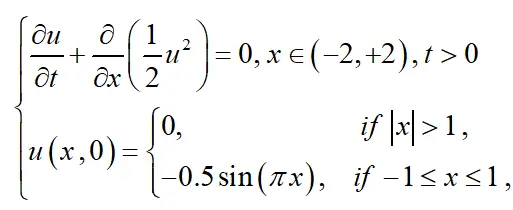

==========答案===========
%%偏微分方程有限差分法实习题
%%算例六
%==================================================
%输入
clc;clear all
dx=0.02;%Δh
dt=0.02;%Δt
X=[-2 2];%x的取值范围,格式必须从最小到最大
T=[0.32 0.96];%截止时间T
UL0=0; %边界条件
%==================================================
%初始值
x=X(1):dx:X(2);
for k=1:size(T,2)
%解析解公式:
u=0.*(x<-1)+(-0.5*sin(pi*x)).*(x>=(-1)&x<=1)+0.*(x>1);
%绘图
subplot(1,2,k);
plot(x,u); %默认实线为解析解真值
hold on
end
%==================================================
%差分格式解
for i=1:size(T,2)
t=0:dt:T(i);
LF=UL0.*ones(size(t,2),size(x,2)) ; %【Lax-Friedrichs格式】边界
uu=UL0.*ones(size(t,2),size(x,2)) ; %【迎风格式】边界
LW=UL0.*ones(size(t,2),size(x,2)) ; %【Lax-Wendroff格式】边界
LF(1,:)=0.*(x<-1)+(-0.5*sin(pi*x)).*(x>=(-1)&x<=1)+0.*(x>1);%【Lax-Friedrichs格式】初始条件
uu(1,:)=0.*(x<-1)+(-0.5*sin(pi*x)).*(x>=(-1)&x<=1)+0.*(x>1);%【迎风格式】初始条件
LW(1,:)=0.*(x<-1)+(-0.5*sin(pi*x)).*(x>=(-1)&x<=1)+0.*(x>1);%【Lax-Wendroff格式】初始条件
for m=2:size(t,2) %时间上有16层
for n=2:size(x,2)-1 %空间上
%Lax-Friedrichs格式
LF(m,n)=0.5*(LF(m-1,n+1)+LF(m-1,n-1))-0.25*dt/dx*(LF(m-1,n+1)*LF(m-1,n+1)-LF(m-1,n-1)*LF(m-1,n-1));
%Lax-Wendroff格式
LW(m,n)=LW(m-1,n)-0.25*dt/dx*(LW(m-1,n+1)*LW(m-1,n+1)-LW(m-1,n-1)*LW(m-1,n-1))+0.125*dt/dx*dt/dx*((LW(m-1,n)+LW(m-1,n+1))*(LW(m-1,n+1)*LW(m-1,n+1)-LW(m-1,n-1)*LW(m-1,n-1))-(LW(m-1,n)+LW(m-1,n-1))*(LW(m-1,n)*LW(m-1,n)-LW(m-1,n-1)*LW(m-1,n-1)));
end
for n=2:size(x,2)
%迎风格式
uu(m,n)=uu(m-1,n)-0.5*dt/dx*(uu(m-1,n)*uu(m-1,n)-uu(m-1,n-1)*uu(m-1,n-1));
end
end
%==================================================
%绘图
hold on
subplot(1,2,i);
plot(x,LF(size(t,2),:),'r-'); %红色实线表示 Lax-Friedrichs格式
plot(x,uu(size(t,2),:),'k--'); %黑色虚线表示 迎风格式
plot(x,LW(size(t,2),:),'g-'); %绿色实线表示Lax-Wendroff格式
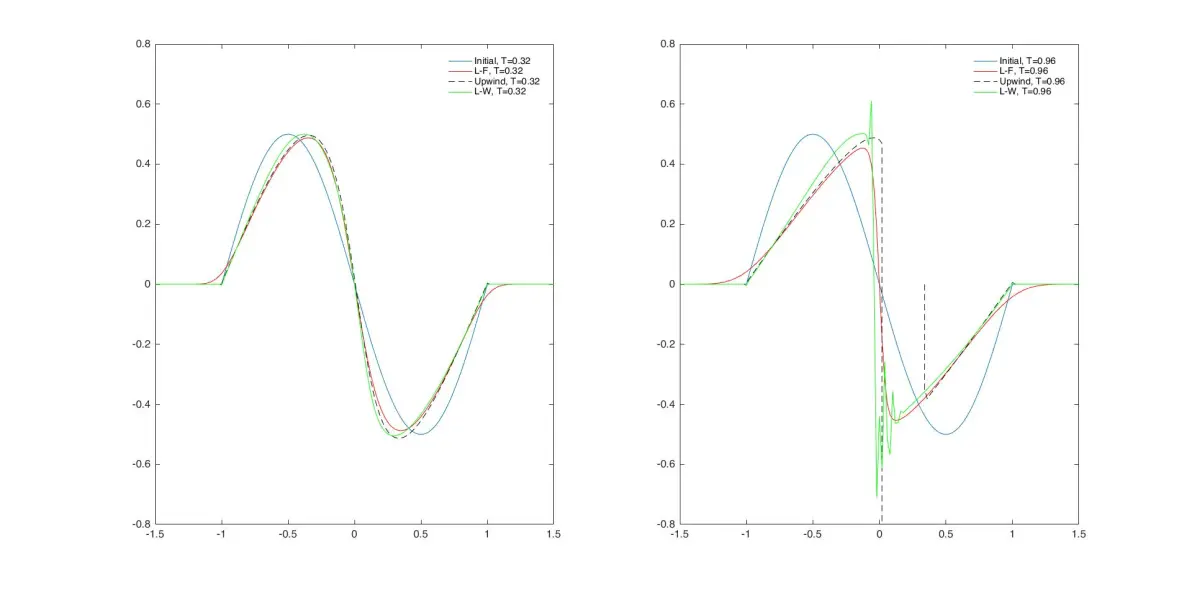
str{i}=['Initial, T=' num2str(T(i))];
str1{i}=['L-F, T=' num2str(T(i))];
str2{i}=['Upwind, T=' num2str(T(i))];
str3{i}=['L-W, T=' num2str(T(i))];
legend(str{i},str1{i},str2{i},str3{i}); %生成图例
legend('boxoff') %消除图例边框和背景
xlim([-1.5 1.5]);
ylim([-0.8 0.8]);
end
%==================================================