产品
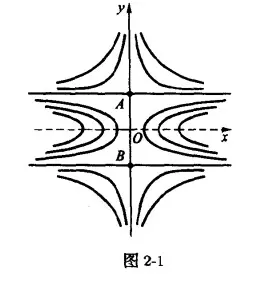
最近在复习常微分方程,看丁同仁教材27页时看到上面粗制滥造的手画线素场都什么年代还在画传统线素场,遂萌生了自己画一个的想法,正好也很久没用matlab了,花了点时间写出来。
方程是
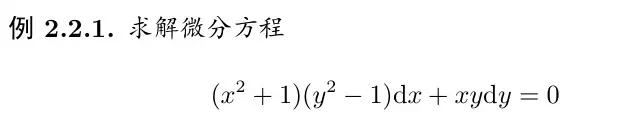
分离变量解出来的通解是
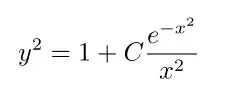
用matlab画出线素场,并画上三条特解的曲线(一眼顶真)
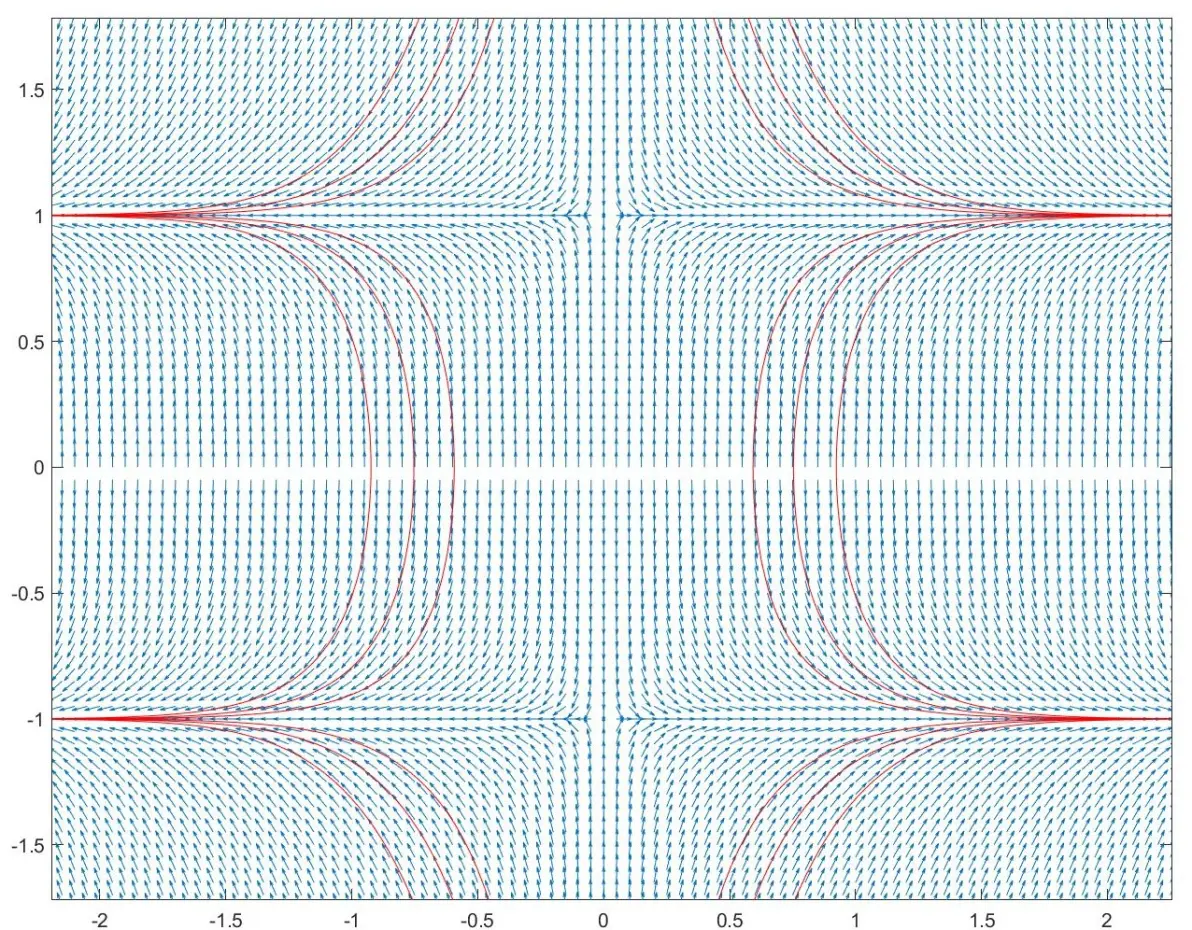
对比丁同仁上的传统线素场
最后附上matlab代码(很久不用matlab了,有点土法炼钢的味道,若有更好的绘制方法,欢迎分享)
clear all;
close all;
clc;
y = -5:0.05:5;%%xy的一维数据
x = -5:0.05:5;
f = @(x,y) -(x^2+1)*(y^2-1)*x^(-1)*y^(-1);
[x,y] = meshgrid(x,y);%%生成[x,y]格点
%下面处理格点位置的向量,要使左半平面的向量相反
for i=1:1:201
for j=1:1:201
if x(i,j)<0
vx(i,j)=-cos(atan(f(x(i,j),y(i,j))));
vy(i,j)=-sin(atan(f(x(i,j),y(i,j))));
else
vx(i,j)=cos(atan(f(x(i,j),y(i,j))));
vy(i,j)=sin(atan(f(x(i,j),y(i,j))));
end
end
end
quiver(x,y,vx,vy);%%生成向量图
hold on
%下面绘制方程某些特解的曲线
g1=@(x,y) y.^2-1+exp(-x.^2)./x.^2
fimplicit(g1,'r',[-5,5]);
hold on
g2=@(x,y) y.^2-1+0.5*exp(-x.^2)./x.^2
fimplicit(g2,'r',[-5,5]);
hold on
g3=@(x,y) y.^2-1+2*exp(-x.^2)./x.^2
fimplicit(g3,'r',[-5,5]);
hold on
g4=@(x,y) y.^2-1-1*exp(-x.^2)./x.^2
fimplicit(g4,'r',[-5,5]);
hold on
g5=@(x,y) y.^2-1-0.5*exp(-x.^2)./x.^2
fimplicit(g5,'r',[-5,5]);
hold on
g6=@(x,y) y.^2-1-2*exp(-x.^2)./x.^2
fimplicit(g6,'r',[-5,5]);
hold on
axis equal;