MATLAB命令ode45：轻松求解常微分方程

常微分方程在物体运动, 热量传导，生态系统震荡，混沌现象，厄尔尼诺等等方面都有重要的应用。使用matlab命令ode45可以轻松求解这些常微分方程。

例1：(生态系统的振荡现象)

第一次世界大战中，因为战争很少捕鱼，按理战后应能捕到更多的鱼才是。可是大战后，在地中海却捕不到鲨鱼，因而渔民大惑不解。

      令x1为鱼饵的数量，x2为鲨鱼的数量，t为时间。微分方程为

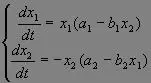
式中a1, a2, b1, b2都是正常数。第一式鱼饵x1的增长速度大体上与x1成正比，即按a1x1比率增加, 而被鲨鱼吃掉的部分按b1x1x2的比率减少；第二式中鲨鱼的增长速度由于生存竞争的自然死亡或互相咬食按a2x2的比率减少，但又根据鱼饵的量的变化按b2x1x2的比率增加。对a1=3, b1=2, a2=2.5, b2=1, x1(0)=x2(0)=1求解。

画出解曲线图如下，可以观察到鱼饵和鲨鱼数量的周期振荡现象。

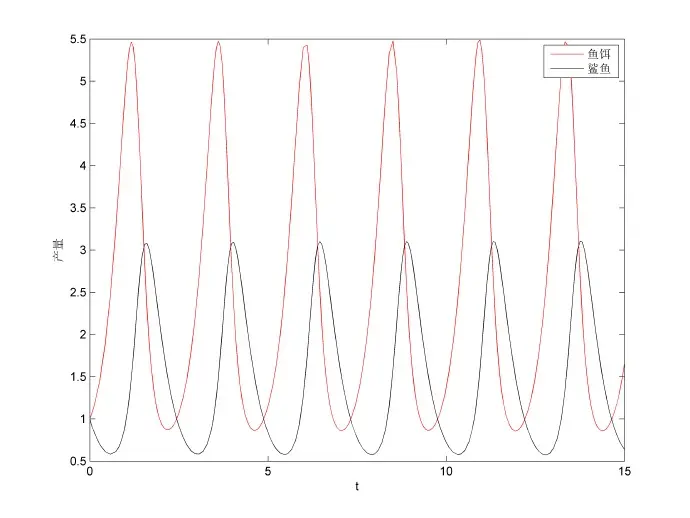
程序如下：

先编写函数文件：

function f = eg2_4(t,x)

f(1)=3*x(1)-2*x(2)*x(1);

f(2)=-2.5*x(2)+x(2)*x(1);

f=f(:);

接着调用函数：

clear; [t,x]=ode45(@eg2_4,[0 15],[1;1]); plot(t,x(:,1),'r',t,x(:,2),'k'); xlabel('t') ylabel('产量') legend('鱼饵','鲨鱼')