Abaqus渐进损伤与失效（2.2）：延性金属损伤起始准则

终于学到每种损伤起始准则的具体描述了，fighting！

cut-off

延性金属的材料损伤起始准则：

通常用于预测金属损伤起始，包括金属以及其他材料的成板、挤压、铸造；

可以与延性金属损伤演化模型结合使用；

允许指定一个及以上的损伤起始准则；

包括延性ductile、剪切shear、成形极限图(forming limit diagram, FLD)、成形极限应力图( forming limit stress diagram,FLSD)和Müschenborn-Sonne成形极限图(MSFLD)损伤起始准则；

在Abaqus/Explicit中包含Marciniak-Kuczynski (M-K) and Johnson-Cook损伤起始准则；

在Abaqus/Explicit中Mises和Johnson-Cook塑性(韧性、剪切、FLD、FLSD、MSFLD、Johnson-Cook和MK标准)可联合使用；Hill和Drucker-Prager塑性(韧性、剪切、FLD、FLSD、MSFLD和Johnson-Cook标准)可结合使用。

cut-off

1. 金属断裂损伤起始准则

导致延性金属断裂的两种主要机制：由孔洞的形核、生长和聚并引起的延性断裂，以及剪切带局部化导致的剪切断裂。基于现象学观察，这两种机制需要不同形式的损伤起始标准。

1.1 延性准则 Ductile criterion

延性损伤准则是一种现象学模型，用于预测由于孔洞的成核、生长和合并而引起的损伤。

模型假设损伤开始时的等效塑性应变是应力三轴度和应变率的函数：

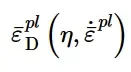
损伤开始时的等效塑性应变

式中η =−p / q为应力三轴度，p为压应力，q为Mises等效应力，˙¯ε pl为等效塑性应变率。

当满足以下条件时，开始损伤：

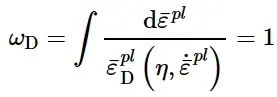
损伤标准

其中ω D是随塑性变形单调增加的状态变量。在分析期间的每个增量中，ω D的增量计算为：

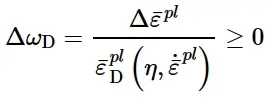
在Abaqus/Standard中，延性准则可以与Mises、Johnson-Cook、Hill和Drucker-Prager塑性模型结合使用；在Abaqus/Explicit中，可以与Mises、Johnson-Cook、Hill和Drucker-Prager塑性模型(包括状态方程)结合使用。

延性损伤准则定义的位置

★ 定义延性准则对矿脉角Lode angle的依赖关系

最近对铝合金和其他金属的实验结果(Bai和Wierzbicki, 2008)表明，除了应力三轴度和应变率外，延性断裂还取决于与Lode角(或偏极角)有关的偏应力第三不变量。

Abaqus/Explicit和Abaqus/Standard都允许定义塑性损伤开始时的等效塑性应变，¯ε pl D，作为Lode角Θ的函数，以函数形式表示：

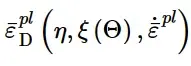
其中：

q是Mises等效应力，r是偏应力的第三不变量，

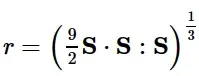
函数ξ (Θ)取值范围从压缩的应力状态ξ =−1到拉伸应力状态ξ = 1。

在Abaqus/CAE中不支持定义延性判据与Lode角的依赖关系，通过输入文件定义：

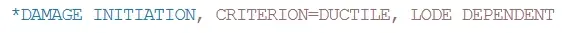
★ Johnson-Cook准则 Johnson-Cook criterion

Johnson-Cook准则(仅在Abaqus/Explicit中可用)是延性准则的一种特殊情况，其中假定损伤开始时的等效塑性应变为¯ε pl D的形式为：

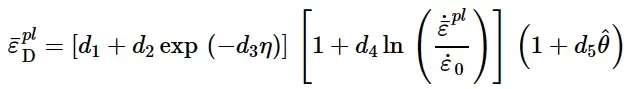
损伤起始时的等效塑性应变

其中d1 ~ d5为失效参数，˙ε 0为参考应变率。这个表达式与Johnson和Cook(1985)发表的原始公式的不同之处在于参数d3的符号。这种差异的原因是，大多数材料的¯ε pl D都会随着应力三轴度的增加而减小，因此，上式中的d3通常取正值。θ为无量纲温度，定义为：

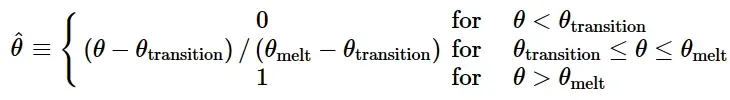
式中，θ为当前温度，θ melt为熔融温度，θ transition为转变温度，定义为与损伤应变¯ε p l D表达式无关的温度。

材料参数必须在或低于转变温度下测量。

Johnson-Cook准则可以与Mises、Johnson-Cook、Hill和Drucker-Prager塑性模型(包括状态方程)结合使用。当与Johnson-Cook塑性模型结合使用时，熔融温度和转变温度的值应与塑性定义中的值一致。Johnson-Cook损伤起始准则也可以与任何其他损伤起始准则一起指定，包括延性准则，每个起始准则被独立处理。

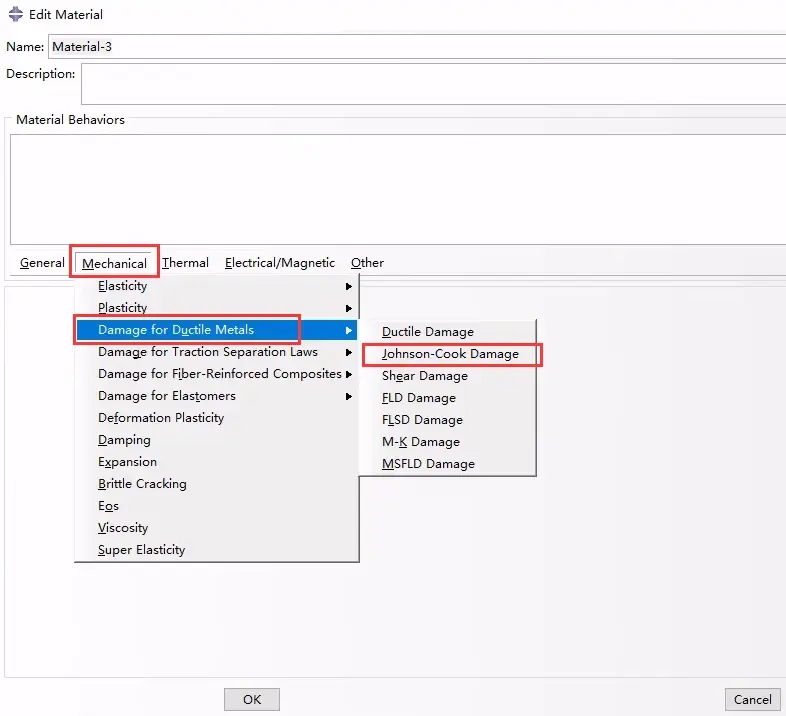
Johnson-Cook criterion的CAE定义位置

1.2 剪切准则 Shear criterion

剪切准则是预测剪切带局部化损伤发生的一种现象学模型。模型假设损伤开始时的等效塑性应变是剪切应力比和应变率的函数：

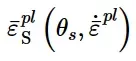
损伤开始时的等效塑性应变

其中：

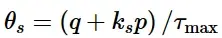
剪应力比；τ Max为最大剪应力，k s为材料参数，铝的k s的典型值是k s = 0.3。

当满足以下条件时，符合损伤起始标准：

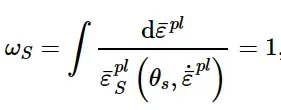
式中，ω S为状态变量，与等效塑性应变的增量变化成正比，随塑性变形单调增加。

在分析过程中的每个增量，ω S的增量计算为：

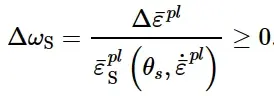
在Abaqus/Explicit中，剪切准则可以与Mises、Johnson-Cook、Hill和Drucker-Prager塑性模型(包括状态方程)结合使用。在Abaqus/Standard中，它可以与Mises、Johnson-Cook、Hill和Drucker-Prager模型一起使用。

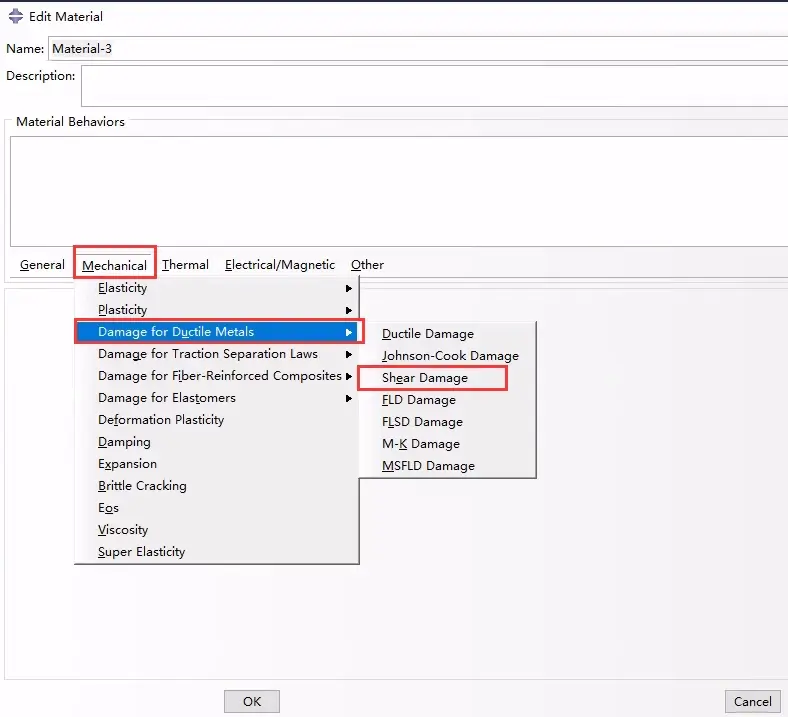
剪切损伤起始准则的CAE定义位置

1.3 非线性的损伤积累

用上述损伤累积的线性形式得到的数值结果与实验结果并不总是很吻合。结果表明，如果采用基于幂律规则的公式来表征损伤累积的非线性，可以得到更好的一致性。该幂律公式适用于Abaqus/Standard和Abaqus/Explicit中的延性和剪切准则，以及Abaqus/Explicit中的Johnson Cook准则。对于延性和Johnson Cook准则，其形式为：

对于剪切准则，可表示为：

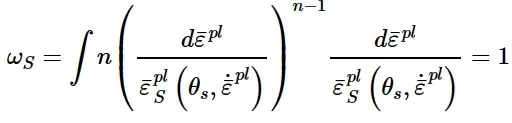
式中n为累积幂。

注意：在Abaqus/CAE中不支持定义累积幂的值，通过输入文件定义：

1.4 初始条件

可选地，可以通过提供初始等效塑性应变值来指定材料的初始工作硬化状态，如果残余应力也存在，则定义初始应力值。Abaqus使用这些信息初始化延性和剪切损伤起始准则ω D和ω S的值，并假设应力三轴度和剪应力比(线性应力路径)恒定。

2. 金属薄板失稳损伤起始准则

颈缩失稳是板料成形过程中的决定性因素：局部颈缩的大小通常是板料厚度的数量级，局部颈缩可以迅速导致断裂。由于颈缩的大小与单元的厚度成数量级，局部颈缩无法用传统的壳单元进行模拟。

Abaqus支持预测金属板颈缩不稳定性的四个准则： forming limit diagram (FLD); forming limit stress diagram (FLSD); Müschenborn-Sonne forming limit diagram (MSFLD); 以及在Abaqus/Explicit中可用的Marciniak-Kuczynski (M-K) 准则。这些准则仅适用于具有平面应力公式的单元(平面应力、壳、连续壳和膜单元)；对于其他的单元，abaqus忽略这些准则。颈缩失稳的起始准则可损伤演化模型相结合，用于模拟颈缩引起的损伤。

经典的基于应变的成形极限图(FLDs)依赖于应变路径。变形模式的改变(例如，等双轴加载后单轴拉伸应变)可能导致极限应变水平的重大变化。因此，当分析中的应变路径为非线性时，应谨慎使用FLD损伤起始准则。在实际的工业应用中，应变路径的显著变化可能是由多步成形操作、工具的复杂几何形状和界面摩擦等因素引起的。对于具有高度非线性应变路径的问题，Abaqus提供了三个另外的损伤起裂准则： the forming limit stress diagram (FLSD) criterion, the Müschenborn-Sonne forming limit diagram (MSFLD) criterion, and in Abaqus/Explicit the Marciniak-Kuczynski (M-K) criterion; 这些替代FLD损伤起始准则的方法旨在将加载路径依赖性最小化。

下面将讨论Abaqus中用于预测金属板损伤起始的每个准则的特点。

2.1 成形极限图准则 Forming limit diagram (FLD) criterion

（力学概念：主应变：是材料力学中描述应变的一个概念，指与主应力σ1、σ2、σ3相对应的线应变ε1、ε2、ε3。）

成形极限图(FLD)是Keeler和Backofen(1964)提出的一个有用的概念，用于确定材料在颈缩不稳定发生之前可以承受的变形量。在缩颈发生之前板材材料所能承受的最大应变称为成形极限应变。FLD是在主对数应变空间(面内)中的成形极限应变图。在接下来的讨论中，最大极限应变和最小极限应变分别是指平面内主极限应变的最大值和最小值。最大极限应变通常表示在纵轴上，最小极限应变表示在横轴上，如图1所示。连接变形变得不稳定状态的线称为成形极限曲线(FLC)。FLC给出了一种板材材料的可成形性的感觉。通过Abaqus计算的应变可以与FLC进行比较，以确定所分析的成形过程的可行性。

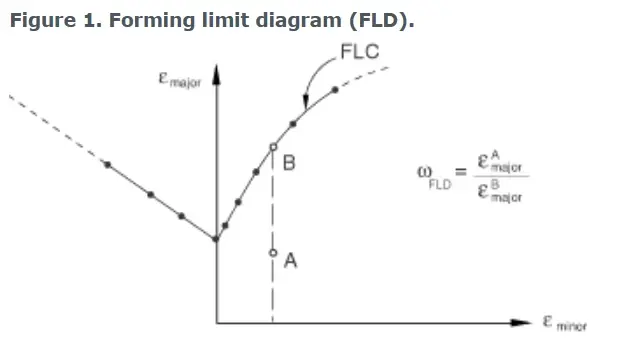
图1 FLD曲线

FLD损伤起始准则要求以表格形式对FLC进行定义，通过将损伤起始时的最大主应变作为最小主应变以及可选的温度和预定义的场变量的表格函数，ε FLD major (ε minor， θ， fi)。

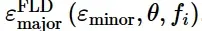
FLD的损伤起始准则为ω FLD = 1，其中变量ω FLD是当前变形状态的函数，定义为当前最大主应变εmajor与FLC上主极限应变的比值：

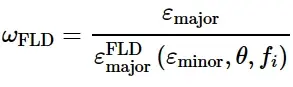
例如，对于图1中A点给出的变形状态，损伤起始判据计算为：

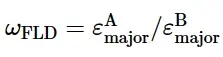
损伤起始判据

如果最小应变值在指定的表格值范围之外，Abaqus将通过假设曲线端点的斜率保持不变来外推FLC上的最大极限应变值。而关于温度和场变量的外推遵循标准约定：假设该属性在温度和场变量的指定范围之外是恒定的。

实验中，FLDs是在不受弯曲影响的情况下薄片的双轴拉伸测量的。然而，在弯曲载荷下，大多数材料可以达到比FLC上的极限应变大得多的极限应变。为了避免在弯曲变形下预测失效过早，Abaqus通过单元的厚度使用中性层平面的应变来评估FLD准则。对于具有多层的复合材料壳，在每一层的中平面面上对准则进行评估，并指定了一条FLD曲线，从而确保只考虑双轴拉伸效应。因此，FLD准则不适合模拟弯曲荷载下的破坏；其他破坏模型(如延性破坏和剪切破坏)更适合这种加载。一旦满足FLD损伤起始准则，损伤的演化在每个材料点通过基于该点局部变形的单元厚度独立进行。因此，虽然弯曲效应不影响FLD准则的评估，但它们可能会影响损伤的演化速度。

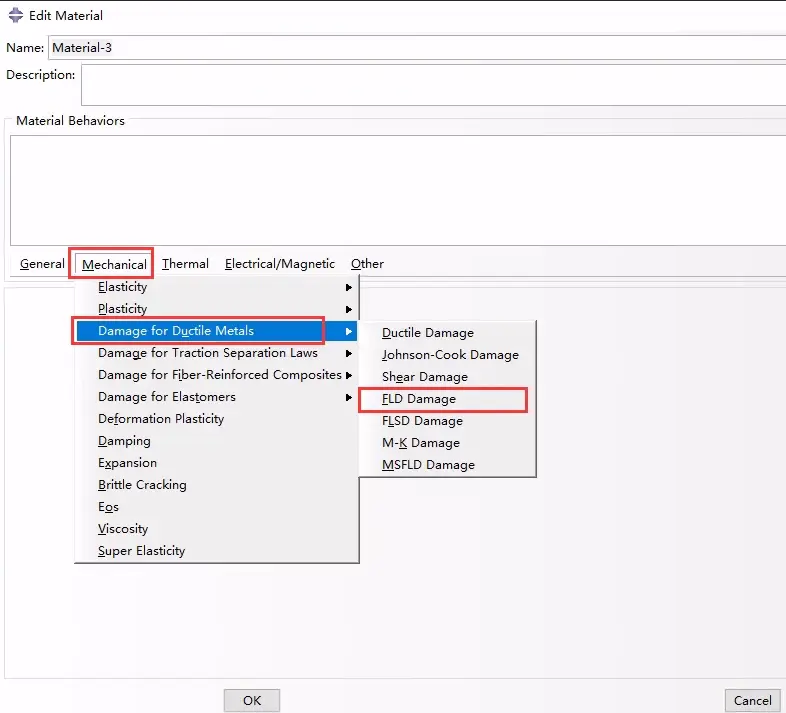
FLD损伤起始准则的CAE定义

2.2 成形极限应力图准则 Forming limit stress diagram (FLSD) criterion

当基于应变的FLC转换为基于应力的FLC时，应变路径变化对基于应力的曲线的影响最小(Stoughton, 2000)；即不同的应变FLC对应不同的应变路径，被映射到一个单一的应力FLC上。这种特性使得成形极限应力图(FLSD)成为预测任意载荷下颈缩失稳的一个有吸引力的替代方法。然而，基于应力的极限曲线在应变路径上的明显独立性可能仅仅反映了屈服应力对塑性变形变化的小敏感性。这个话题在研究界仍在讨论中。

FLSD是FLD的应力对应图，在垂直轴和水平轴上分别绘制了与颈缩局部化开始相对应的最大主面内应力和最小主面内应力。在Abaqus中，FLSD损伤起始准则要求将损伤起始时的最大主面内应力作为最小主面内应力、温度和预定义场变量(可选)的表函数进行定义。

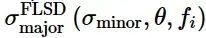
当ω FLSD = 1时满足FLSD的损伤起裂准则：

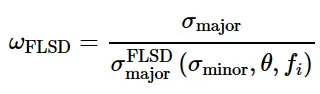
FLSD的损伤起裂准则

同样，如果最小应力值在指定的表格值范围之外，Abaqus将假设曲线端点处的斜率保持不变外推出最大极限应力的值。关于温度和场变量的外推遵循标准约定：假设该属性在温度和场变量的指定范围之外是恒定的。

由于与前面讨论的FLD准则类似的原因，Abaqus使用通过单元(或层，在多层复合壳的情况下)厚度的平均应力来评估FLSD准则，忽略了弯曲效应。因此，FLSD准则不能用于模拟弯曲荷载下的破坏；其他破坏模式(如延性破坏和剪切破坏)更适合这种加载。一旦满足FLSD损伤起始准则，则基于单元在该点的局部变形，通过单元的厚度独立驱动损伤在每个材料点的演化。因此，虽然弯曲效应不影响FLSD准则的评估，但它们可能会影响损伤的演化速度。

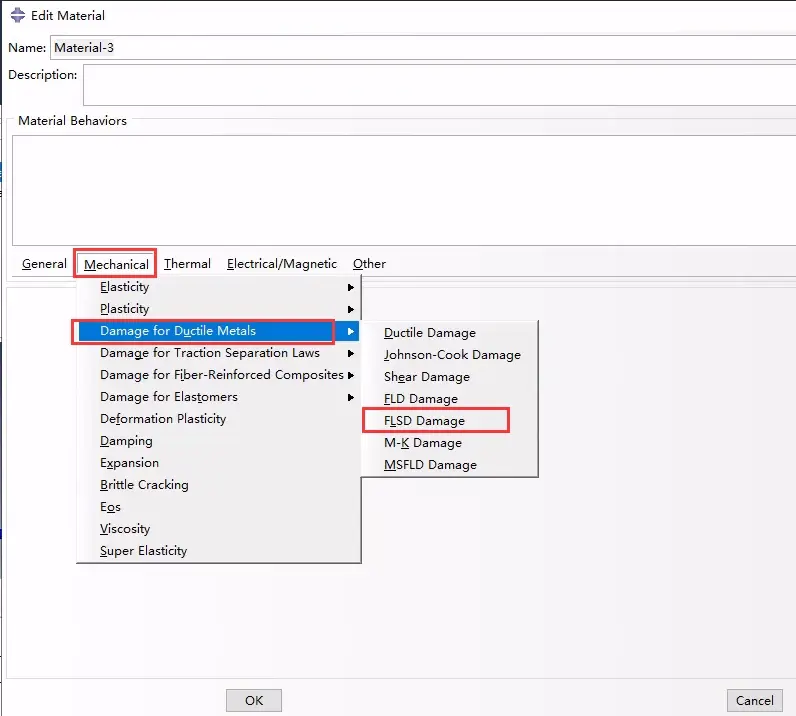
FLSD损伤起始准则的CAE定义

2.3 Marciniak-Kuczynski (M-K)起始准则 Marciniak-Kuczynski (M-K) criterion

Abaqus/Explicit中另一种准确预测任意加载路径下成形极限的方法是基于Marciniak和Kuczynski(1967)提出的局部化分析。该方法可以与Mises 和 Johnson-Cook塑性模型一起使用，包括随动硬化。在M-K分析中，虚拟厚度缺陷是作为凹槽引入的，以模拟均匀片状材料中预先存在的缺陷。在每个槽内计算由于槽外施加载荷而产生的变形场。当槽内变形相对于(槽外)标称变形的比率大于临界值时，认为发生颈缩。

图2显示了用于M-K分析的槽的几何形状示意图。图中a为缺陷外的壳单元标称区域，b为弱的槽区域。缺陷相对于公称厚度的初始厚度由比值给出：

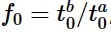
下标0表示初始无应变状态下的量。

所述槽相对于所述局部材料取向的1个方向定向为零角。

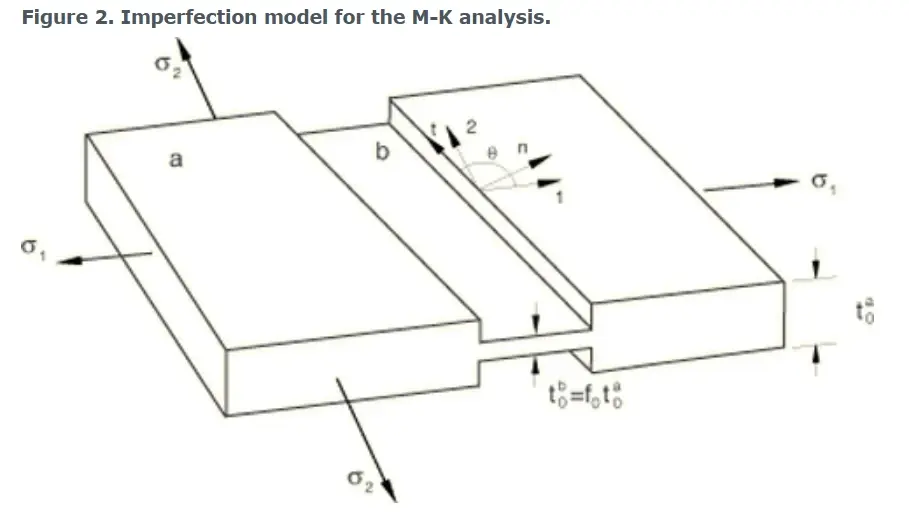
图2 M-K分析的缺陷模型

Abaqus/Explicit允许指定厚度缺陷的各向异性分布，作为相对于局部材料方向的角度函数，f0(θ)。Abaqus/Explicit首先求解名义区域内的应力-应变场，忽略缺陷的存在；然后单独考虑每个槽的作用。通过施加应变协调条件，计算了各槽内的变形场：

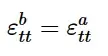
应变协调条件

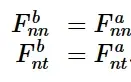
力的平衡方程

下标n和t表示与凹槽法向和切向的方向。在上述平衡方程中，F n n和F n t是在t方向上每单位宽度的力。

颈缩不稳定假定当槽内的变形率相对于非槽处的变形率之比大于临界值时发生。此外，草的局部化也可能导致无法找到满足平衡和相容性条件的解；因此，未能找到收敛的解决方案也是局部颈缩开始的一个指标。对于损伤起始准则的评估，Abaqus/Explicit使用以下变形严重程度度量：

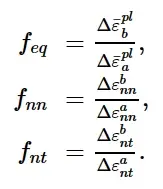
在每个指定的槽方向上对这些变形严重系数进行了评估，并与临界值进行了比较。(仅当增量变形主要为塑性变形时才进行评估；如果变形增量是弹性的，则M-K准则不能预测损伤起始。)采用最不利的槽口方向进行损伤起裂的判据，计算公式为：

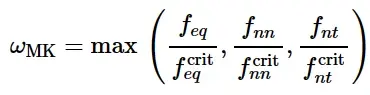
MK损伤起裂判据

其中，f crit eq、f crit nn、f crit nt为变形严重程度指标的临界值。当ω MK = 1或无法找到平衡方程和相容性方程的收敛解时，损伤发生。默认情况下，Abaqus/Explicit假设f crit eq = f crit nn = f crit nt = 10，也可以指定不同的值。如果将其中一个参数设为零，则其对应的变形严重系数不计入损伤起始准则的评定。如果所有这些参数都设为零，则M-K准则仅用于评估基于平衡方程和相容方程的非收敛性。

必须指定f0，等于虚拟缺陷处的初始厚度除以标称厚度(见图2)，以及用于评估M-K损伤起始准则的缺陷数量。假定这些方向在角度上间隔相等。默认情况下，Abaqus/Explicit使用四个缺陷，分别位于0°，45°，90°和135°，相对于材料的局部1方向。初始缺陷尺寸可定义为角方向的表格函数，f0 (θ)，从而允许对材料中缺陷的各向异性分布进行建模。Abaqus/Explicit将使用此表来评估每个缺陷的厚度，这些缺陷将用于M-K分析方法的评估。此外，初始缺陷尺寸也可以是初始温度和场变量的函数;这允许定义不完美的非均匀空间分布。Abaqus/Explicit将在分析开始时根据温度和场变量的值计算初始缺陷大小。在接下来的分析中，缺陷的初始尺寸保持不变。

一般建议选择f0的值，使单轴应变加载条件下(ε minor = 0)的数值预测的成形极限与实验结果相匹配。引入虚拟槽来评估颈缩失稳的发生;它们不影响底层单元的结果。一旦满足颈缩失稳准则，构件内的材料性能就会按照规定的损伤演化规律退化。

MK损伤起始准则的CAE定义位置

M-K准则的性能考虑：

当使用M-K准则时，总体计算成本可能会大幅增加。例如，与没有M-K准则的成本相比，加工具有三个截面点的壳单元的成本增加了大约两倍，这是M-K准则的默认值。您可以通过减少所考虑的缺陷方向的数量或通过增加M-K计算之间的增量数量来减轻评估该损伤起始准则的成本，如下所述。当然，对整体分析成本的影响取决于模型中使用该损伤起裂准则的单元的比例。在M-K准则下，每个单元的计算成本大约增加了一个因子：

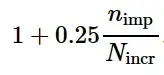
其中n imp是为M-K准则的评估指定的缺陷数，N incr是执行M-K计算的频率，以增量为单位。在大多数情况下，上述公式中的系数0.25给出了对成本增加的合理估计，但实际成本增加可能与此估计不同。默认情况下，Abaqus/Explicit在每个时间增量上对每个缺陷执行M-K计算，N incr = 1。必须注意确保频繁地进行M-K计算，以确保每个缺陷上的变形场的精确积分。

2.4 Müschenborn-Sonne forming limit diagram (MSFLD) criterion

Müschenborn和Sonne(1975)提出了一种基于等效塑性应变来预测变形路径对板料成形极限影响的方法，该方法假设成形极限曲线代表可达到的最高等效塑性应变之和。Abaqus利用这一思想的推广，建立了任意变形路径下金属板颈缩失稳判据。该方法要求将原始成形极限曲线(无预变形效应)从最大应变与最小应变的空间转变为等效塑性应变¯ε pl的空间与主应变率之比α =˙ε minor /˙ε major。

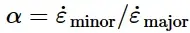
对于线性应变路径，假设塑性不可压缩，忽略弹性应变:

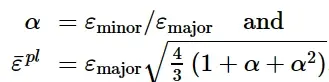
如图3所示，FLD中的线性变形路径转换为¯ε pl - α图中的垂直路径(α值恒定)。

图3

根据MSFLD准则，当¯ε p - α图中的变形状态序列与成形极限曲线相交时，局部颈缩发生，如下所述。强调的是，对于线性变形路径，FLD和MSFLD表示是相同的，并产生相同的预测。然而，对于任意载荷，MSFLD表示通过使用累积等效塑性应变来考虑变形历史的影响。

为了在Abaqus中使用MSFLD损伤起始准则时，可以直接提供损伤起始时的等效塑性应变作为α以及可选的等效塑性应变率、温度和预定义的场变量的表格函数：

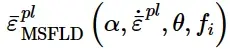
或者，也可以通过提供表的表格函数，以传统的FLD格式(在最大应变和最小应变空间中)指定曲线：在这种情况下，Abaqus将自动将数据转换为¯ε p1 - α格式。

设ω MSFLD表示当前等效塑性应变¯ε p1与极限曲线上的等效塑性应变之比：

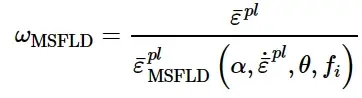
当ω MSFLD = 1满足条件时，满足颈缩失稳的MSFLD判据。如果由于应变方向的突然改变而导致¯ε p1 - α图中的变形状态序列与极限曲线相交，也会发生颈缩失稳。这种情况如图4所示。当α从α t变为α t + Δ t时，ε p1 - α图中相应点的连线与成形极限曲线相交。当这种情况发生时，达到MSFLD标准，尽管满足：

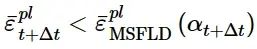
同时出于输出目的，Abaqus将ω MSFLD的值设置为1，以表示满足标准。

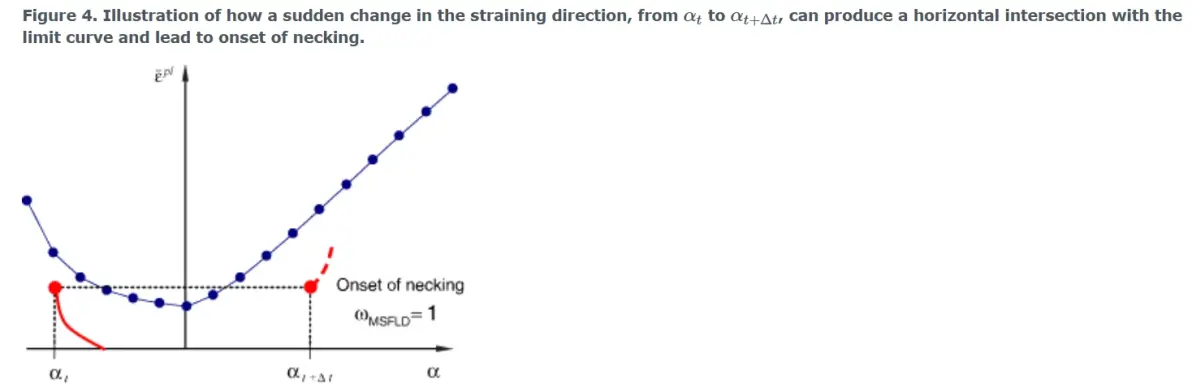
图4

在Abaqus中用于评估MSFLD准则的等效塑性应变¯ε p1仅累积在导致单元面积增加的增量上。与单元面积减少相关的应变增量不能引起颈缩，也不能对MSFLD标准的评估做出贡献。

如果α值超出指定的表格值范围，则假设曲线端点处的斜率保持不变，Abaqus外推等效塑性应变值。关于应变率、温度和场变量的外推遵循标准惯例：假设在应变率、温度和场变量的指定范围之外，该特性是恒定的。

基于MSFLD准则的颈缩失稳预测与基于Marciniak和Kuczynski准则的预测非常吻合，计算成本明显低于Marciniak和Kuczynski准则。然而，在某些情况下，MSFLD准则可能会高估材料中剩余的可成形性。这种情况发生在加载过程中的某个时候，材料达到非常接近颈缩不稳定点的状态，并随后在可以承受进一步变形的方向上进行应变。在这种情况下，MSFLD准则预测新方向上的额外成形性量大于Marciniak和Kuczynski准则预测的量。然而，在实际的成形应用中，这种情况通常不是一个问题，因为通常使用成形极限图中的安全系数来确保材料状态离颈缩点足够远。

由于与前面讨论的FLD准则类似的原因，Abaqus使用通过单元(或层，在多层复合壳的情况下)厚度的中层应变来评估MSFLD准则，忽略弯曲效应。因此，MSFLD准则不能用于模拟弯曲荷载下的破坏；其他破坏模式(如延性破坏和剪切破坏)更适合这种加载。一旦满足MSFLD损伤起裂准则，基于该点局部变形的单元厚度，在每个材料点独立驱动损伤演化。因此，虽然弯曲效应不影响MSFLD准则的评估，但它们可能会影响损伤的演化速度。

MSFLD损伤起始标准的CAE定义位置

主应变率比的数值计算：

主应变率的比值α =˙εminor/˙εmajor，会因变形路径的突然变化而出现跳变。在显式动态模拟过程中，需要特别注意避免由数值噪声引起的α的非物理跳跃，这可能导致变形状态与成形极限曲线的水平相交，从而导致颈缩不稳定的过早预测。

为了克服这个问题，Abaqus/Explicit不是将α计算为瞬时应变率的比率，而是根据等效塑性应变发生微小但显著变化后的累积应变增量定期更新α。触发α更新的等效塑性应变变化的阈值记为(Δ¯ε pl)∗，α近似为:

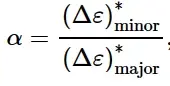
其中(Δ ε)∗minor和(Δ ε)∗major是自上次更新α以来累积塑性应变的主值。(Δ¯ε pl)∗的默认值为0.002(0.2%)，且不能在Abaqus/CAE中直接指定。

此外，Abaqus/Explicit还支持以下方法来计算α：

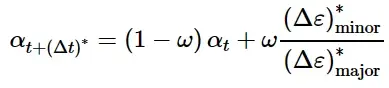
其中(Δ t)∗表示使等效塑性应变增加至少(Δ¯ε pl)∗所需的分析增量上的累积时间。因子ω (0 <ω≤1)有利于滤波高频振荡。如果使用适当的值(Δ¯ε pl)∗，则通常不需要这种滤波方法。可以直接指定ω的值。缺省值为ω = 1.0(无滤波)。

在Abaqus/Standard中，α在每个分析增量处计算为α t + Δ t = Δ ε minor / Δ ε major，而不使用上述任何一种过滤方法。但是，仍然可以指定值(Δ¯ε p l)∗和ω；这些值可以导入到Abaqus/Explicit中的任何后续分析中。

指定ω

初始条件：

当我们需要研究材料先前遭受变形的行为时，例如在制造过程中产生的变形，可以提供初始等效塑性应变值来指定材料的初始工作硬化状态。

此外，当初始等效塑性应变大于成形极限曲线上的最小值时，α的初始值对后续变形是否满足MSFLD损伤起裂准则起着重要作用。因此，在这些情况下指定α的初始值是很重要的。为此，可以指定塑性应变张量的初值。Abaqus将利用这些信息计算α的初始值，即最大，最小主塑性应变之比；即忽略变形的弹性分量，假设变形路径为线性。

3. 单元和输出

除了Abaqus/Explicit中的管道单元外，塑性金属损伤起裂准则可用于Abaqus中包含力学行为(具有位移自由度的单元)的任何单元。

金属板颈失稳模型(FLD、FLSD、MSFLD和M-K)仅适用于包含力学行为的单元，并使用平面应力公式(即平面应力、壳、连续壳和膜单元)。

除了Abaqus中可用的标准输出标识符外，当指定损伤起始准则时，以下变量具有特殊含义:

ERPRATIO: 主应变率之比，α，用于MSFLD损伤起始准则。

SHRRATIO：剪应力比θ s = (q + ks p) / τ max，用于评价剪切损伤起裂准则。

TRIAX：应力三轴度，η = - p / q(仅在Abaqus/Standard中与损伤起裂有关)。

DMICRT：所有损伤起始标准的分量如下所列。

DUCTCRT：延性损伤起始准则，ω D。

JCCRT：Johnson-Cook损伤起始准则(仅在Abaqus/Explicit中可用)。

SHRCRT：剪切损伤起始准则，ω S。

FLDCRT：分析过程中FLD损伤起始准则的最大值，ω FLD。