Abaqus渐进损伤与失效（2.3）：延性金属的损伤演化与单元删除

感觉很多人都放假了哈~祝大家假期愉快，龙年吉祥！我们没放假的接着学哈~

延性金属的损伤演化能力：

假设损伤的特征是材料刚度的逐步退化，导致材料失效；

必须与延性金属的损伤起裂准则结合使用；

使用与网格无关的量(塑性位移或能量耗散)来描述损伤开始后的损伤演变；

考虑到同时作用于同一材料的不同损伤机制的综合影响，并包括指定每种机制如何促进整体材料退化的选项；

提供失效发生时的选项，包括从网格中移除单元。

1. 损伤演化

图1显示了材料遭受损伤时的典型应力-应变行为。在具有各向同性硬化的弹塑性材料中，损伤表现为屈服应力软化和弹性退化两种形式。图中实线为损伤后的应力-应变响应，虚线为无损伤时的响应。正如后面讨论的那样，损伤的响应取决于单元的尺寸，应使结果的网格依赖性最小化。

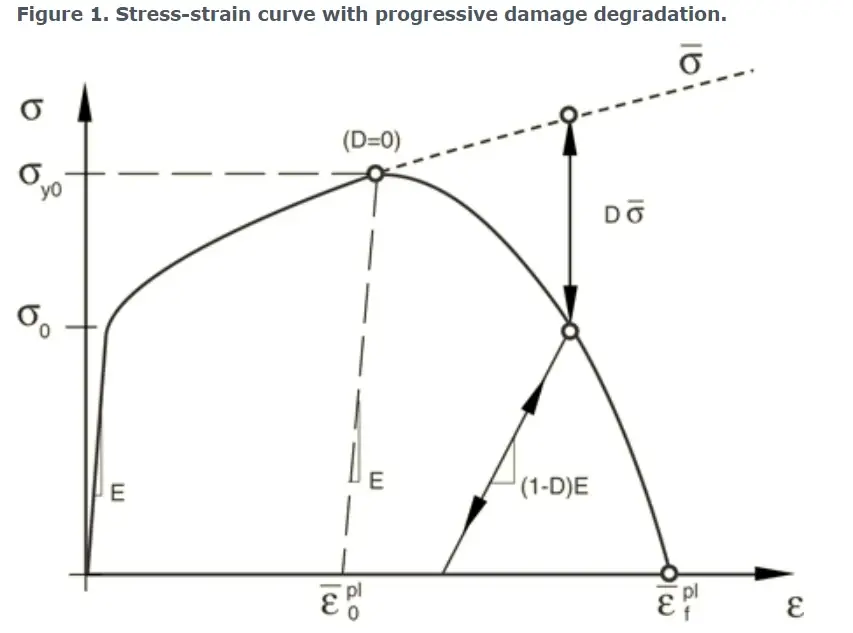
图1 渐进损伤退化的应力-应变曲线

图中σ y0和¯ε pl 0为损伤起始时的屈服应力和等效塑性应变，¯ε pl f为当整体损伤变量达到D = 1时，破坏时的等效塑性应变。整体损伤变量D捕获了所有主动损伤机制的综合效果，并根据每个损伤变量Di进行计算。

失效时等效塑性应变的值¯ε pl f取决于单元的特征长度，不能作为描述损伤演化规律的材料参数。因此损伤演化规律用等效塑性位移(¯u pl)或断裂能量耗散(G f)来表示。

1.1 网格依赖性和特征长度

当材料发生损伤时，应力应变关系不再准确地代表材料的行为。继续使用引入了基于应变局部化的强网格依赖性的应力-应变关系，使得随着网格的细化，能量耗散减少。需要采用不同的方法来遵循应力-应变响应曲线的应变软化分支。Hillerborg(1976)的断裂能建议在损伤开始后通过产生应力-位移响应来减少网格依赖。Hillerborg利用脆性断裂的概念，将打开单位面积裂纹所需的能量Gf定义为材料参数。使用这种方法，损伤开始后的软化响应的特征是应力-位移响应而不是应力-应变响应。

在有限元模型中实现这种应力-位移概念需要定义与积分点相关的特征长度L。断裂能为：

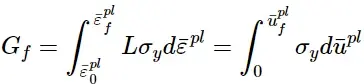
该表达式引入了等效塑性位移的定义¯u pl，作为损伤发生后屈服应力的断裂功共轭(每单位面积的断裂功)。损伤发生前：

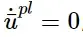
损伤发生后：

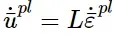
特征长度的定义取决于单元的几何形状和公式：对于一阶单元，它是穿过单元的一条线的典型长度；它是二阶单元相同典型长度的一半。对于梁和桁架，它是沿单元轴的特征长度。对于膜和壳，它是参考面的特征长度。对于轴对称单元，它只是r-z平面上的特征长度。对于粘聚力单元，它等于本构厚度。之所以使用这种特征长度的定义，是因为断裂发生的方向事先是未知的。因此，具有大宽高比的单元将具有相当不同的行为，这取决于它们破裂的方向：由于这种影响，一些网格敏感性仍然存在，并且建议单元应具有接近统一的宽高比。或者，可以通过在用户子程序VUCHARLENGTH中直接指定特征长度作为单元拓扑和材料方向的函数来减少这种网格依赖性。

在损伤起裂中描述的每一种损伤起始准则可能拥有相关的损伤演化规律。损伤演化规律可以用等效塑性位移(¯u pl)或断裂能量耗散(Gf)来表示。这两种选择都考虑了单元的特征长度，以减轻结果对网格的依赖。

1.2 多个起始准则时评估整体的损伤

整体损伤变量D捕获了所有起始准则的综合效果，并根据每个准则的单个损伤变量di 进行计算。可以选择将一部分损伤变量以乘法的方式组合成一个中间变量dmult，如下所示：

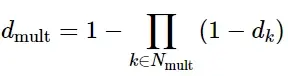
然后，将整体损伤变量计算为dmult与其余损伤变量的最大值：

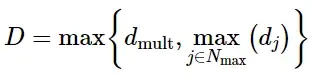
整体损伤变量

在上述表达式中，N mult和N max分别表示在乘法和最大值意义上造成整体损伤的主动机制集合，其中N act = N mult∪N max。

使用以下操作分别指定与特定损伤起始准则相关的损伤在最大值(默认)或乘法意义上对总体损伤变量的贡献：

Property module: material editor: MechanicalDamage for Ductile Metalscriterion: SuboptionsDamage Evolution: Degradation:Maximum or Multiplicative

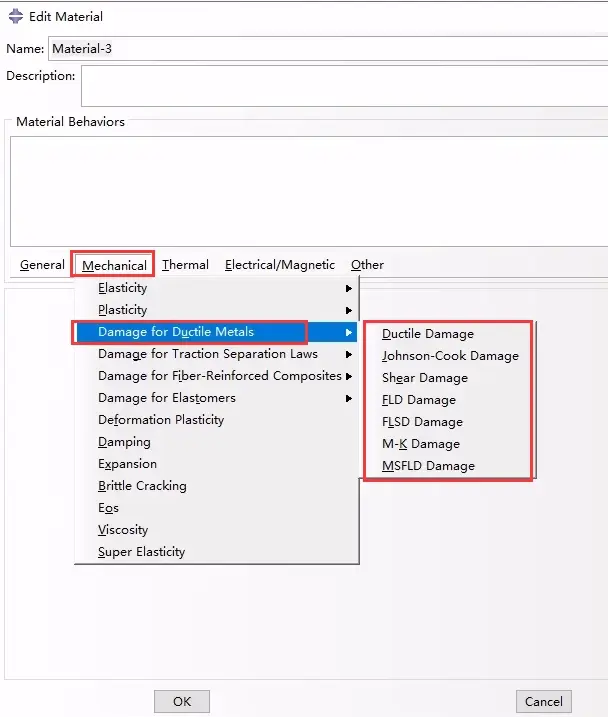
选择损伤起始准则

子选项：损伤演化

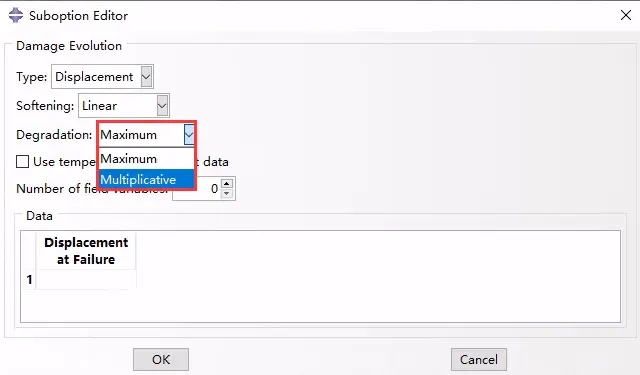
最大值或者乘法

2. 基于有效塑性位移定义损伤演化

如前所述，一旦达到损伤起始准则，则用演化方程定义有效塑性位移¯u pl：

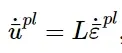
effective plastic displacement,式中L为单元的特征长度。

损伤变量随相对塑性位移的演变可以用表格、线性或指数形式表示。当失效时的塑性位移(¯u pl f)为0时，将发生瞬时破坏；但是，不推荐这种选择，应该谨慎使用，因为它会导致材料点的应力突然下降，从而导致动态不稳定。

表格的形式：

可以将损伤变量直接指定为等效塑性位移的表格函数d = d(¯u pl)，如图2(a)所示。

图2a 损伤变量定义为等效塑性位移的表格形式

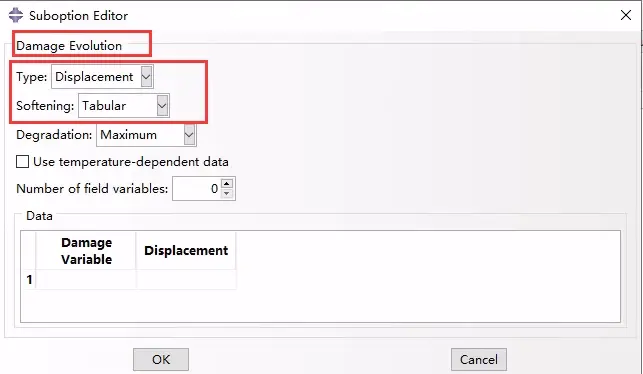
在CAE定义中的选择

线性的形式：

假设损伤变量随有效塑性位移线性演化，如图2(b)所示。

图2b

则可以指定失效点(完全退化)的有效塑性位移，¯u pl f。然后，损伤变量：

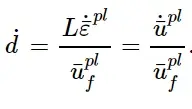
此定义保证了当有效塑性位移达到¯u pl =¯u pl f时，材料刚度完全退化(d = 1)。当材料在损伤发生后的有效响应为理想塑性(屈服应力恒定)时，线性损伤演化规律定义了真正的线性应力-应变软化响应。

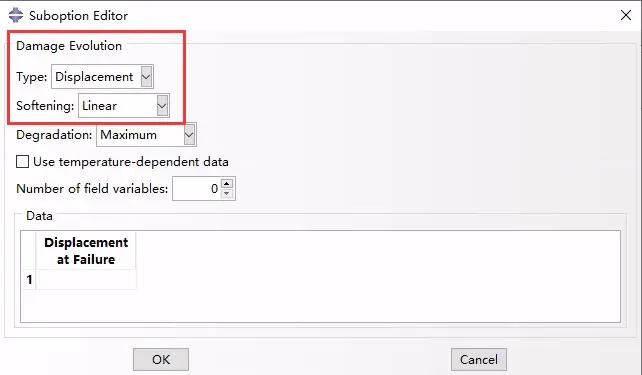
在CAE中的定义选项

指数的形式：

假设损伤变量随塑性位移呈指数演化，如图2(c)所示。

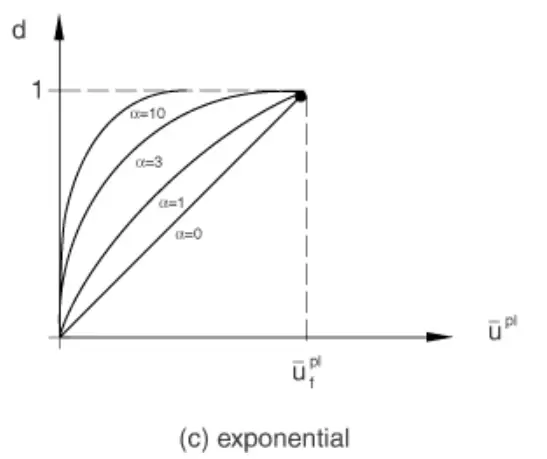
图2c

则可以指定失效时的相对塑性位移，¯u pl f 和指数 α。损伤变量为：

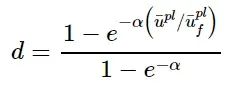
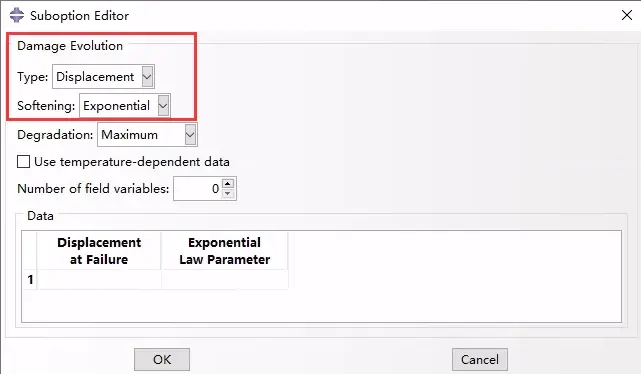
在CAE中的选项

3. 基于损伤过程中能量耗散来定义损伤演化

可以直接指定在损伤过程中每单位面积的断裂能Gf。若Gf为0，则会发生瞬时失效。但是，不推荐这种选择，应该谨慎使用，因为它会导致材料点的应力突然下降，从而导致动态不稳定。

损伤的演化可以用线性或指数形式来表示。

线性的形式：

假设损伤变量随塑性位移呈线性演化。则可以指定单位面积的断裂能，Gf。然后，一旦满足损伤起始准则，损伤变量将根据下式增加：

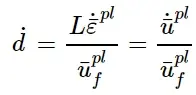
与基于位移的一致

其中失效时的等效塑性位移计算为：

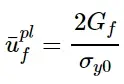
σ y0为达到起始准则时的屈服应力值。

因此，该模型与图2(b)中所示的模型等效。该模型保证在损伤发生后材料的有效响应为理想塑性(恒定屈服应力)时，损伤演化过程中耗散的能量等于Gf。

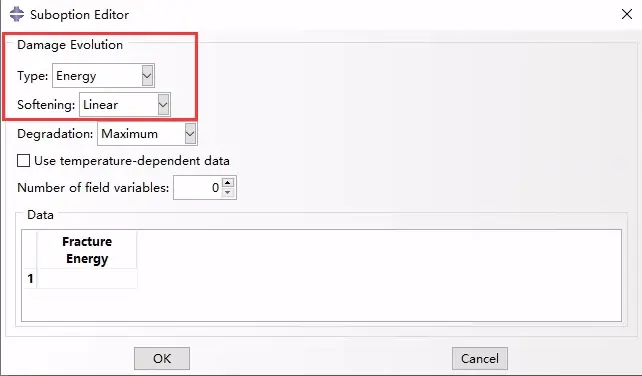
CAE中的定义

指数的形式：

假设损伤变量的指数演化为;

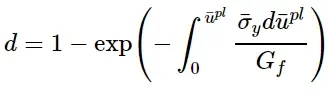
公式保证了损伤演化过程中耗散的能量等于Gf，如图3(a)所示。理论上，损伤变量在等效塑性位移趋于无穷时才渐近达到1(图3 (b))。

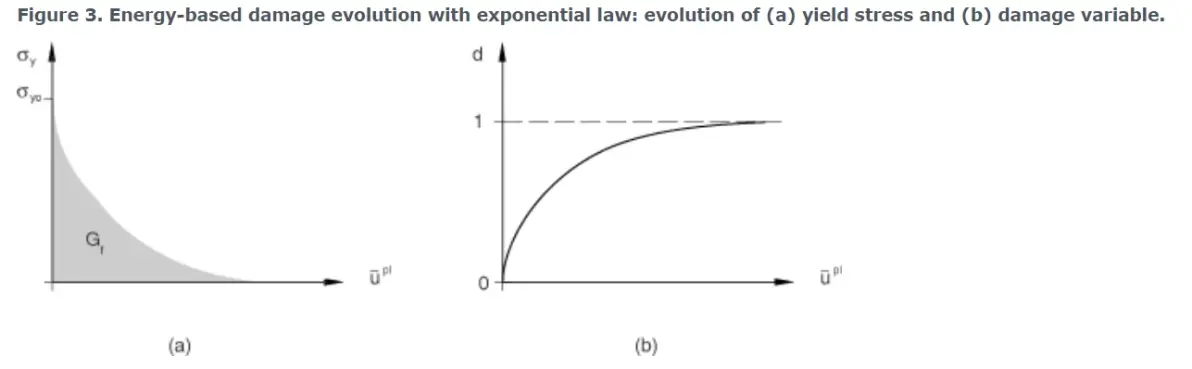
图3 基于能量的指数型损伤演化:(a)屈服应力与(b)损伤变量的演化

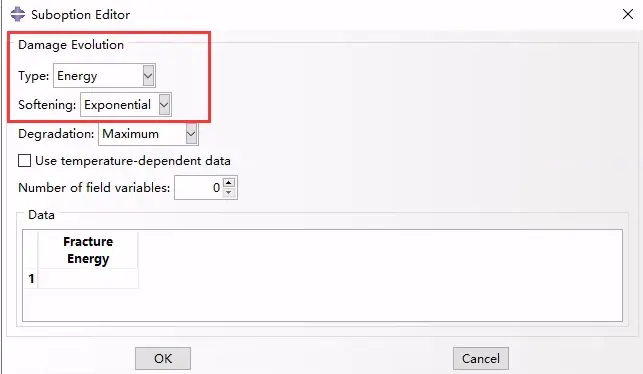
CAE中的指定

4. 最大刚度退化和选择单元删除

可以控制Abaqus如何处理具有严重损伤的单元。可以为整体损伤变量D指定一个上限，Dmax;或者可以选择是否在达到最大刚度退化时删除某个单元。

4.1 指定最大刚度退化值

Dmax取决于是否要在达到最大退化时删除单元。对于默认情况单元删除和所有粘聚力单元的情况，Dmax = 1.0；否则Dmax = 0.99。输出变量SDEG包含D的值。 一旦D达到Dmax，积分点便不会进一步的损伤积累(除了在删除单元时失去任何剩余的刚度)。

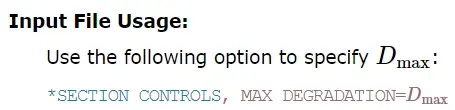
通过输入文件指定

4.2 从网格中删除单元

单元在达到最大退化时默认被删除。除了具有牵引分离响应的粘聚力单元，Abaqus对最终可能被删除的单元的所有刚度分量平等地施加损伤：

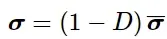
在Abaqus/Standard中，除了粘聚力单元外，如果在单元的所有积分点处的所有截面点上D都达到Dmax，则从网格中删除该单元(而对于粘聚力单元，删除单元的条件是D在所有积分点上都达到Dmax，对于牵引分离响应，没有一个积分点处于压缩状态)。

在Abaqus/Explicit中，除粘聚力单元外，如果在单元的任何一个积分点处的所有截面点上D都达到Dmax，则从网格中删除单元(对于粘聚力单元，删除单元的条件是D在所有积分点上都达到Dmax，对于牵引分离响应，没有一个积分点处于压缩状态)。例如，在默认情况下，任何一个积分点达到最大降解时将发生实体单元的移除。然而，在壳单元中，在单元从网格中移除之前，单元的任何一个积分点处的所有贯穿厚度截面点都必须失效。在二阶减缩积分梁单元的情况下，通过沿梁轴的两个单元积分点处的任意一个的厚度在所有截面点达到最大退化，默认情况下导致单元移除。同样，在改进的三角形和四面体实体单元和完全积分的膜单元中，D在任意一个集分点达到Dmax，默认会导致单元移除。

在传热分析中，材料的热性能不受材料刚度的渐进损伤的影响，直到达到单元删除的条件；单元删除后，单元的热贡献也被消除了。

输入文件中默认使用单元删除

4.3 在计算中保留单元

除了三维梁单元，也可以选择不从网格中移除单元。当单元删除关闭时，整体损伤变量强制为D≤Dmax。如果单元删除被关闭，默认值是Dmax = 0.99，这将确保单元在模拟中保持有效，剩余刚度至少为原始刚度的1%。在传热分析中，材料的热性能不受材料刚度损伤的影响。

通过输入文件修改为不使用单元删除

在Abaqus/Explicit中具有三维应力状态的单元：

对于具有三维应力状态的单元(包括广义平面应变单元)，剪切刚度将退化到最大值Dmax，导致偏应力分量软化。然而，只有当材料受到负压(即静水压力)时，体刚度才会下降；在正压力下没有体积退化。这对应于类似流体的行为。因此，退化偏差S和压力p应力计算为：

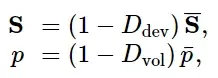
其中，偏差和体积损伤变量为：

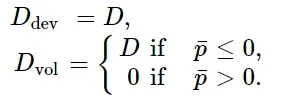
在这种情况下，输出变量SDEG包含D dev的值。

在Abaqus/Standard中具有三维应力状态的单元：

对于具有三维应力状态的单元(包括广义平面应变单元)，刚度将均匀退化，直至达到最大退化D max。输出变量SDEG包含D的值。

具有平面应力状态的单元：

对于具有平面应力公式的单元(平面应力、壳单元、连续壳单元和膜单元)，刚度将均匀退化，直到达到最大退化D max。输出变量SDEG包含D的值。

具有一维应力状态的单元：

对于具有一维应力状态的单元(即，桁架单元，钢筋和具有垫片行为的粘性单元)，如果其唯一的应力分量为正(张力)，则会退化。材料的刚度在压缩载荷下不受影响。因此，应力由σ =(1−D uni)¯σ给出，其中单轴损伤变量计算为：

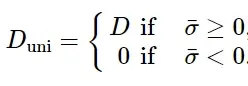
在这种情况下，D max决定了单轴拉伸的最大允许退化(D≤D max)。输出变量SDEG包含D单位的值。

5. Abaqus/Standard中的收敛困难

在Abaqus/Standard等隐式分析程序中，表现出软化行为和刚度退化的材料模型经常导致严重的收敛困难。在Abaqus/Standard中提供了一些技术来提高涉及这些材料的分析的收敛性。

Abaqus/Standard中的粘性正则化：

通过使用粘性正则化方案，可以克服与软化和刚度退化相关的一些收敛困难，这使得软化材料的正切刚度矩阵在足够小的时间增量内为正。

在此正则化方案中，粘性损伤变量定义为演化方程：

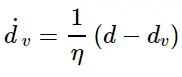
其中η是表示粘性系统松弛时间的粘性系数，d是在无粘基础模型中评估的损伤变量。利用损伤变量的粘性值计算粘性材料的损伤响应。使用较小的粘性参数值(与特征时间增量相比较小)的粘性正则化通常有助于提高模型在软化状态下的收敛速度，而不会影响结果。基本思想是粘性系统的解松弛为t / η→∞，其中t表示时间。

非对称方程求解器：

一般情况下，采用任何一种延性演化模型，材料雅可比矩阵都是非对称的。为了提高收敛性，建议在这种情况下使用非对称方程求解器。

6. 采用钢筋损伤模型

除非损伤也包括在钢筋材料定义中，否则钢筋对构件承载应力能力的贡献不会受到影响；在钢筋达到规定的损伤起裂标准后，钢筋对构件承载应力的贡献也会降低。对于单元删除的默认选择，在任何一个积分点位置，基础材料和钢筋中的所有截面点完全退化时，单元从网格中移除。

7. 单元和输出

可以用于定义延性金属损伤起始准则的所有单元。

除了Abaqus中可用的标准输出标识符外，当指定损伤演化时，以下变量具有特殊含义:

STATUS： 单元的状态(如果单元有效，状态是1.0，如果元素失效，状态是0.0)

SDEG：总体标量刚度退化，D

说明：本系列文章是up主边学边整理的，可以看作是学习笔记，存在的错误欢迎指出。

如果对你有帮助，请一键三连吧~关注up主，学习不迷路~

欢迎评论区交流讨论~