LS最小二乘法数据拟合Matlab仿真实验

1.算法描述

最小均方算法，简称LMS算法，是一种最陡下降算法的改进算法， 是在维纳滤波理论上运用速下降法后的优化延伸，最早是由 Widrow 和 Hoff 提出来的。 该算法不需要已知输入信号和期望信号的统计特征，“当前时刻”的权系数是通过“上一 时刻”权系数再加上一个负均方误差梯度的比例项求得。 其具有计算复杂程度低、在信号为平稳信号的环境中收敛性好、其期望值无偏地收敛到维纳解和利用有限精度实现算法时的平稳性等特性，使LMS算法成为自适应算法中稳定性最好、应用最广的算法。

根据小均方误差准则以及均方误差曲面，自然的我们会想到沿每一时刻均方误差的陡下降在权向量面上的投影方向更新，
也就是通过目标函数ξ（k）的反梯度向量来反复迭代更新。由于均方误差性能曲面只有一个极小值，只要收敛步长选择恰当，
不管初始权向量在哪，后都可以收敛到误差曲面的小点，或者是在它的一个邻域内。这种沿目标函数梯度反方向来解决小化问题的方法，
我们一般称为速下降法，表达式如下：

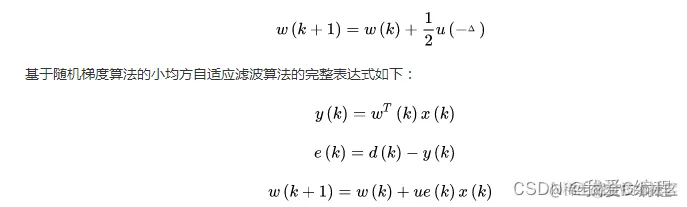
假设有一组实验数据（xi, yi），事先知道它们之间应该满足某函数关系yi = f(xi)，通过这些已知的信息，需要确定函数f的一些参数。例如，
如果函数f是线性函数f(x) = kx + b，那么参数k和b就是需要确定的值。

如果用p表示函数中需要确定的参数，那么目标就是找到一组p，使下面的函数s的值最小：

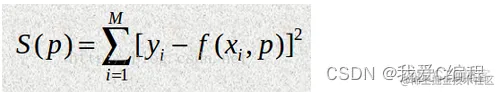
这种算法被称作最小二乘拟合(Least-square fitting)。

2.仿真效果预览

matlab2022a仿真结果如下：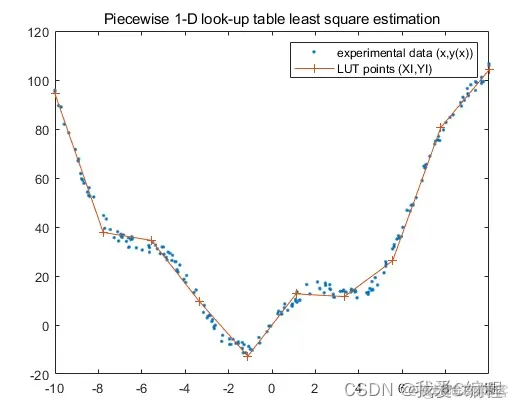

3.MATLAB核心程序

clear;
close all;
warning off;
addpath(genpath(pwd));
 
x = [-10:0.1:10]';
x = x+2*(rand(size(x))-0.5);
x = max(min(x,10),-10);
y = x+x.^2+10*sin(x)+5*(rand(size(x))-0.5);
XI = linspace(min(x),max(x),10);
YI = lsq_lut_piecewise( x, y, XI );
plot(x,y,'.',XI,YI,'+-')
legend('experimental data (x,y(x))','LUT points (XI,YI)')
title('Piecewise 1-D look-up table least square estimation')

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删