产品
原理请参考:李庆杨 《数值分析》,3.4节曲线拟合的最小二乘法。
classdef LSPolynomialCurveFitting < handle
% 多项式曲线拟合,线性最小二乘拟合同样适用, k 阶次为 1 即可。
properties(Access=private)
x % 自变量
y % 因变量
k % 最高拟合阶次
fit_poly %曲线拟合的多项式
poly_coefficient % 曲线拟合多项式的系数
end
methods(Access=public)
% 构造函数
function self = LSPolynomialCurveFitting(x, y, k)
self.x = x; % 自变量数据向量
self.y = y; % 自变量数据向量
self.k = k; % 最高拟合的阶次
if length(x) ~= length(y)
error("拟合数据的长度不匹配!")
end
end
%% 多项式拟合核心算法
function sol = fit(self)
c = zeros(2 * self.k + 1, 1); % 系数矩阵2n+1个不同的值
b = zeros(self.k + 1, 1); % 右端向量
for i = 0 : 2 * self.k
c(i + 1) = sum(power(self.x, i));
if i < self.k + 1
b(i + 1) = dot(self.y, power(self.x, i));
end
end
C = zeros(self.k + 1, self.k + 1); % 构造对称正定系数矩阵
C(1, :) = c(1:self.k + 1);
for i = 2:self.k + 1
C(i, :) = c(i:self.k + i);
end
self.poly_coefficient = C \ b; % 解方程组获得系数
sol.C = C;
sol.b = b;
sol.coefficient = self.poly_coefficient;
sol.fit_poly = vpa(self.create_poly()); % 构造拟合的多项式
[sol.fit_error, sol.mse] = self.error_analysis(); % 误差分析
end
%% 计算给定值的拟合多项式的值
function y0 = predict(self, x0)
f_poly = matlabFunction(self.fit_poly);
y0 = f_poly(x0);
end
%% 可视化插值多项式
function plt_polynomial(self)
xi = linspace(min(self.x), max(self.x), 100);
f_poly = matlabFunction(self.fit_poly); % 符号函数转化为匿名函数
yi = f_poly(xi);
plot(xi, yi, "-", "LineWidth", 1.5)
hold on
plot(self.x, self.y, "o", "MarkerFaceColor","k", "MarkerEdgeColor", "k")
grid on; grid minor; box off; hold off
xlabel("$x$", "Interpreter","latex")
ylabel("$f(x)$", Interpreter="latex")
title("最小二乘多项式曲线拟合与拟合点图形")
end
end
methods(Access=private)
%% 构造拟合的多项式
function fit_poly = create_poly(self)
syms t
fit_poly = self.poly_coefficient(1) * 1; % 常数项
for i = 1 : self.k
px = power(t, i); % i次幂项
fit_poly = fit_poly + self.poly_coefficient(i + 1) * px;
end
self.fit_poly = fit_poly;
end
%% 误差分析
function [fit_error, mse] = error_analysis(self)
y_hat = self.predict(self.x);
fit_error = self.y - y_hat; % 误差
mse = mean(fit_error .^ 2); % 均方误差
end
end
end测试案例
例1:以自定义的多项式测试算法拟合的系数的正确性。
>> x = 0:0.05:5;
>> y = 0.5 * x.^3 + 2.0 * x.^2 - 1.5 * x + 2.5;
>> lspcf = LSPolynomialCurveFitting(x, y, 3);
>> sol = lspcf.fit()
sol =
包含以下字段的 struct:
C: [4×4 double]
b: [4×1 double]
coefficient: [4×1 double]
fit_poly: 0.5*t^3 + 1.9999999999998596678096873802133*t^2 - 1.4999999999996689314940567783196*t + 2.4999999999998236965836895251414
fit_error: [1.7586e-13 1.5987e-13 1.4388e-13 1.2923e-13 1.1502e-13 1.0170e-13 8.9262e-14 7.7272e-14 6.5725e-14 5.5067e-14 4.5297e-14 … ]
mse: 6.3045e-25
>> sol.coefficient
ans =
2.5000
-1.5000
2.0000
0.5000可见,算法在功能上是正确的。如果添加一定的噪声,结果如下,与实际系数存在一定的差异,但是在最小二乘意义下是最优的。
> y = 0.5 * x.^3 + 2.0 * x.^2 - 1.5 * x + 2.5 + 0.1 * randn(1, length(x));
>> lspcf = LSPolynomialCurveFitting(x, y, 3);
>> sol = lspcf.fit();
>> sol.coefficient
ans =
2.5824
-1.5800
2.0266
0.4971例2. 以函数为例等距划分
个数据点,以此数据拟合多项式曲线。
clc, clear, close all
x = linspace(-1, 1, 20);
y = @(x)1 ./ (1 + 25 * x.^2);
% x = linspace(0, 2 * pi, 10);
% y = @(x)exp(-x) .* sin(x);
lspcf = LSPolynomialCurveFitting(x, y(x), 10);
sol = lspcf.fit()
lspcf.plt_polynomial
hold on
xi = linspace(min(x), max(x), 100);
plot(xi, y(xi), "r--", "LineWidth", 1.5)
legend("拟合曲线", "拟合点", "真实函数", "Location", "best")
legend("boxoff")
hold off结果如下
sol =
包含以下字段的 struct:
C: [11×11 double]
b: [11×1 double]
coefficient: [11×1 double]
fit_poly: - 37.494282546809607481463899603114*t^10 - 0.00000000010713037439474492698364172857389*t^9 + 102.93089907860144194273743778…
fit_error: [0.0019 -0.0132 0.0326 -0.0254 -0.0230 0.0318 0.0354 -0.0371 -0.0636 0.0606 0.0606 -0.0636 -0.0371 0.0354 0.0318 -0.0230 … ]
mse: 0.0014
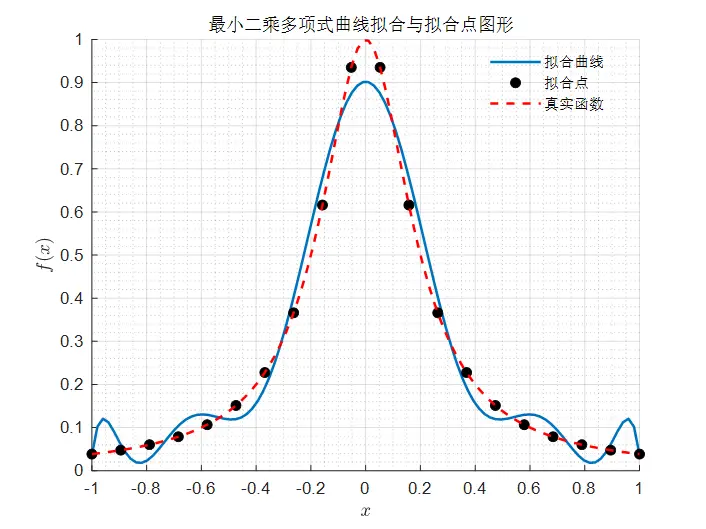
图1 10次多项式曲线拟合
从图1中可以看到,两端点处存在些许振荡现象,盲目提高多项式拟合的阶次,比如20阶,并不会使得拟合的曲线更逼近真实曲线,而是在拟合点处的误差越来越小,mse减少到3.8993e-08,而预测误差反而会增加,出现机器学习中的过拟合现象。如图2所示
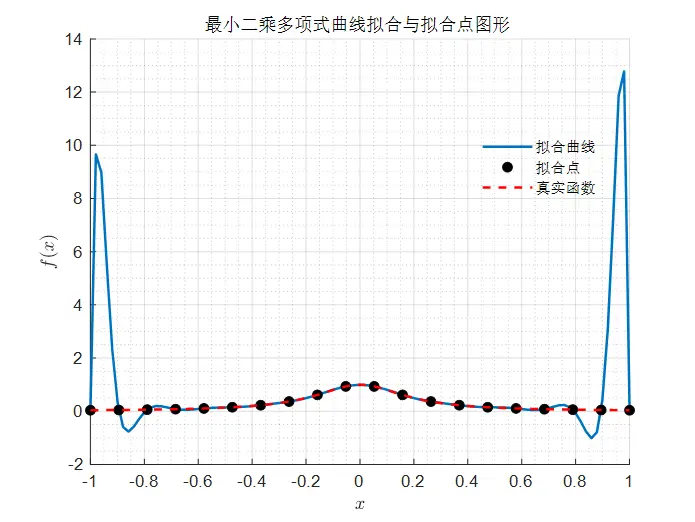
图2 20次多项式曲线拟合
解决这一问题的一个思路是,增加所拟合的数据量,如图3所示,为50个数据量,20次多项式曲线拟合的结果。
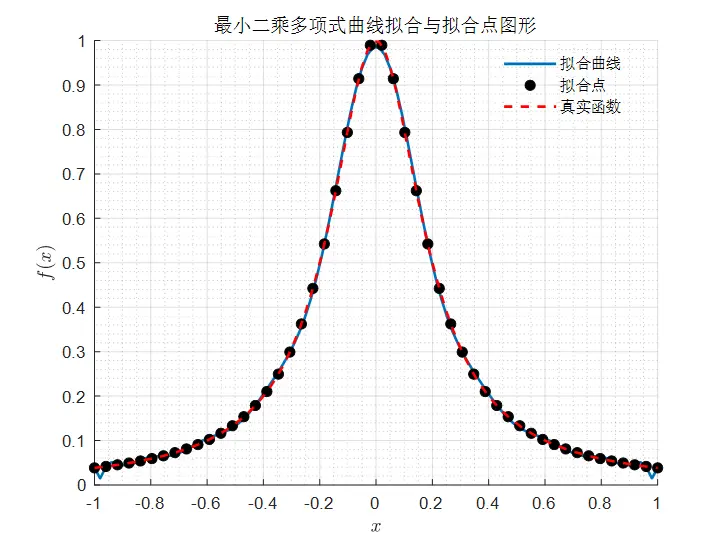
图3 50个数据点的20次拟合曲线
实际应用中,所给定的数据未必知道背后的真实模型,一旦知道背后的真实模型,也就没有拟合的必要了。且采样数据存在一定的误差,故此例模拟。
该示例代码也可进行非线性曲线拟合,但需要进行转换。
例 3:在区间内等分15个数值节点,按照
生成离散数据点,试拟合数学模型
,即确定系数
和
。
x = linspace(-1, 3, 15);
y = 3 * exp(0.5 * x) + randn(1, 15) / 10;
ln_y = log(y); % 线性转换
lspcf = LSPolynomialCurveFitting(x, ln_y, 1);
sol = lspcf.fit()
lspcf.plt_polynomial
a = exp(sol.coefficient(1));
b = sol.coefficient(2);
fprintf("系数分别为:a = %.15f, b = %.15f\n", a, b)
f_true = @(x)3 * exp(0.5 * x); % 真是函数
fh = @(x)a * exp(b * x); % 拟合函数
xi = linspace(min(x), max(x), 100);
plot(xi, fh(xi), "-", "LineWidth", 1.5)
hold on
plot(x, y, "o", "MarkerFaceColor","k", "MarkerEdgeColor", "k")
plot(xi, f_true(xi), "r--", "LineWidth", 1.5)
grid on; grid minor; box off; hold off
legend("拟合曲线", "拟合点", "真实函数", "Location", "best")
legend("boxoff")
xlabel("$x$", "Interpreter","latex")
ylabel("$f(x)$", Interpreter="latex")
title("最小二乘非线性曲线拟合与拟合点图形")结果如下,test_LSPolynomialCurveFitting2为本人定义的脚本文件名称。
>> test_LSPolynomialCurveFitting2
sol =
包含以下字段的 struct:
C: [2×2 double]
b: [2×1 double]
coefficient: [2×1 double]
fit_poly: 0.50457847919108400613907861043117*t + 1.0909972890461916428250788158039
fit_error: [-0.0378 0.0156 -0.0132 0.0191 -0.0118 0.0187 0.0214 0.0371 -0.0017 -0.0326 -0.0120 0.0132 -0.0142 0.0034 -0.0052]
mse: 4.1078e-04
系数分别为:a = 2.977241763092665, b = 0.504578479191084由于数据存在一定的噪声,故拟合的系数与真实系数存在些许误差。
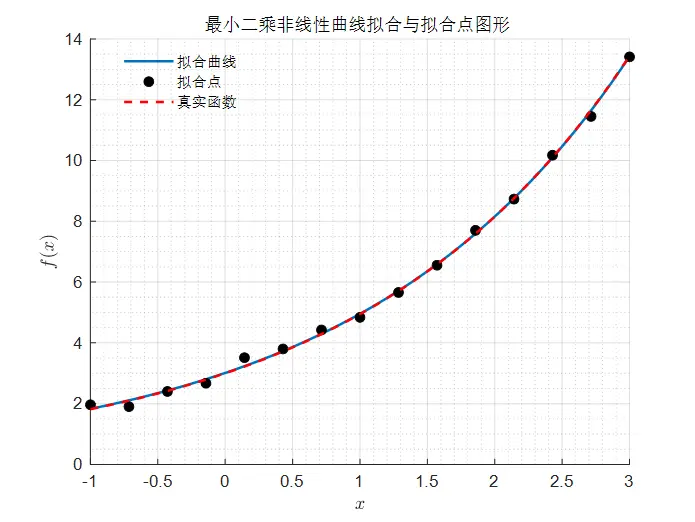
图4 非线性曲线拟合