Matlab基础语法4

matlab提供了一些处理多项式的专用函数，用户可以很方便地进行多项式的建立、多项式求值、乘法和除法运算，以及求多项式的倒数和微分、多项式的根、多项式的展开和拟合等。

一、多项式的建立

对于多项式，用多项式的系数按照降幂次序存放在向量中，顺序必须是从高到低进行排列。例如，多项式可以用系数向量来表示。多项式就转换为多项式系数向量问题，在多项式中缺少的幂次要用0来补齐。

通过ploy2sym()将向量转换为多项式

如果通过多项式的根建立，可以使用ploy()来创建多项式

二、多项式的求值与求根

1.多项式求值

ployval()：以数组或矩阵中的元素为计算单位

y=polyval(p,x)计算多项式系数向量p在x处的函数值

ployvalm()：以矩阵为计算单位

2. 多项式求根

roots()：

三、多项式的乘法和除法

conv()对多项式进行乘法运算，其调用格式为c=conv(a,b)，其中a和b为多项式的系数向量，该函数实现向量a和b的卷积，在代数上相当于多项式a乘以多项式b，其中c为相乘所产生的多项式的系数向量。

四、多项式的求导和积分

polyder(p):向量p为系数的多项式求导

polyder(a,b):对以向量a和b为系数的多项式的乘积进行求导

[q,d]=ployder(b,a):返回以b为系数的多项式除以以a为系数的多项式的商的导数，并以q/d格式表示

ployint(p,k)：返回以向量p为系数的多项式的积分，积分常数为k

polyint(p)：积分常数为0

五、多项式展开

有理多项式用他们的分子多项式和分母多项式进行表示，函数residue()可以将多项式之比用部分分时展开，也可以将一个部分分式用多项式之比进行表示。

[r,p,k]=residue(b,a):求多项式之比b/a的分式展开，函数的返回值r是余数，p是部分分式的极点，k是常数项。

六、多项式的拟合

函数polyfit()采用最小二乘法对给定的数据进行多项式拟合，得到该多项式的系数。该函数的调用方式为：p=polyfit(x,y,n)，采用n次多项式来拟合数据x和y，得到以p为系数的多项式。该函数使得p(x)与y最小均方误差最小。

七、插值

1.一维多项式插值：interp1()

2.一维快速傅里叶插值：interpft()

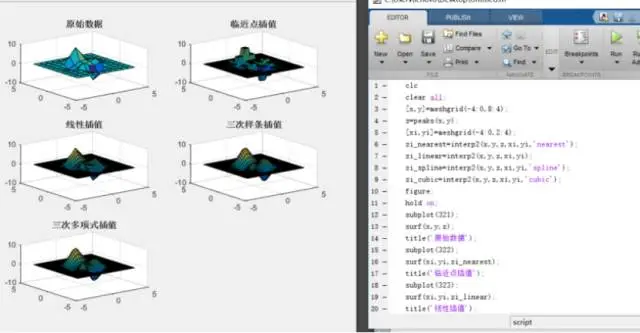
3.二维插值：图像处理，数据的可视化interp2(x,y,z,xi,yi):通过初始数据x、y和z产生插值函数y=f(x,y)，返回zi是（xi,yi）在函数f(x,y)上的值

或者使用interp2(x,y,z,xi,yi,method):其中method采用的插值方法可选择为“nearest”，“linear”，“spline”和“cubic”，其中线性插值为默认的插值方法。

八、函数的极限

使用limit()计算函数的极限

y=limit(f):当x趋近于0时，对该函数求极限

y=limit(f,x,a)：当x趋近于常熟a是，对函数f求极限

y=limit(f,x,a,’left’):左极限

y=limit(f,x,a,’right’):右极限

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删