MATLAB
————Matrix laboratory
一般操作:
1.操作界面:主窗口,命令窗口,工作空间窗口,当前目录窗口和搜索路径
2.帮助系统: help命令 lookfor命令
help 函数名
help(‘函数名’)
lookfor 函数名 %lookfor命令更加宽松,检索所有m文件返回包含函数名的全部函数
3.注释:%这是一条注释
4.语句后加;不显示结果
5.clc 清空命令行窗口,clf 清除figure上图像
数值类型:整型,浮点型 字符类型
注意:
1.MATLAB的处理对象是矩阵(可以理解为MATLAB系统实现了矩阵这种特殊数据结构,数据以矩阵形式进行存储操作——数据类型是针对矩阵元素)
2.向量和标量可以看作特殊的矩阵
3.没有布尔类型,但是以非0表示真,0表示假
4.一般情况下矩阵的元素是相同的数据类型,但是也有将不同类型的数据构成矩阵的元素的数据结构——特殊的矩阵——结构,单元矩阵
变量:对象的引用,代表若干内存单元,通过变量名来对变量所引用的对象进行访问
1.命名规则: 字母开头,后接字母、下划线或数字
2.预定义变量
系统本身定义的变量,尽量避免对这些变量赋值,会覆盖原来的含义
ans——计算结果默认赋值变量
eps——机器零阈值
pi——π的近似值
i,j——虚数单位
inf,Inf——无穷大
NaN,nan——非数,如0/0,inf/inf
nargin——函数输入参数个数
nargout——函数输出参数个数
3.变量管理
命令行窗口:
内存变量的显示——who, whos(内容更详细)
内存变量的删除——clear, clear 变量名列表 (多个之间用空格隔开)
工作区窗口:编辑或删除
4.内存变量文件
利用MAT文件可以把当前MATLAB工作空间中的变量保留下来
MAT文件是一种二进制格式文件,文件后缀.mat
变量写入文件与导入matlab通过save和load命令:
save 文件名 [变量名列表]
load 文件名 [变量名列表]
当然可以通过主窗口的界面操作进行保存与导入
注:
1.文件名不需要加引号,不需要带文件后缀.mat,可以带路径
2.变量名列表中变量的个数不限,省略则默认写入/导入所有的变量,多个变量名之间用空格隔开
3.load 是覆盖的写入,要想追加,则加上 空格-append
5.数据的输出格式
数据的表示常用:日常记数法和科学记数法 1e2——10^2, e,E表示10为底的指数
数据的输出格式靠format命令来设置
format 格式符
格式符常见:short(默认的) long rat(近似有理数)
注意:
1.short输出带4位小数,不超过7位有效数字,
大于1000带小数(非0)的实数用5位有效数字的科学记数法
2.如果输出的矩阵(标量是特殊的矩阵)的每个元素数值是整的,则以不带小数的纯整数格式显示
有一个不是,都是默认小数形式输出
3.每个数据元素的表示和存储都是双精度,format只影响数据的显示,不影响数据的存储
介于MATLAB处理的基本对象是矩阵数据结构,即以矩阵为基本处理单元,我们重点讨论矩阵。
1.矩阵的建立
直接输入——[]括起来,同一行元素用空格或逗号隔开,不同行用分号隔开,注意合法性
M文件建立——M文件编辑,命令行输入文件名创建变量
2.冒号表达式
产生向量[ … ](特殊的矩阵)
start:step:end
省略步长,默认=1
linspace(start,end,number)与 start:(end-start)/number:end等价
3.矩阵的拆分
a、 下标(subscript)和序号(index)——按列编号
下标和序号之间可以转换——sub2ind,ind2sub
index=sub2ind(size(A),i,j)
[i,j]=ind2sub(size(A),index)
参数可以是矩阵,两个矩阵代表下标方式,一个矩阵代表序号方式
注意: 当索引大于原来矩阵的行数/列数/总编号,MATLAB会自动拓展矩阵,并且拓展后未赋值的矩阵元素置为0
A=[1,2,3;4,5,6;7,8,9];
>> A([2,4])
ans =
4 2
>> A([1;2])
ans =
1
4
>> A([1,3],[1,3])
ans =
1 3
7 9
>> A([1;3],[1;3])
ans =
1 3
7 9
b、冒号表达式
A(:,j)——第j列
A(i:i+m,:)——第i到i+m行
A(i:i+m,j:j+n)——i到i+m行j到j+n列交叉的部分
A(:)将矩阵的元素按列叠成一个列向量
end运算符可以表示某一维的末尾
c、利用空矩阵删除矩阵元素
单引号或双引号括起来的字符序列,MATLAB将字符串当作一个行向量,每个元素对应一个字符
相关函数:
1.eval(s) %s为字符串,表示将字符串的内容当作MATLAB语句来执行
>> A
A =
1 2 3
4 5 6
7 8 9
>> y='sin(A).*2+cos(A)'
y =
'sin(A).*2+cos(A)'
>> eval(y)
ans =
2.2232 1.4024 -0.7078
-2.1672 -1.6342 0.4013
2.0679 1.8332 -0.0869
注意: MATLAB中字符串的拼接不能使用+,但是由于MATLAB按ASCII码存储字符串,
所以字符串可以进行算术运算
>> 'adkj'+2
ans =
99 102 109 108
>> 'wy'*2
ans =
238 242
>> 'wy'^2
错误使用 ^ (line 51)
用于对矩阵求幂的维度不正确。请检查并确保矩阵为方阵并且幂为标量。要执行按元素矩阵求幂,请使用 '.^'。
>> ['wy';'wy']^2
ans =
28560 29040
28560 29040
>> 'wy'.^2
ans =
14161 14641
2.strcat用于字符串的拼接,
strcat(s1,s2)
3.字符串类型与其他类型的转换函数
int2str
num2str
mat2str
setstr——将ASCII码值转换为对应字符
str2num
>> a=str2num('ad')
a =
[]
>> str2num('a')
ans =
[]
>> help str2num
str2num - 将字符数组转换为数值数组
此 MATLAB 函数 将字符数组或字符串标量转换为数值矩阵。输入可以包含空格、逗号和分号,以指示单独的元素。如果 str2num
不能将输入解析为数值,则返回空矩阵。
X = str2num(chr)
[X,tf] = str2num(chr)
另请参阅 cast, char, hex2num, num2str, sscanf, str2double
str2num 的参考页
名为 str2num 的其他函数
>> num2str(1)
ans =
'1'
>> int2str(20)
ans =
'20'
>> mat2str(A)
ans =
'[1 2 3;4 5 6;7 8 9]'
>> str2num('23')
ans =
23
>> str2num('[1,2]')
ans =
1 2
>> str2mat('2')
ans =
'2'
>> help str2mat
str2mat - (不推荐)基于字符串构建用空白进行填补的字符数组
此 MATLAB 函数 构成字符数组 S,其中包含字符数组 T1, T2, T3, ...
S = str2mat(T1, T2, T3, ...)
4.strcmp - 比较字符串
此 MATLAB 函数 比较 s1 和 s2,如果二者相同,则返回 1 (true),否则返回 0
(false)。如果文本的大小和内容相同,则它们将视为相等。返回结果 tf 的数据类型为 logical。
tf = strcmp(s1,s2)
>> strcmp('c','c')
ans =
logical
1
>> strcmp('a','c')
ans =
logical
0
>> strcmp('c','a')
ans =
logical
0
1.算术运算+、-、*、/、\、%、^
注意: 这些算术运算是在矩阵意义下进行的,单个数据的算术运算只是一个特例
±运算规则:矩阵维数一致,对应元素±,否则出错,但是标量和矩阵可以进行运算,矩阵的每个元素和标量均进行±
乘运算规则:矩阵要可乘的,遵循矩阵乘法规则,矩阵和标量可乘,矩阵的每个元素均和标量相乘
/、\规则: B 除 A : A / B = A ∗ i n v ( B ) , A B = i n v ( A ) ∗ B B除A:A/B=A*inv(B),A\ B=inv(A)*B B除A:A/B=A∗inv(B),A B=inv(A)∗B,注意除数与被除数
标量可同时为除数与被除数,单独为除数,但不能单独为被除数
^规则:A ^x,要求A为方阵(标量为特例),x为标量
点运算:
.* , .\, ./, .^
矩阵的点运算,如果矩阵维数一样,则对应元素进行运算
当有标量时,标量和矩阵的每个元素进行运算
尤其乘方:
A ^x , A . ^B , A. ^x, x . ^A
A,B表示矩阵(标量,向量是特例),x为标量
当A,B不是标量时A,B需至少有一维相同,矩阵则对应元素乘方
向量与矩阵.^时,行向量时矩阵每行均与行向量对应元素乘方,列向量时,矩阵每列均与列向量对应元素乘方
>> A
A =
1 2 3
4 5 6
7 8 9
>> A^2
ans =
30 36 42
66 81 96
102 126 150
>> A.^2
ans =
1 4 9
16 25 36
49 64 81
>> A.^A
ans =
1 4 27
256 3125 46656
823543 16777216 387420489
>> 2.^A
ans =
2 4 8
16 32 64
128 256 512
>> A.^[1,2,3]
ans =
1 4 27
4 25 216
7 64 729
>> A.^[1;2;3]
ans =
1 2 3
16 25 36
343 512 729
>> A.^[1,2]
错误使用 .^
矩阵维度必须一致。
>> [1,2,3].^A
ans =
1 4 27
1 32 729
1 256 19683
>> [1;2;3].^A
ans =
1 1 1
16 32 64
2187 6561 19683
2.关系运算
<,>,=,~=,≤,≥
规则:
比较量为标量时,直接比较大小,成立返回1,否则返回0;
为同维度矩阵时,对应元素进行关系运算;
标量与矩阵则标量与矩阵的每个元素进行关系运算
3.逻辑运算
&,|,~
(&&,||只用于标量)
运算规则同关系元素类似
优先级(大体上):~单目运算符>算术运算符>关系运算符>逻辑运算符
注意:
1.涉及矩阵的运算且要的是对应元素进行运算时要注意使用点运算,尤其是和函数一起时不要忘记了
2.可以巧妙运用关系运算和逻辑元素对函数值进行分段处理
MATLAB提供的函数自变量规定为矩阵,然而运算法则是将函数逐项作用于矩阵的元素上,因而运算结果是一个与自变量同维的矩阵
sin,cos,tan,sinh,cosh,tanh
asin,acos,atan,asinh,acosh,atanh
sqrt
log——自然对数函数
log10——常用对数函数
log2——以2为底的对数函数
log_M(N)=log(M)/log(N)=log10(M)/log10(N)
exp
pow2
abs
rem,mod(模运算)
fix,round,ceil,floor(取整)
angle,real,imag,conj(复数共轭元素conjugate)
sign(符号函数)
gcd(最大公因子)
lcm(最小公倍数)
xor(异或)
find(返回非零元素的位置,给定两个接受变量得到下标索引,不给定或者给一个得到序号索引)
all 若向量的所有元素非零,则返回1(参数为矩阵的话,以列向量作为一个向量处理,返回结果是针对每列向量的一个横向量,可以指定维数转为行向量)
abs:可以求实数的绝对值,复数的模,字符串的ASCII
fix,round,ceil,floor:fix直接去掉小数部分,round四舍五入,ceil向上取整,floor向下取整
rem,mod区别在涉及负数时不一样
rem(x,y)=x-y.*fix(x./y)
mod=x-y.*floor(x./y)
size(A)——返回矩阵的行数和列数
length(A)——=max(size(A))
ndims(A)——给出A的维数
reshape(A,m,n)——在保持总元素个数不变的情况,对矩阵进行重排
>>help ndims
ndims - 数组维度数目
此 MATLAB 函数 返回数组 A 的维数。维数总是大于等于 2。函数会忽略 size(A,dim) = 1 所针对的尾部单一维度。
N = ndims(A)
1.特殊矩阵
a、通用的特殊矩阵:zeros,ones,eye,rand(产生0~1间均匀分布的随机矩阵),randn(产生均值为0,方差为1的标准正态分布随机矩阵)
以上函数的调用格式相差无几,以zeros为例
zeros(m)——mxm矩阵
zeros(m,n)——mxn矩阵
zeros(size(A))——和矩阵A同大小的矩阵
建立随机矩阵: [a,b]均匀分布的n阶随机矩阵: r a n d ( n ) ∗ ( b − a ) + a rand(n)*(b-a)+a rand(n)∗(b−a)+a 均值为μ,方差为 σ 2 \sigma^2 σ2的n阶正态分布的随机矩阵: μ + σ ∗ r a n d n ( 5 ) μ+\sigma*randn(5) μ+σ∗randn(5) . 例子: 在[20,50]均匀分布的5阶随机矩阵: r a n d ( 5 ) ∗ 30 + 20 rand(5)*30+20 rand(5)∗30+20 均值为0.6方差为0.1的5阶正态分布的随机矩阵: 0.6 + s q r t ( 0.1 ) ∗ r a n d n ( 5 ) 0.6+sqrt(0.1)*randn(5) 0.6+sqrt(0.1)∗randn(5)
b、用于专门学科的特殊矩阵
1)魔方矩阵magic(n) ——n≥3
每行每列及对角线上的元素之和相等
2)范德蒙德矩阵
vander(V)生成以向量V为基础的范德蒙德矩阵
3)希尔比特矩阵
hilb(n)
矩阵元素:h_ij=1/(i+j-1)
希尔伯特矩阵是一个条件数很差的矩阵
4)帕斯卡矩阵pascal(n)
有杨辉三角组成的矩阵——副对角线元素为(x+y)^n的展开式的系数(最高次系数为向量第一分量)
5)多项式的伴随矩阵
compan(p)——p为多项式的系数()
2.矩阵的结构变换
a、对角阵与三角阵
对角阵——除对角元素外的元素均为0,当对角元素相等时称为数量矩阵,特殊地,当对角线元素均为1时为单位矩阵
——提取矩阵对角线元素:
diag(A)提取主对角线元素,产生一个min(m,n)的列向量
diag(A,k)提取第k条对角线元素 ,k=0时为主对角线
——构造对角阵
diag(V)产生以V为主对角线元素的矩阵
diag(V,k)产生以V为第k条对角线的矩阵
三角阵——上三角(upper triangle),下三角(lower triangle)
triu(A) 提取A的上三角元素构成上三角矩阵
triu(A,k) 提取A的第k条及以上的元素构成上三角
tril(A),tril(A,k) 下三角
b、转置,旋转与翻转
1)转置
A’ ——当A为复数矩阵时A’既实现了转置也实现了共轭,A.'只实现转置
transpose(A) - 转置向量或矩阵,此 MATLAB 函数 返回 A 的非共轭转置,
2)旋转
rot90(A,k)将矩阵逆时针旋转90°的k倍,k=1时可省略k
3)翻转
左右——fliplr(A)
上下——flipud(A)
c、矩阵正交化
将A的列向量组正交化存入Q:Q=orth(A),则Q’Q=I
d、LU分解
[L,U]=lu(A) %L为下三角阵或其变换形式,U为上三角阵,LU=A [L,U,P]=lu(A) %LU=PA
3.矩阵求值
1)矩阵求逆
A^(-1)——inv(A)
当A不是方阵或者A非满秩时,A不存在逆,但是若能找到与A的转置同型的矩阵B,满足ABA=A, BAB=B,则称B为A的伪逆,也称广义逆矩阵,求伪逆pinv(A)
注意:存在逆时,矩阵的逆与伪逆一般不相等
求逆的方式解线性方程组
Ax=b
x=A\b=inv(A)*b
2)行列式
方阵A的行列式|A|——det(A)
行列式|A|等于矩阵A的特征值之积
3)秩(奇异值)——rank(A)
4)迹—— trace(A)=矩阵的对角元素之和=矩阵的特征值之和(特征方程得)
5)特征值与特征向量eigenvalue ——eig(A)
eig(A),e=eig(A)——得到A的特征值构成的列向量 [P,E]=eig(A)——A的特征向量构成P的列向量,特征值构成对角阵E [P,E]=eig(A,‘nobalance’)——上一个为先对A进行相似变换,这个没有进行相似变换直接求特征值与特征向量
>> A
A =
1 2 3
4 5 6
7 8 9
>> trace(A)
ans =
15
>> eig(A)
ans =
16.1168
-1.1168
-0.0000
>> sum(eig(A))
ans =
15.0000
6)向量和矩阵范数——用来度量向量在某种意义下的长度
a、向量的范数
2-范数——每个分量的平方和开方
1-范数——每个分量的绝对值之和
∞-范数——分量的绝对值取最大值
n=norm(A)——2-范数,欧几里得范数 n=norm(A,inf)——∞范数 n=norm(A,-inf)——求向量元素的绝对值最小值 n=norm(A,1)——1范数,向量元素的绝对值之和 n=norm(A,p)——p范数,norm(A,2)=norm(A)
x=[1,2,6,3,2];
>> n1=norm(x,1)
n1 =
14
>> n2=norm(x)
n2 =
7.3485
>> ninf=norm(x,inf)
ninf =
6
b、矩阵的范数
||A||=max ||Av||,||v||=1 这样定义的范数称为从属于向量的范数
||A||_1= 每列元素的绝对值之和中取最大值
||A||_∞=每行元素的绝对值之和中取最大值
||A||_2=sqrt(λ),λ为A’A的最大特征值
||A||_F=矩阵元素的平方和开方
norm(A)=norm(A,2)——2范数 norm(A,inf)——∞范数 norm(A,1)——1范数 norm(A,‘fro’)——F范数
>> A=[1 3 2;6 5 0;7 1 5];
>> n2=norm(A)
n2 =
11.0975
>> n1=norm(A,1)
n1 =
14
>> ninf=norm(A,inf)
ninf =
13
>> nF=norm(A,'fro')
nF =
12.2474
7)矩阵的条件数
cond_p(A)=||A||_p·||A^(-1)||_p
条件数总是大于1的,越接近1则矩阵的性能越好,反之越差
性能Ax=b,系数矩阵A的个别元素的微小扰动会引起解的很大变化——A为病态矩阵,不会引起——良性矩阵.良性与病态是相对的,条件数就是用来刻画矩阵这种性能
cond(A)——求cond_2(A) cond(A,p)——求cond_p(A)
1.M文件
————由MATLAB命令组成
根据调用方式的不同分为两类:命令文件(脚本文件);函数文件,拓展名均为.m,但是区别在于
1)命令文件没有输入参数也没有输出参数,而函数文件可以带输入和输出参数;
2)命令文件对MATLAB工作空间的变量进行操作,执行结束后变量还在,而函数文件中定义的变量是局部变量,执行完毕后这些变量会被清除
3)命令文件输入文件名可以直接运行,但是函数文件不能直接运行,需要使用调用的方式
2.程序控制结构
顺序结构
数据输入 x=input(提示信息)
数据的输出 disp
选择结构
if end if else end if elseif else end
switch 表达式 case 表达式1 语句1(语句组) case 表达式2 语句2 … otherwise 语句n end
注意:
switch语句和C语言的区别较大switch后的表达式为一个字符串或者标量,case后的表达式还可以是单元矩阵,单元矩阵时,switch表达式的值等于单元矩阵某个元素时,就执行该对应case语句。执行完毕与switch后的表达式匹配的case 后的语句,则进入switch语句后面的语句
try 语句组1 catch 语句组2 end %当语句组1中出现问题则转去执行语句组2
循环结构
for i=1:1:10 语句 end while 语句 end
注意:在for循环体里面改变循环变量对最终的结果没有影响,因为在i=1:1:10中会被重新赋值
clear
clc
s=0;
for i=1:100
s=s+i^2;
end
s % 338350
clear
clc
s=0;
for i=1:100
s=s+i^2;
i=i+5;
end
s % 338350
3.函数
[x,y]=f(m,n)
函数调用f(a,b)
注意:
1.函数名应该和文件名一致,否则调用时以文件名为准
2.函数参数的可调性
函数所传入参数的数目是可调的,matlab预定义变量nargin和nargout分别记录调用该参数时的输入实参和输出实参个数,我们可以根据这两个变量来决定函数进行不同的处理
3.全局变量 global 变量名 (不推荐使用)
在科学研究和工程应用中,除了大量的数值计算外,还有对符号对象进行的运算,即直接对抽象的符号对象进行计算,并将得到的结果以标准的符号形式来表示。符号计算可以获得比数值计算更一般的结果。
matlab提供了一种符号数据类型,相应的运算对象称为符号对象。在进行符号运算之前要先建立符号对象,然后才可以进行符号对象的运算。
符号对象的创建
——sym函数与syms命令
%建立符号变量与符号常量
%sym函数
>> x=sym('x') %定义符号变量
x =
x
>> k=sym('8') %定义符号常量
k =
8
>> x+k
ans =
x + 8
>> whos
Name Size Bytes Class Attributes
ans 1x1 8 sym
k 1x1 8 sym
x 1x1 8 sym
%syms命令——sym函数一次只能定义一个符号变量,使用syms命令一次可以定义多个符号变量,格式 syms a b c d...
>> syms x y z
>> whos
Name Size Bytes Class Attributes
x 1x1 8 sym
y 1x1 8 sym
z 1x1 8 sym
含有符号对象的表达式为符号表达式,符号对象的四则运算和数值运算一样。
符号表达式的化简
simplify(s) %s为符号表达式
符号对象的替换
y1=subs(y,x1) %用x1替换y中的默认变量 y1=subs(y,x,x1) %用x1替换y中的变量x x是符号对象,x1可以是符号对象也可以是数值变量或表达式
>> syms x y
>> y=cos(x)
y =
cos(x)
>> syms z
>> y1=subs(y,z)
y1 =
cos(z)
>> y2=subs(y,x,2)
y2 =
cos(2)
>> plot(2,y2,'r*')
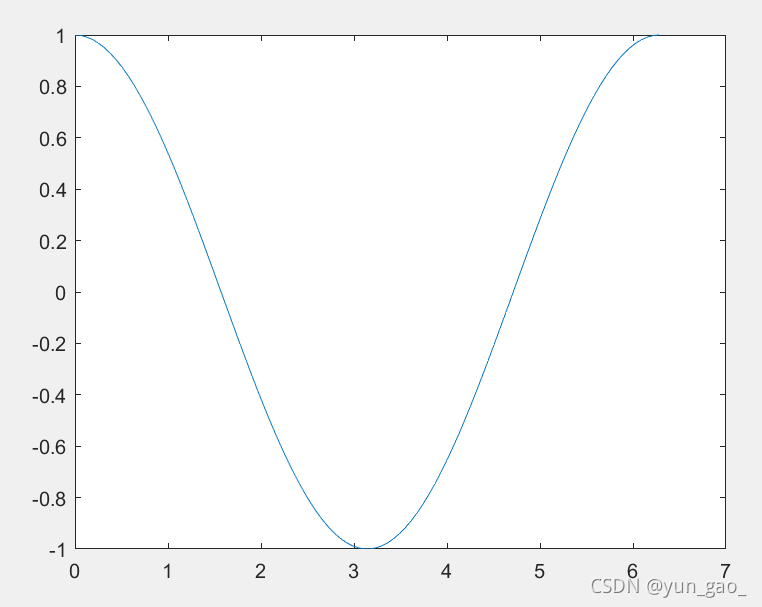
>> t=linspace(0,2*pi,100);
>> e=subs(y,t);
>> plot(t,e)
符号函数
符号对象在微积分中应用很多,常见的符号函数有求极限limit,求导diff,求积分int,求级数symsum,求泰勒级数——taylor,代数方程/方程组solve。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删