使用Matlab实现GA-LSSVM算法仿真

最小二乘支持向量机用网上广为人知的LS-SVMlab工具箱。将下载的压缩包解压（注意不能解压到Matlab的安装目录下），在Matlab主页添加LS-SVM工具箱文件夹，之后就调用m函数就完事了。

       首先照着官方的MatlabLS-SVM工具箱说明书测试了一下分类算法。按照个人的理解，所谓最小二乘支持向量机无非分为两部分：训练部分和测试部分。要求我们调用工具箱之前，要先具备电机运行过程中产生的训练集和测试集。训练集尽量准备尽可能多的样本，以下为例程：

%第一步：生成训练集样本,输入为100*2的矩阵，元素值在-1到1之间，输出为一个莫名其妙的取符号函数

>> X = 2.*rand(100,2)-1;

>> Y = sign(sin(X(:,1))+X(:,2));

%下面是待优化参数，由于现在是LS-SVM的测试环节，这里先赋一个定值

>> gam = 10;

>> sig2 = 0.4;

>> Type = ‘classification’;

%训练得到alpha,b

>> [alpha,b] = trainlssvm({X,Y,type,gam,sig2,'RBF_kernel'});

%训练时原始数据不变

>> [alpha,b] = trainlssvm({X,Y,type,gam,sig2,'RBF_kernel','original'});

%训练时对原始数据进行预处理，可能是归一化处理？

>> [alpha,b] = trainlssvm({X,Y,type,gam,sig2,'RBF_kernel','preprocess'});

%生成测试集

>> Xt = 2.*rand(10,2)-1;

%待测试结果

>> Yorg = sign(sin(Xt(:,1))+Xt(:,2));

%训练结果

>> Ytest = simlssvm({X,Y,type,gam,sig2,'RBF_kernel'},{alpha,b},Xt);

%自定义适应度函数

>> Evaluation = Yorg.'*Ytest

根据仿真结果：

准确率100%，并初步掌握了适应度函数的获取方法，对适应度函数有了一定的概念，为下一步撰写GA遗传算法奠定基础，下一步自然是尝试一下回归算法。

%首先同样建立训练集

>> X = linspace(-1,1,50)';

>> Y = (15*(X.^2-1).^2.*X.^4).*exp(-X)+normrnd(0,0.1,length(X),1);

>> type = 'function estimation';

%下面是工具箱中自带的参数优化语句（采用的是交叉检验法）

>> [gam,sig2] = tunelssvm({X,Y,type,[],[],'RBF_kernel'},'simplex','leaveoneoutlssvm',{'mse'});

%训练得到alpha,b

>> [alpha,b] = trainlssvm({X,Y,type,gam,sig2,'RBF_kernel'});

%得到拟合曲线

>> plotlssvm({X,Y,type,gam,sig2,'RBF_kernel'},{alpha,b});

%生成测试集

>> Xt = rand(10,1).*sign(randn(10,1));

%测试集输出

>> Yorg = (15*(Xt.^2-1).^2.*Xt.^4).*exp(-Xt)+normrnd(0,0.1,length(Xt),1);

%拟合输出

>> Yt = simlssvm({X,Y,type,gam,sig2,'RBF_kernel','preprocess'},{alpha,b},Xt);

%结果

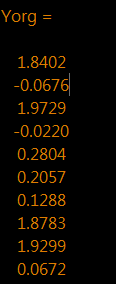
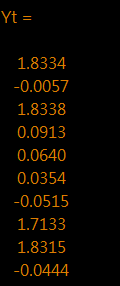
>> adaptability = (Yt - Yorg).'*(Yt - Yorg);

%适应度待评估值

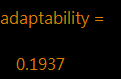
总结：今天确定了回归模型的适应度函数，为GA优化算法奠定了基础，GA拟采用冒泡排序挑选适应度最高的参数。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删