MATLAB实现Kmeans聚类算法仿真研究

1.软件版本

MATLAB2021a

2.本算法理论知识

K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。如果用数据表达式表示，假设簇划分为(C1,C2,...Ck)(C1,C2,...Ck)，则我们的目标是最小化平方误差E：

E=∑i=1k∑x∈Ci||x−μi||22E=∑i=1k∑x∈Ci||x−μi||22

其中μiμi是簇CiCi的均值向量，有时也称为质心，表达式为：

μi=1|Ci|∑x∈Cixμi=1|Ci|∑x∈Cix

3.核心代码

登录后复制

function [U1,U2]=count(u1,u2,x)N1=0;%第一类个数N2=0;%第二类个数for i=1:210d1(i)=dis1(u1,x,i);%x中所有点到u1的欧式距离d2(i)=dis2(u2,x,i);%x中所有点到u2的欧式距离if d1(i)>d2(i)    N1=N1+1;    W1(N1,:)=x(i,:);%划分到W1类中   else    N2=N2+1;    W2(N2,:)=x(i,:);%划分到W2类中     endend%重新计算聚类中心%W1类u=[0 0];for i=1:N1u=u+W1(i,:);endU1=(u/N1);%W2类u=[0 0];for i=1:N2u=u+W2(i,:);endU2=(u/N2);%在图中画出%[~,~,r1,r2,r3,r4]=data3();%plot(r1,r2,'.',r3,r4,'+');%hold on;for i=1:N1 r1(i)=W1(i,1);end;for i=1:N1 r2(i)=W1(i,2);end;for i=1:N2 r3(i)=W2(i,1);end;for i=1:N2 r4(i)=W2(i,2);end;figure(2);plot(r1,r2,'ro',r3,r4,'ms');title('k均值聚类');1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.

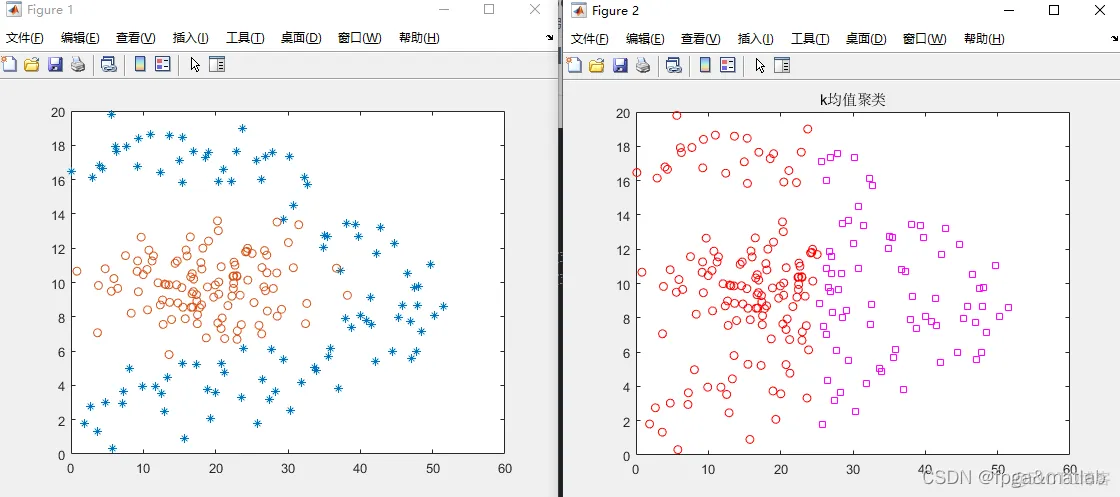
4.操作步骤与仿真结论

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删