蚁群算法模糊聚类MATLAB仿真实现（FCM视角）

1.软件版本

MATLAB2013b

2.本算法理论知识

用FMC 算法实现基于目标函数的模糊聚类又称交替的迭代优化法。迭代优化本质上属于局部搜索的爬山法，很容易陷入局部极值点，因此对初始化很敏感。通常是根据一定的经验准则选取初始参数，这样计算结果与初始参数设置是否恰当密切相关。特别是在数据量较大和高维情况下，设置合理的参数非常困难，只能通过多次实验比较选定。由于初始聚类中心和样本的输入次序对最终的结果有重大影响，往往是用若干不同的初始中心和聚类数目分别聚类，然后选择最满意的聚类作为最终的结果。 通过蚁群算法，我们可以得到最佳的初始聚类中心，然后进行快速的聚类。

3.部分核心代码

登录后复制

clc;clear;close all;warning off;pack;addpath 'func\'%模拟数据MAX_ITER  = 1000;
%最大迭代次数Class_Num = 5;  %样本类别数Nums      = 100 ;%样本数目seek      = 2;  
%数据类别figure;POS       = func_node_gen(Class_Num,Nums,seek);%数据data      = POS(:,1:2);
%首先进行蚁群算法进行优化，获得最佳的初始聚类中心点cluster_center = func_ant_opt(data,Class_Num);
%通过模糊聚类算法进行聚类[U,P]=func_FCM(data,cluster_center,Class_Num,MAX_ITER);
%两个算法的对比figure;load result.matplot(Obj_Fcn(2:end),'b-','LineWidth',2);
hold on;load ..\FCM\result.matplot(Obj_Fcn(2:end),'r-','LineWidth',2);
hold offlegend('蚁群FCM','FCM');axis([0,400,105,125]);grid on;xlabel('迭代次数');
ylabel('聚类误差值'); 1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.
31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.

4.操作步骤与仿真结论

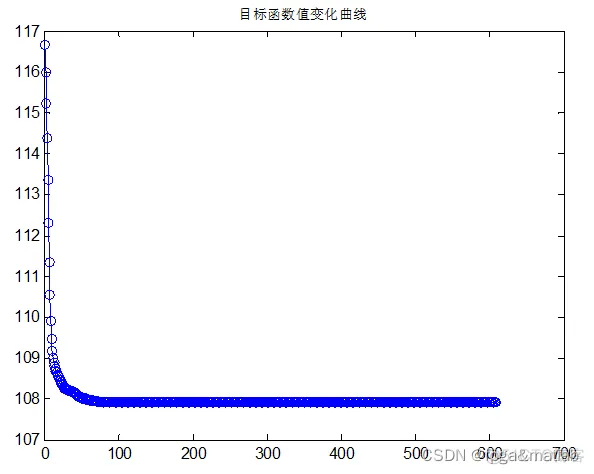
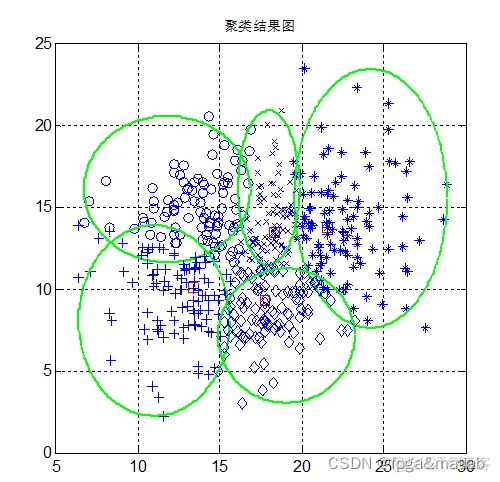
两个算法对比如下所示：

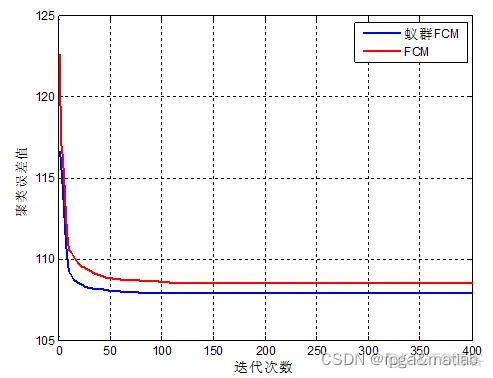
通过对比可知，改进后的算法性能明显提升了。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删