产品
1.算法描述
meanshift算法其实通过名字就可以看到该算法的核心，mean（均值），shift（偏移），简单的说，也就是有一个点 ,它的周围有很多个点 我们计算点 移动到每个点 所需要的偏移量之和，求平均，就得到平均偏移量，（该偏移量的方向是周围点分布密集的方向）该偏移量是包含大小和方向的。然后点 就往平均偏移量方向移动，再以此为新的起点不断迭代直到满足一定条件结束。
登录后复制
中心点就是我们上面所说的 周围的小红点就是 黄色的箭头就是我们求解得到的平均偏移向量。那么图中“大圆圈”是什么东西呢？
我们上面所说的周围的点 周围是个什么概念？总的有个东西来限制一下吧。那个“圆圈”就是我们的限制条件，或者说在图像处理中，
就是我们搜索迭代时的窗口大小。
步骤1、首先设定起始点 ，我们说了，是球，所以有半径 ， 所有在球内的点就是 , 黑色箭头就是我们计算出来的向量 ,
将所有的向量 进行求和计算平均就得到我们的meanshift 向量，也就是图中黄色的向量。
接着，再以meanshift向量的重点为圆心，再做一个高维的球，如下图所示，重复上面的步骤，最终就可以收敛到点的分布中密度最大的地方
算法步骤：
登录后复制
1）在未被标记的数据点中随机选择一个点作为起始中心点center；
2）找出以center为中心半径为radius的区域中出现的所有数据点，认为这些点同属于一个聚类C，同时在该聚类中记录数据点出现的次数加1；
3）以center为中心点，计算从center开始到集合M中每个元素的向量，将这些向量相加，得到向量shift;
4）center=center+shift,即center沿着shift方向移动，移动距离为||shift||；
5）重复步骤2，3，4，直到shift很小，记得此时的center。注意，这个迭代过程中遇到的点都应该归类到簇C；
6）如果收敛时当前簇C的center与其它已经存在的簇C2中心的距离小于阈值，那么把C2与C合并，数据点出现次数也对应合并。
否则把C作为新的聚类；
7）重复1，2，3，4，5直到所有点都被标记为已访问；
8）分类：根据每个类，对每个点的访问频率，取访问频率最大的那个类，作为当前点集的所属类。
登录后复制
对式(33)右边的第二项,我们可以利用Mean Shift算法进行最优化.在Comaniciu等人的文章中,他们只用平均每帧图像只用4.19次Mean
Shift迭代就可以收敛,他们的结果很显示在600MHz的PC机上,他们的程序可以每秒处理30帧352240象素的图像.
下图显示了各帧需要的Mean Shift迭代次数.
2.仿真效果预览
matlab2022a仿真结果如下：
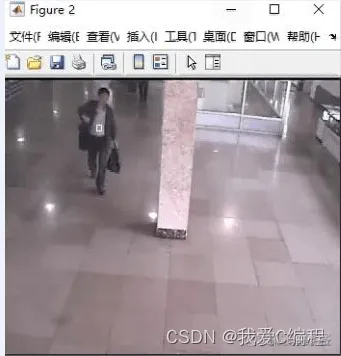
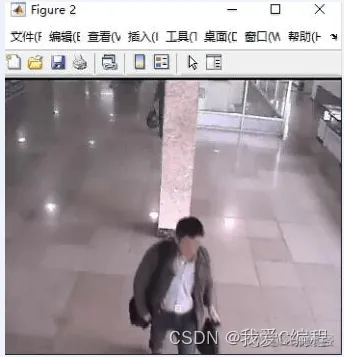
3.MATLAB核心程序
登录后复制
cmin = round(cmin);
cmax = round(cmax);
rmin = round(rmin);
rmax = round(rmax);
wsize(1) = abs(rmax - rmin);
wsize(2) = abs(cmax - cmin);
hsvimage = rgb2hsv(Image1);
% pull out the h
huenorm = hsvimage(:,:,1);
hue = huenorm*255;
hue=uint8(hue);
histogram = zeros(256);
for i=rmin:rmax
for j=cmin:cmax
index = uint8(hue(i,j)+1);
histogram(index) = histogram(index) + 1;
end
end
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
