1 【MATLAB】SG滤波算法

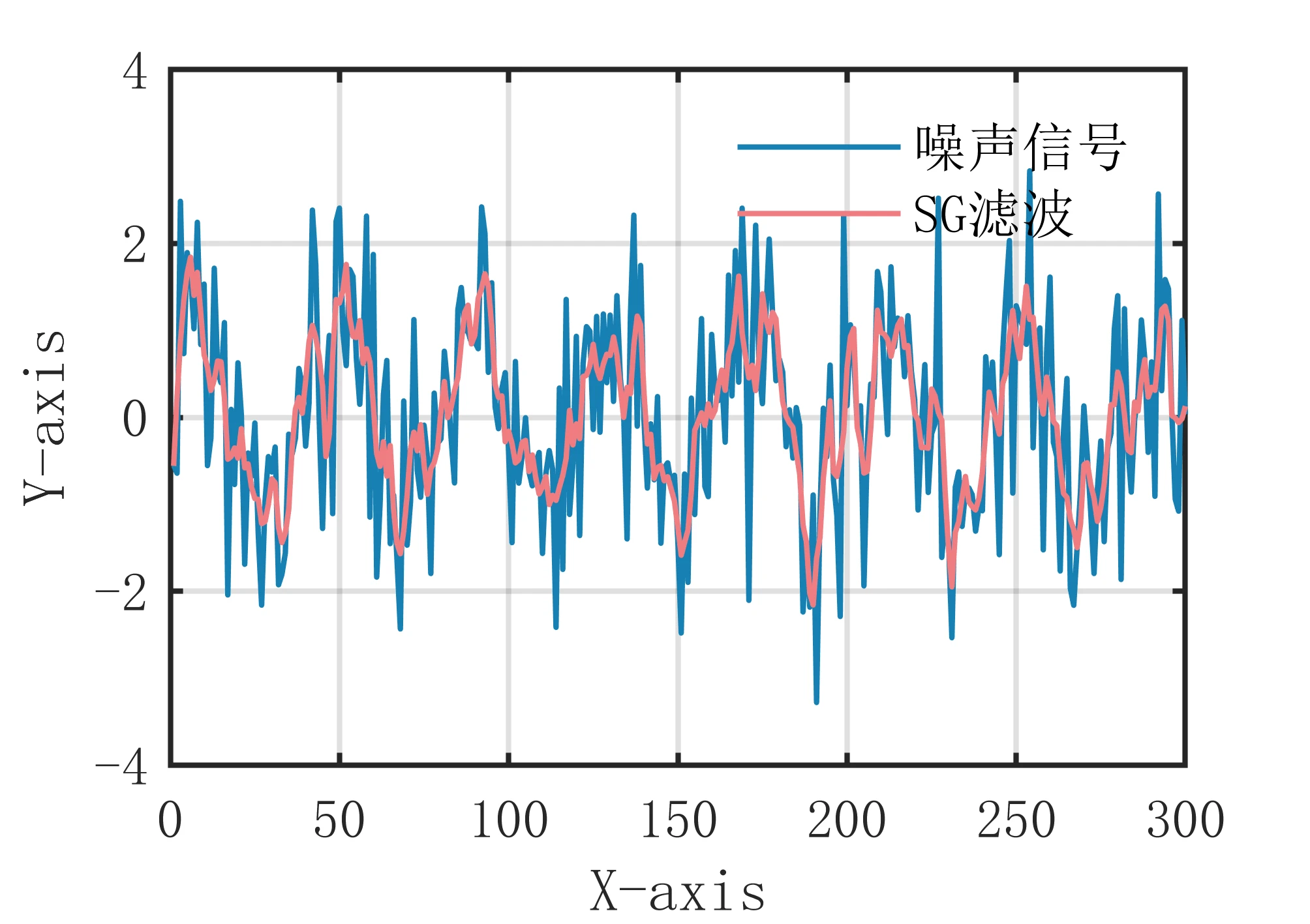
SG 滤波算法（Savitzky - Golay 滤波算法）是一种数字信号处理算法，用于对信号进行平滑处理。该算法利用最小二乘法拟合局部数据段，然后用拟合的函数来估计每个数据点的值，从而实现平滑处理。 SG 滤波算法的优点是可以同时实现平滑和去噪，可以有效滤除高频噪声，对于非线性信号也有较好的适应性。此外，该算法计算速度快，不需要频域转换，适用于实时信号处理。 SG 滤波算法的缺点是需要选择合适的窗口大小和多项式阶数，不同的参数会对滤波效果产生影响。此外，该算法对于信号中存在较大幅值的局部突变或者斜率变化较大的段落，可能会产生较大的误差。在实际应用中，SG 滤波算法可以用于信号平滑、去噪、信号分析等领域。

滤波算法示意图

2【MATLAB】T1小波滤波算法

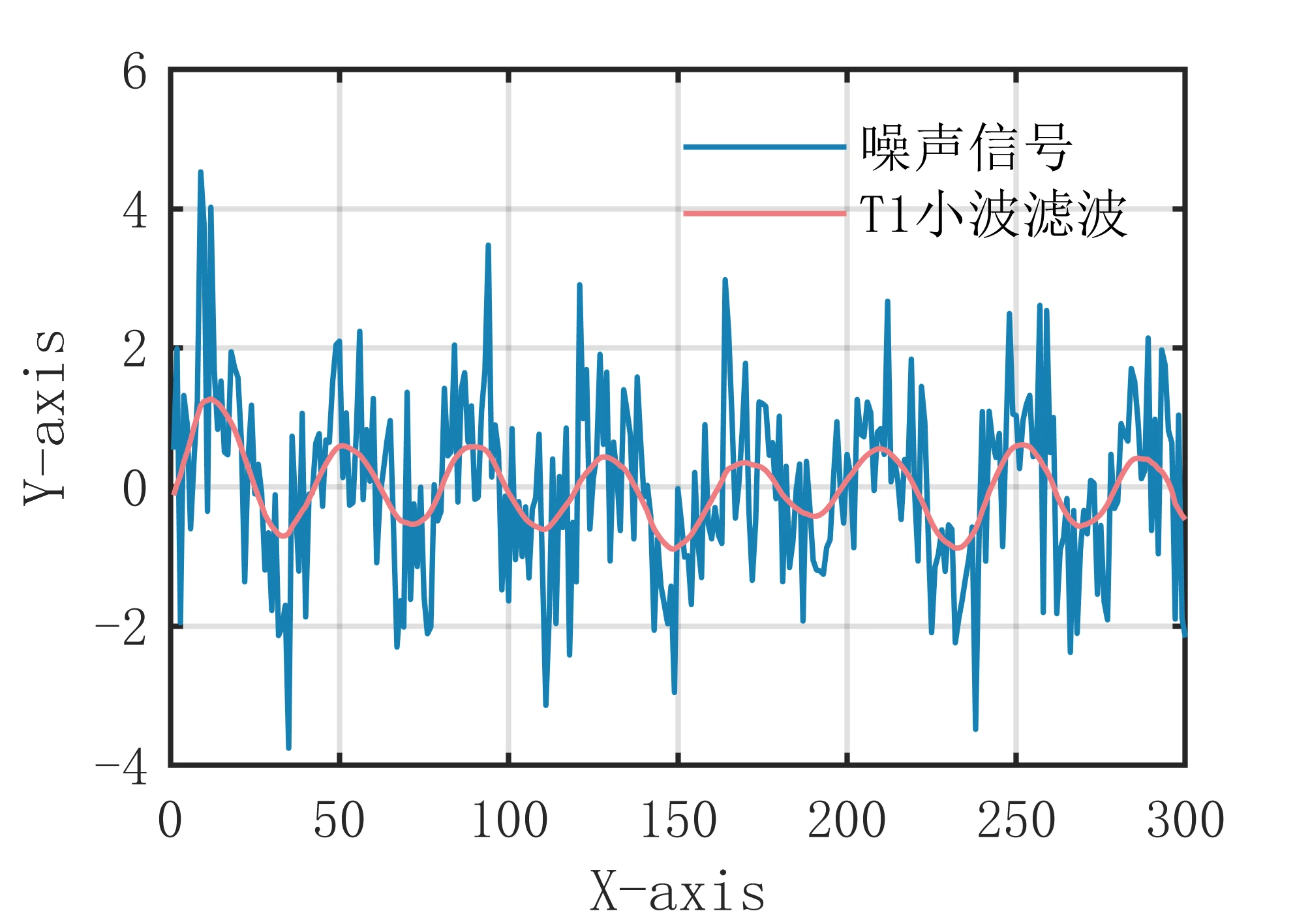
T1小波滤波算法是一种基于小波变换的信号去噪算法。它可以有效地去除信号中的噪声，并保留信号的主要特征。该算法的主要思想是将信号分解为多个不同尺度的小波系数，然后通过对小波系数进行阈值处理来去除噪声。 具体来说，T1小波滤波算法的步骤如下：

1. 将原始信号进行小波分解，得到多个尺度的小波系数。
2. 对每个尺度的小波系数进行阈值处理，将小于某个阈值的系数置为0，保留大于等于阈值的系数。
3. 对处理后的小波系数进行小波重构，得到去噪后的信号。
4. 重复上述步骤，直到满足停止准则。 T1 小波滤波算法的优点是可以保留信号的主要特征，同时去除噪声，能够有效地处理非平稳信号和非线性信号。缺点是需要选择合适的阈值和停止准则，否则可能会影响信号的重构效果。

滤波算法示意图

3【MATLAB】高斯加权移动平均滤波算法

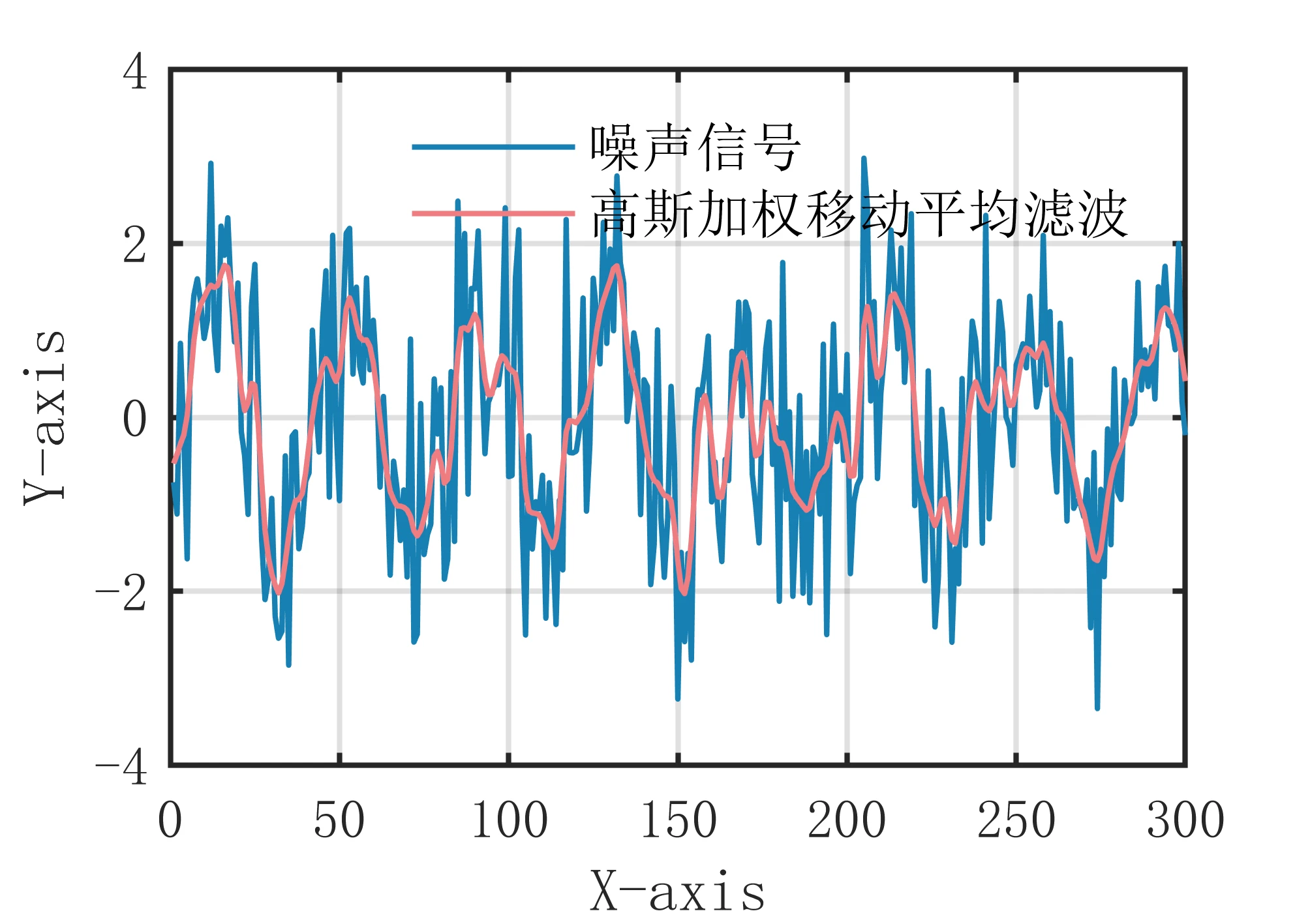
高斯加权移动平均滤波算法是一种基于加权平均的滤波方法，它可以有效地去除高斯噪声，同时保留信号的主要特征。该算法的主要思想是通过对信号进行加权平均来消除噪声，其中权值是根据高斯分布计算得到的，越接近中心点的权值越大，越远离中心点的权值越小。这样可以使得噪声的影响减小，同时保留信号的主要特征。 具体来说，高斯加权移动平均滤波算法的步骤如下：

1. 定义一个滤波窗口，包括当前样本点和其周围的若干个点。
2. 对窗口内的每个点计算其权值，根据高斯分布计算得到，距离当前样本点越远的点权值越小。
3. 对窗口内的每个点的数值进行加权平均，得到当前样本点的滤波结果。
4. 将滤波窗口向前移动一个位置，重复上述步骤，直到所有样本点都被处理完毕。高斯加权移动平均滤波算法的优点是可以有效地去除高斯噪声，同时保留信号的主要特征；缺点是需要选择合适的窗口大小和高斯分布参数，否则可能会影响滤波的效果。

滤波算法示意图

4【MATLAB】滑动平均滤波算法

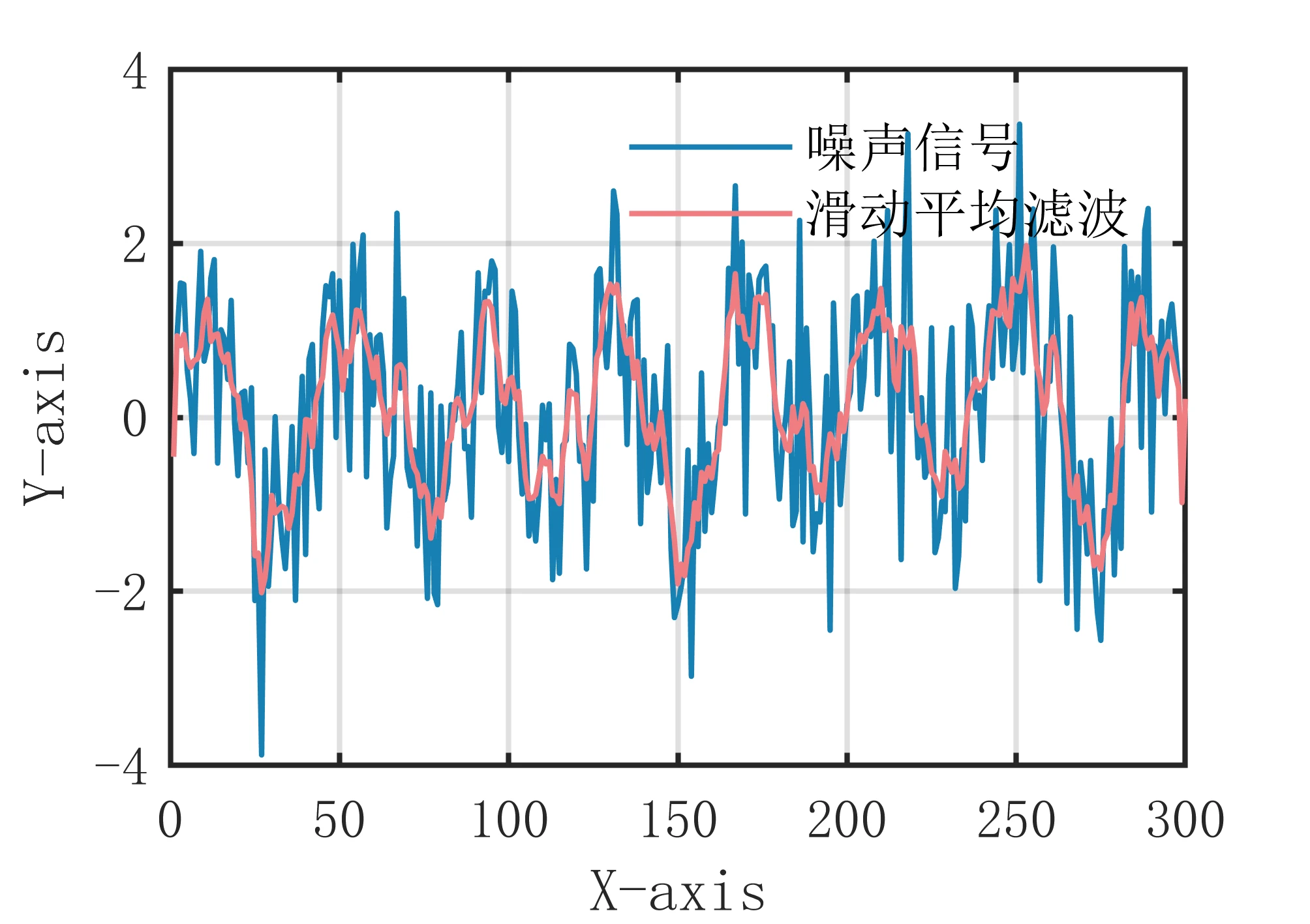
滑动平均滤波算法是一种经典的滤波方法，它通过计算信号的移动平均值来消除噪声。该算法的主要思想是对信号进行滑动窗口处理，窗口内的数据进行平均化，以得到平滑后的信号。这样可以有效地去除周期性噪声和高频噪声，同时保留信号的整体趋势。 具体来说，滑动平均滤波算法的步骤如下：

1. 定义一个滤波窗口，包括当前样本点和其周围的若干个点。
2. 对窗口内的数据进行平均化，得到当前样本点的滤波结果。
3. 将滤波窗口向前移动一个位置，重复上述步骤，直到所有样本点都被处理完毕。滑动平均滤波算法的优点是简单易用，计算效率高，可以有效地去除周期性噪声和高频噪声；缺点是可能会对信号的快速变化造成滞后效应，同时窗口大小的选择也会影响滤波效果。

滤波算法示意图

5【MATLAB】卷积滑动平均滤波算法

卷积滑动平均滤波算法是一种基于卷积操作的滤波方法，它通过对信号进行卷积运算来计算移动平均值，以消除噪声。该算法的主要思想是将滤波窗口的加权系数定义为一个卷积核，对信号进行卷积运算来得到平滑后的信号。这样可以有效地去除周期性噪声和高频噪声，同时保留信号的整体趋势。 具体来说，卷积滑动平均滤波算法的步骤如下：

1. 定义一个滤波窗口，包括当前样本点和其周围的若干个点。
2. 将滤波窗口的加权系数定义为一个卷积核。
3. 对信号和卷积核进行卷积运算，得到当前样本点的滤波结果。
4. 将滤波窗口向前移动一个位置，重复上述步骤，直到所有样本点都被处理完毕。卷积滑动平均滤波算法的优点是可以有效地去除周期性噪声和高频噪声，同时保留信号的整体趋势；缺点是需要选择合适的卷积核大小和加权系数，否则可能会影响滤波的效果。

滤波算法示意图

6【MATLAB】滤波器滤波算法

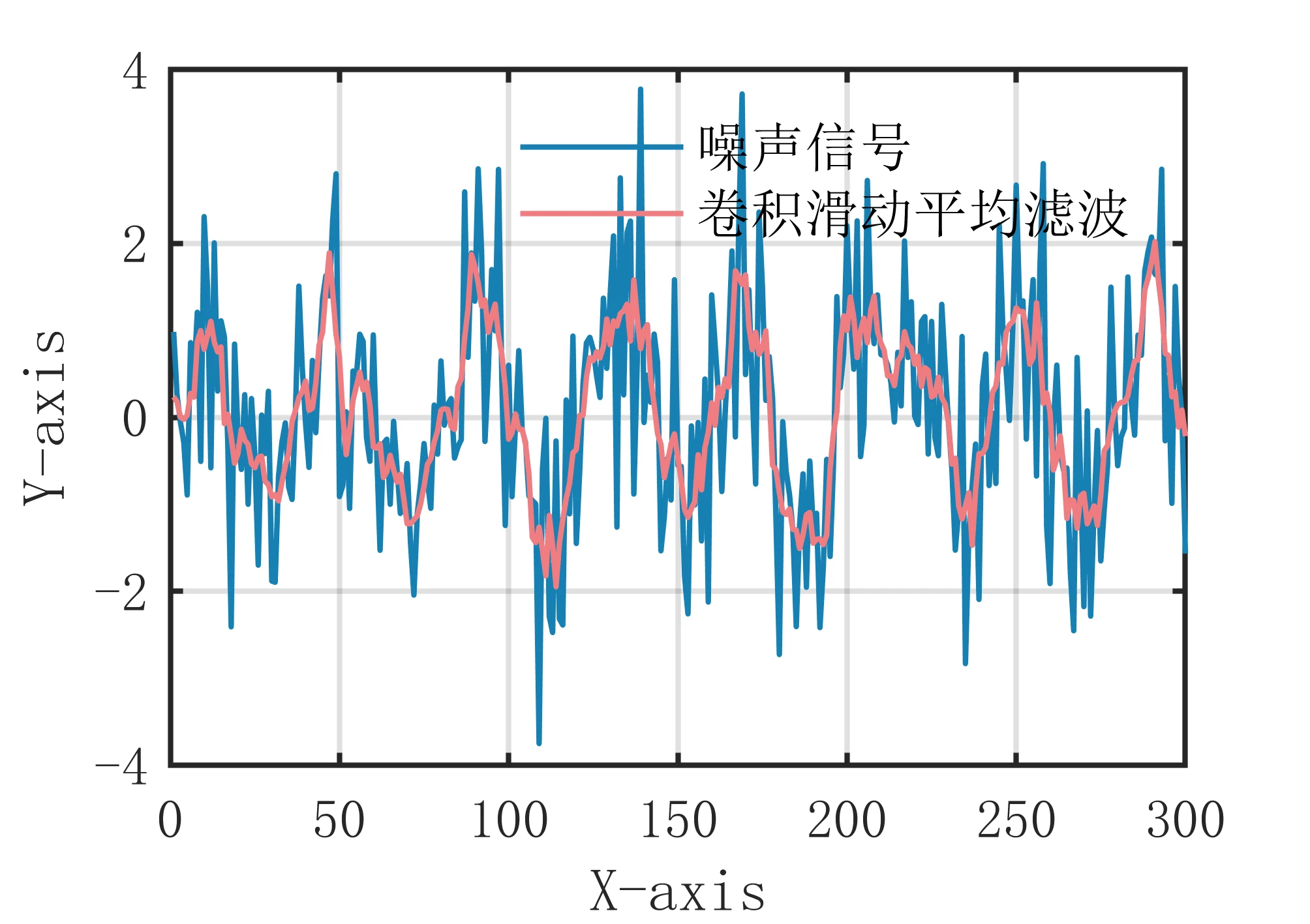
滤波器滤波算法是一种基于数字滤波器的滤波方法，它通过对信号进行滤波器处理来消除噪声。数字滤波器可以分为FIR滤波器和IIR滤波器两种类型，其中FIR滤波器是一种线性相位滤波器，IIR滤波器是一种非线性相位滤波器。这两种滤波器都可以用来对信号进行滤波处理，以消除噪声。 具体来说，滤波器滤波算法的步骤如下：

1. 定义一个数字滤波器，包括滤波器类型、滤波器参数等。
2. 对信号进行滤波器处理，得到滤波后的信号。
3. 对滤波后的信号进行后处理，包括信号放大、平移等操作，以得到最终的滤波结果。滤波器滤波算法的优点是可以根据信号的特点选择不同类型的数字滤波器，以达到最优的滤波效果；缺点是需要对滤波器进行设计和参数调整，复杂度较高，而且滤波器的稳定性和相位响应也需要考虑。

滤波算法示意图

7【MATLAB】小波去噪滤波算法

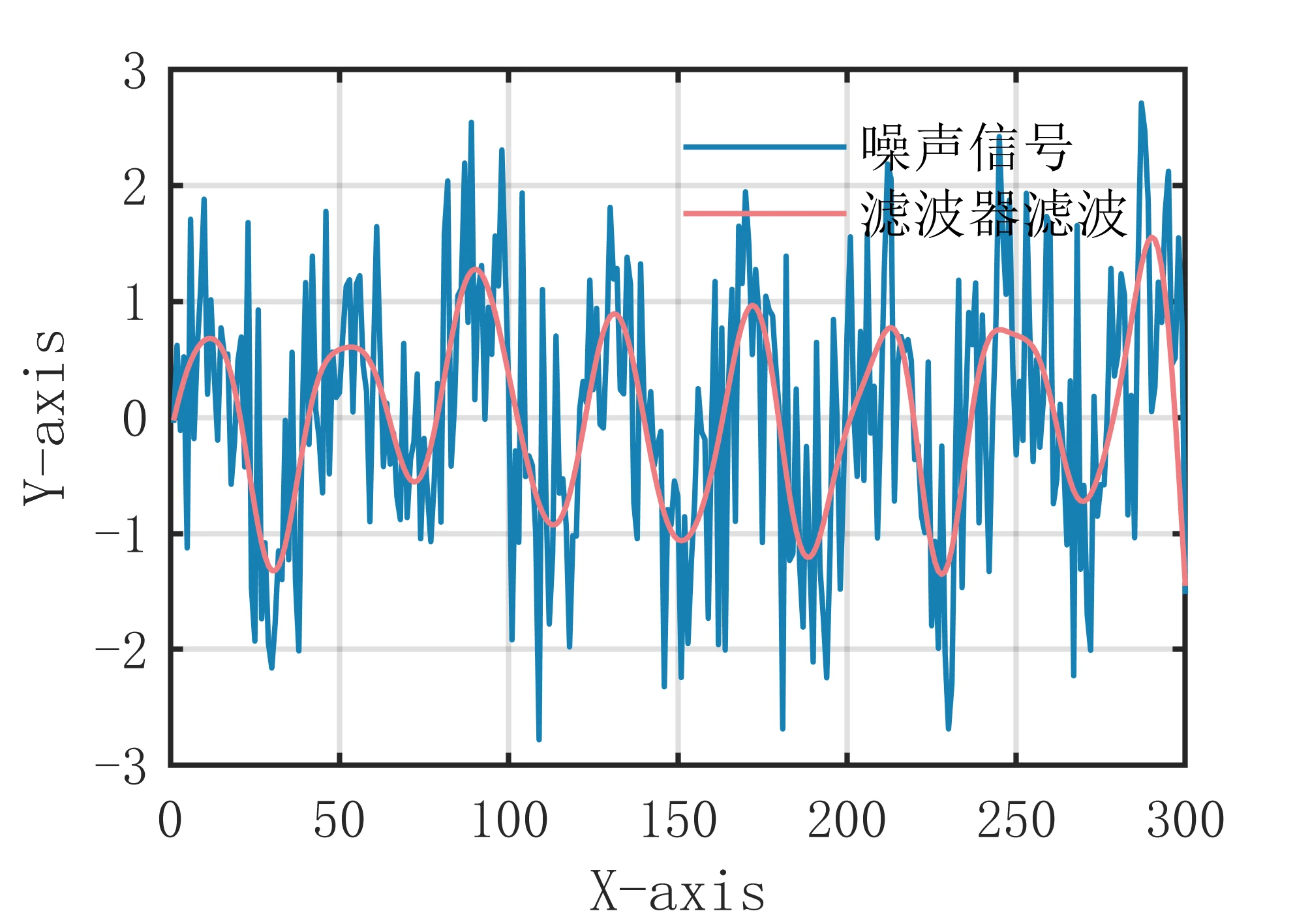
小波去噪滤波算法是一种基于小波变换的滤波方法，它通过对信号进行小波变换来分解信号的频率分量，并根据信号的特点选择合适的阈值处理方法来去除噪声。该算法的主要思想是将信号分解成多个频率分量，根据信号的特点选择合适的阈值处理方法对每个频率分量进行去噪处理，然后将去噪后的频率分量进行合成，得到平滑后的信号。 具体来说，小波去噪滤波算法的步骤如下：

1. 对信号进行小波分解，得到多个频率分量。
2. 对每个频率分量进行阈值处理，去除噪声。
3. 将去噪后的频率分量进行合成，得到平滑后的信号。小波去噪滤波算法的优点是可以有效地去除噪声，同时保留信号的整体趋势；缺点是需要选择合适的小波基和阈值处理方法，否则可能会影响滤波的效果。另外，小波去噪滤波算法对于信号中存在的快速变化的特征可以得到很好的保留，因此在一些需要保留信号快速变化特征的应用场景中，小波去噪滤波算法得到了广泛的应用。

滤波算法示意图

8【MATLAB】一维信号NLM非局部均值滤波算法

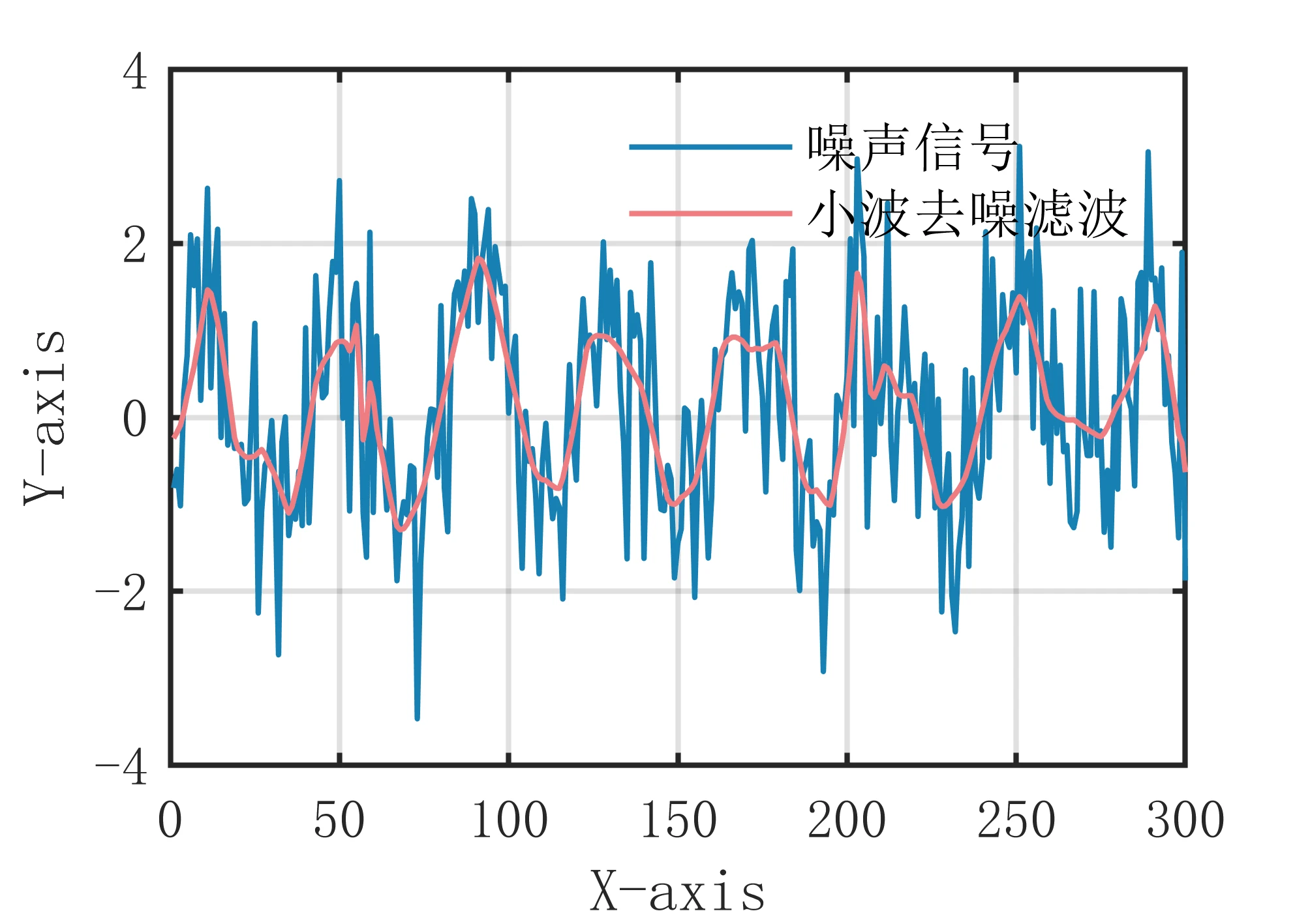
一维信号NLM非局部均值滤波算法是一种基于非局部均值思想的滤波方法，它通过对信号进行分块，计算每个块与其他块之间的相似度，以非局部均值的方式去除噪声。该算法的主要思想是在一定范围内寻找与当前块相似的块，以这些块的非局部均值作为当前块的估计值，以达到去除噪声的效果。 具体来说，一维信号NLM非局部均值滤波算法的步骤如下：

1. 将信号分成多个块，每个块的大小为w。
2. 对每个块，计算它与其他块之间的相似度，以此为依据选择与当前块相似的块。
3. 对选出的块，计算它们的非局部均值。
4. 将这些非局部均值作为当前块的估计值，以去除噪声。一维信号 NLM 非局部均值滤波算法的优点是可以在一定程度上去除噪声，同时保留信号的边缘和细节特征。缺点是需要计算大量的相似度，算法复杂度较高，而且需要选择合适的窗口大小和块大小以达到最优的滤波效果。此外，该算法对于一些信号存在快速变化和较大噪声的情况下，效果可能会有所下降。

滤波算法示意图

9【MATLAB】移动中位数滤波算法

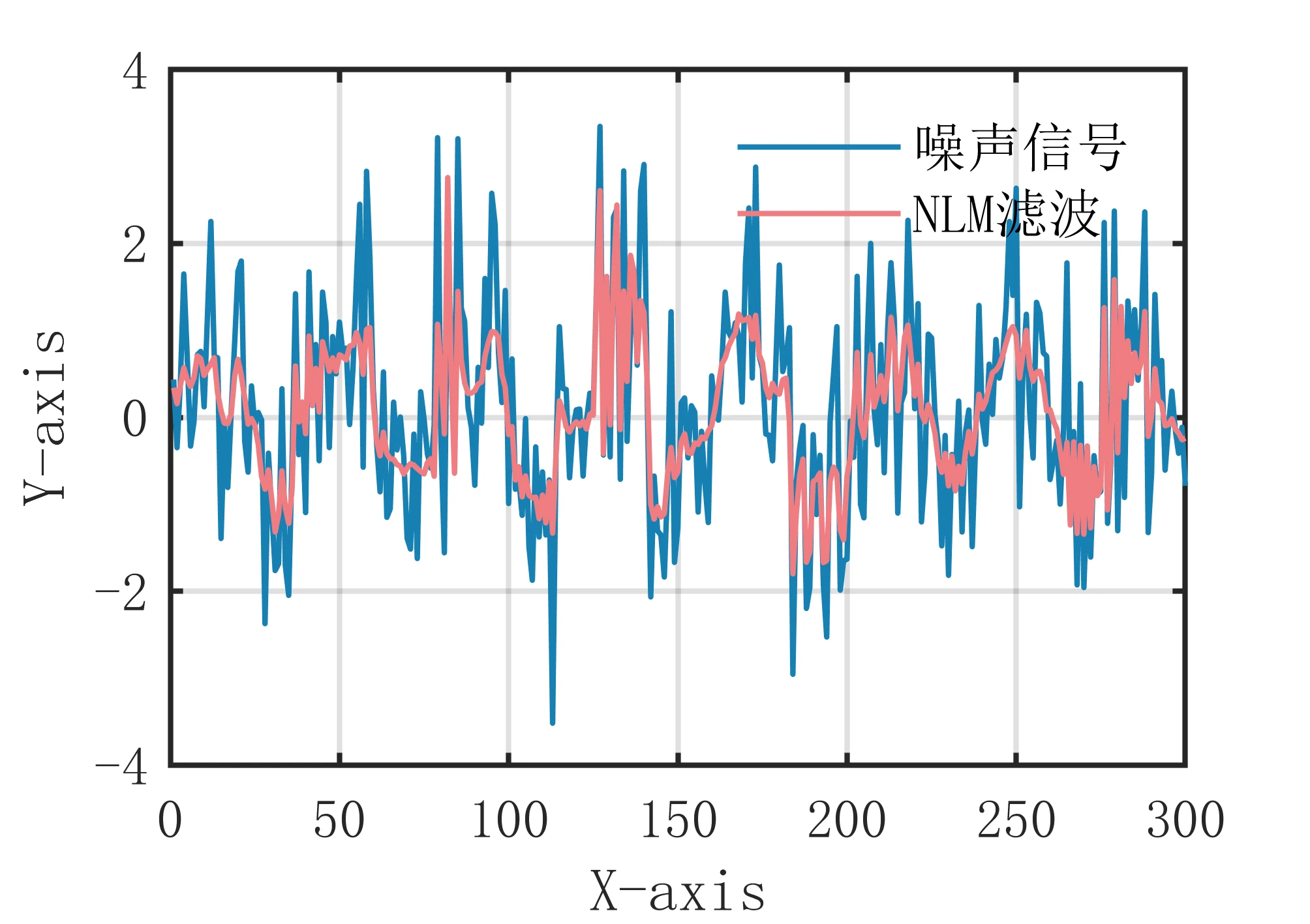
移动中位数滤波算法是一种基于中位数的滤波方法，它通过对信号进行滑动窗口处理，每次取窗口内的中位数作为当前点的估计值，以去除噪声。该算法的主要思想是利用中位数的鲁棒性，对信号中的噪声进行有效的消除。 具体来说，移动中位数滤波算法的步骤如下：

1. 定义一个滑动窗口大小，窗口大小通常为奇数。
2. 将窗口依次向前移动，每次取窗口内的中位数作为当前点的估计值。
3. 重复步骤 2，直到处理完整个信号。移动中位数滤波算法的优点是可以有效地去除噪声，同时保留信号的整体趋势；缺点是对于一些信号存在快速变化的情况下，效果可能会有所下降。此外，该算法也需要选择合适的窗口大小以达到最优的滤波效果。

滤波算法示意图

10【MATLAB】卡尔曼滤波算法

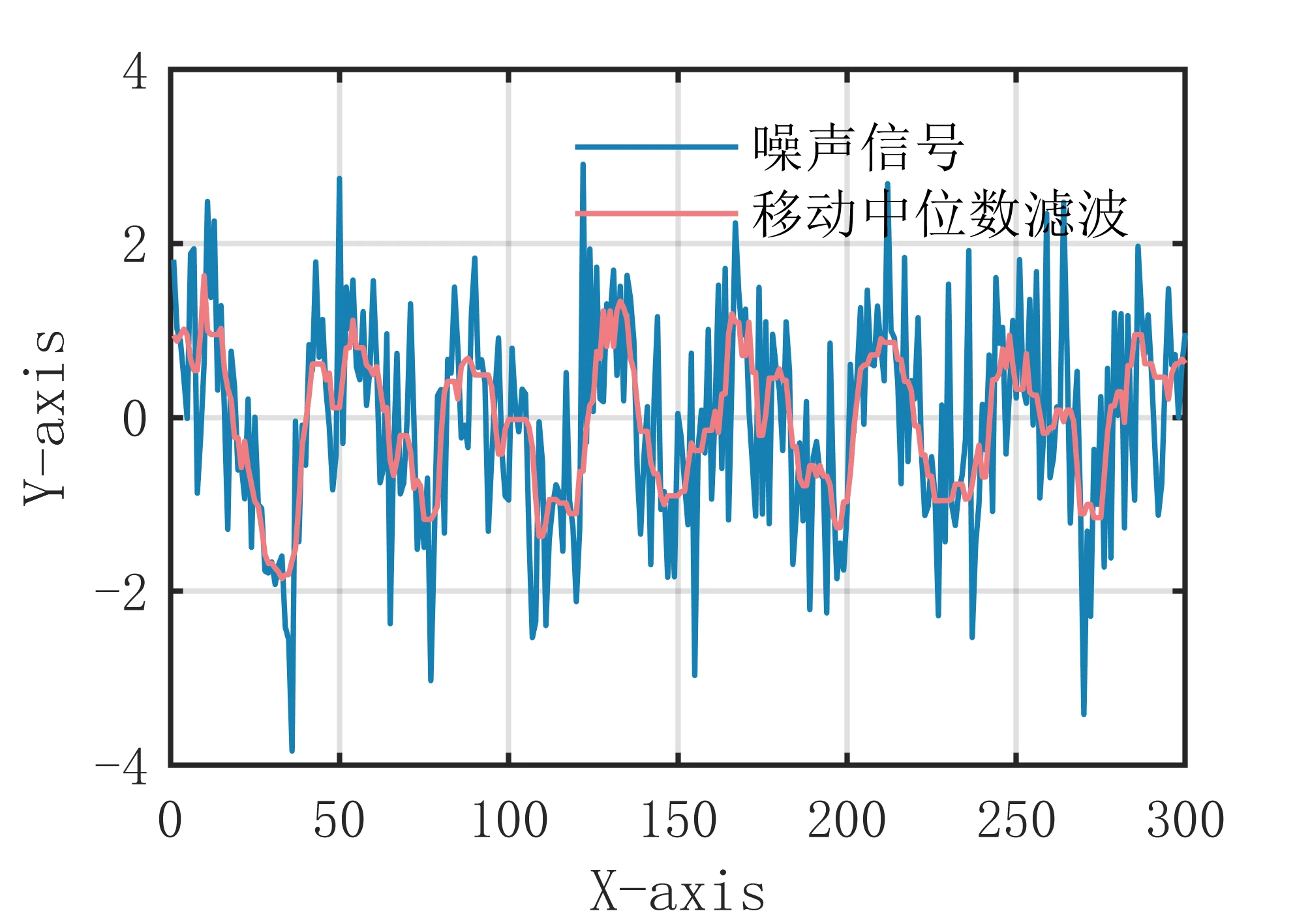
卡尔曼滤波是一种线性最优滤波器，它建立在线性代数和隐马尔可夫模型（hidden Markov model）上。其基本动态系统可以用一个马尔可夫链表示，该马尔可夫链建立在一个被高斯噪声（即正态分布的噪声）干扰的线性算子上的。随着离散时间的每一个增加，这个线性算子就会作用在当前状态上，产生一个新的状态，并也会带入一些噪声，同时系统的一些已知的控制器的控制信息也会被加入。

在实际应用中，目标的动态信息往往存在噪声，卡尔曼滤波利用目标的动态信息，设法去掉噪声的影响，得到一个关于目标位置的好的估计。这个估计可以是对当前目标位置的估计（滤波），也可以是对于将来位置的估计（预测），也可以是对过去位置的估计（插值或平滑）。

滤波算法示意图

11【MATLAB】HANTS滤波算法

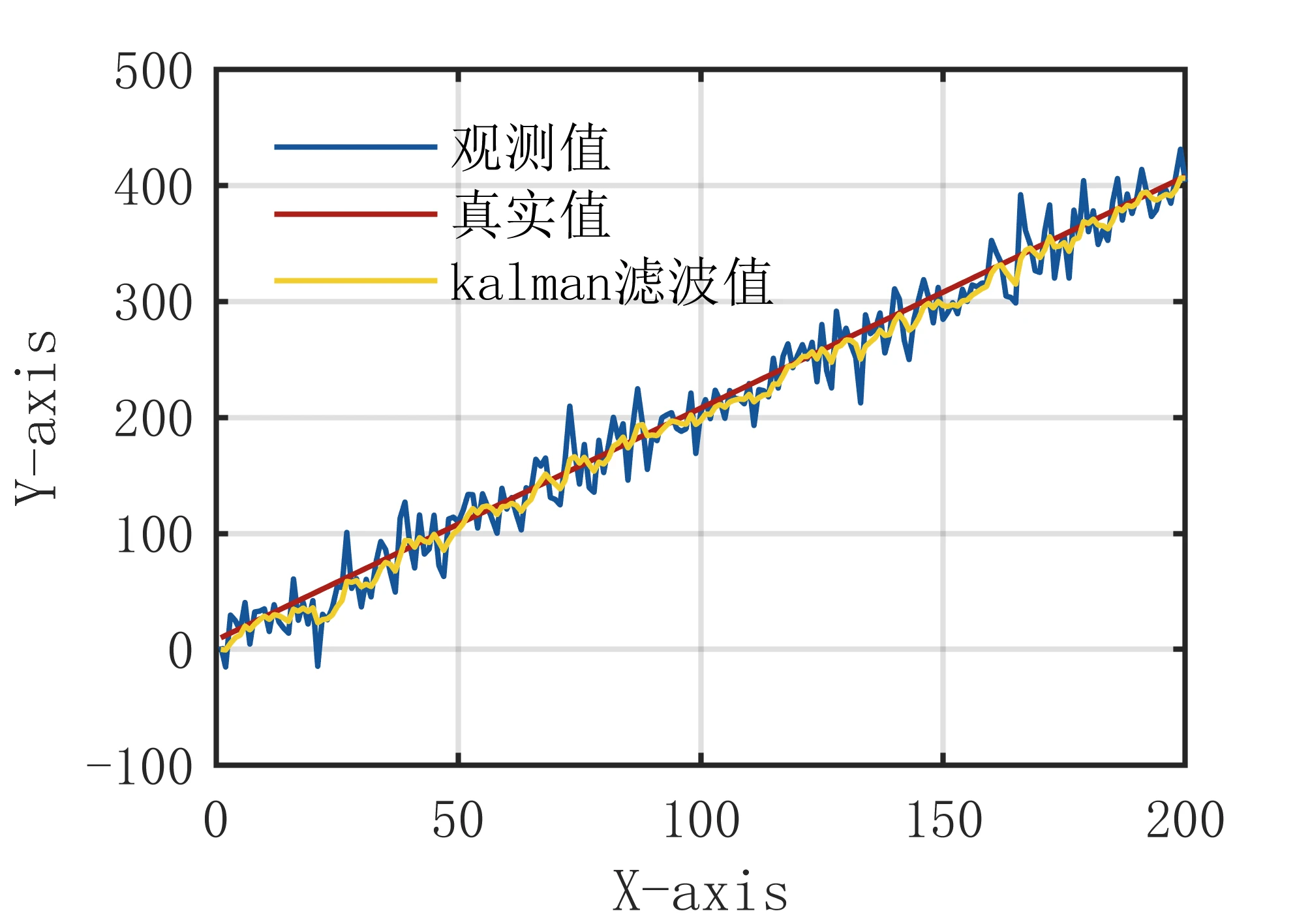
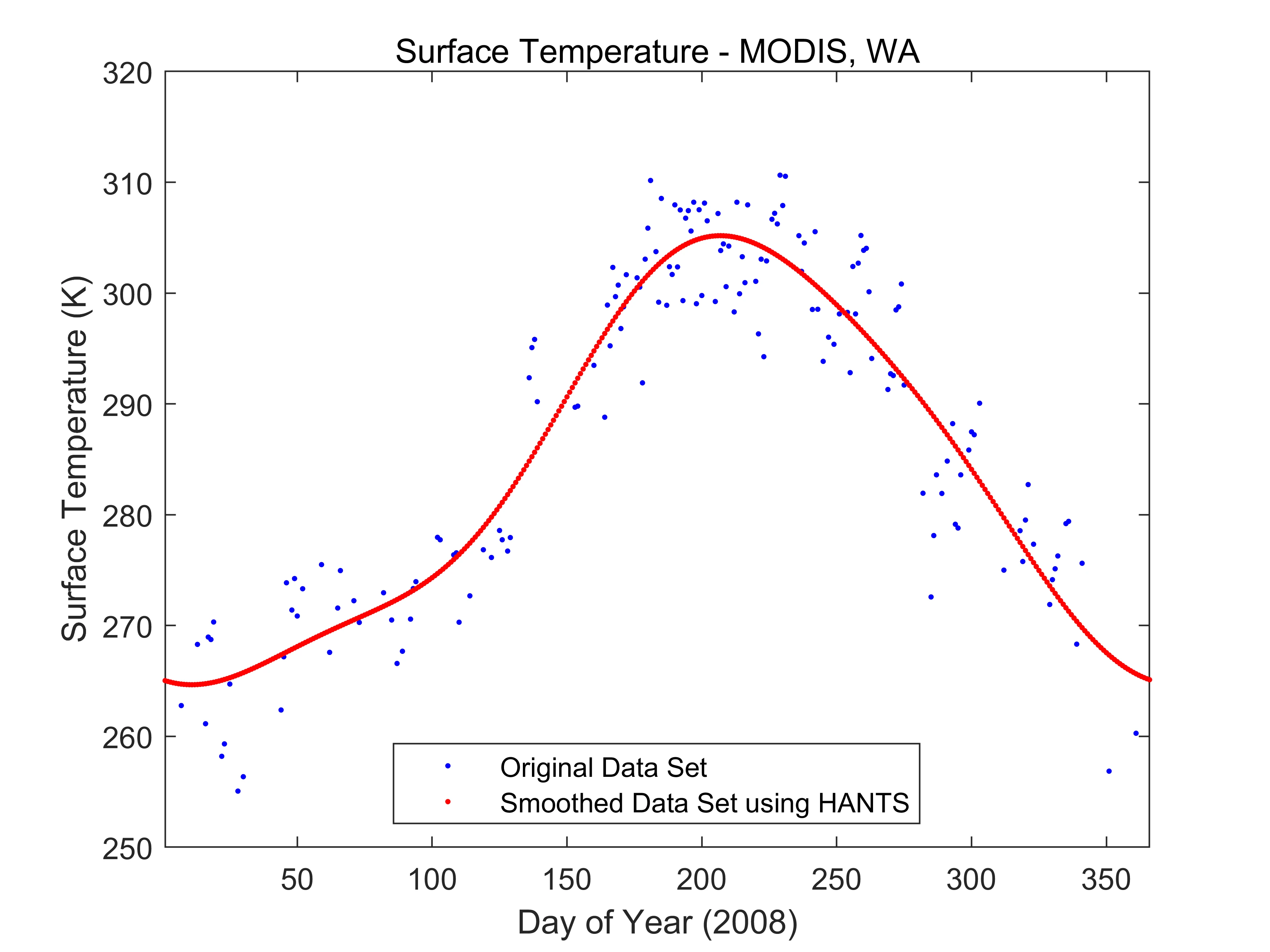
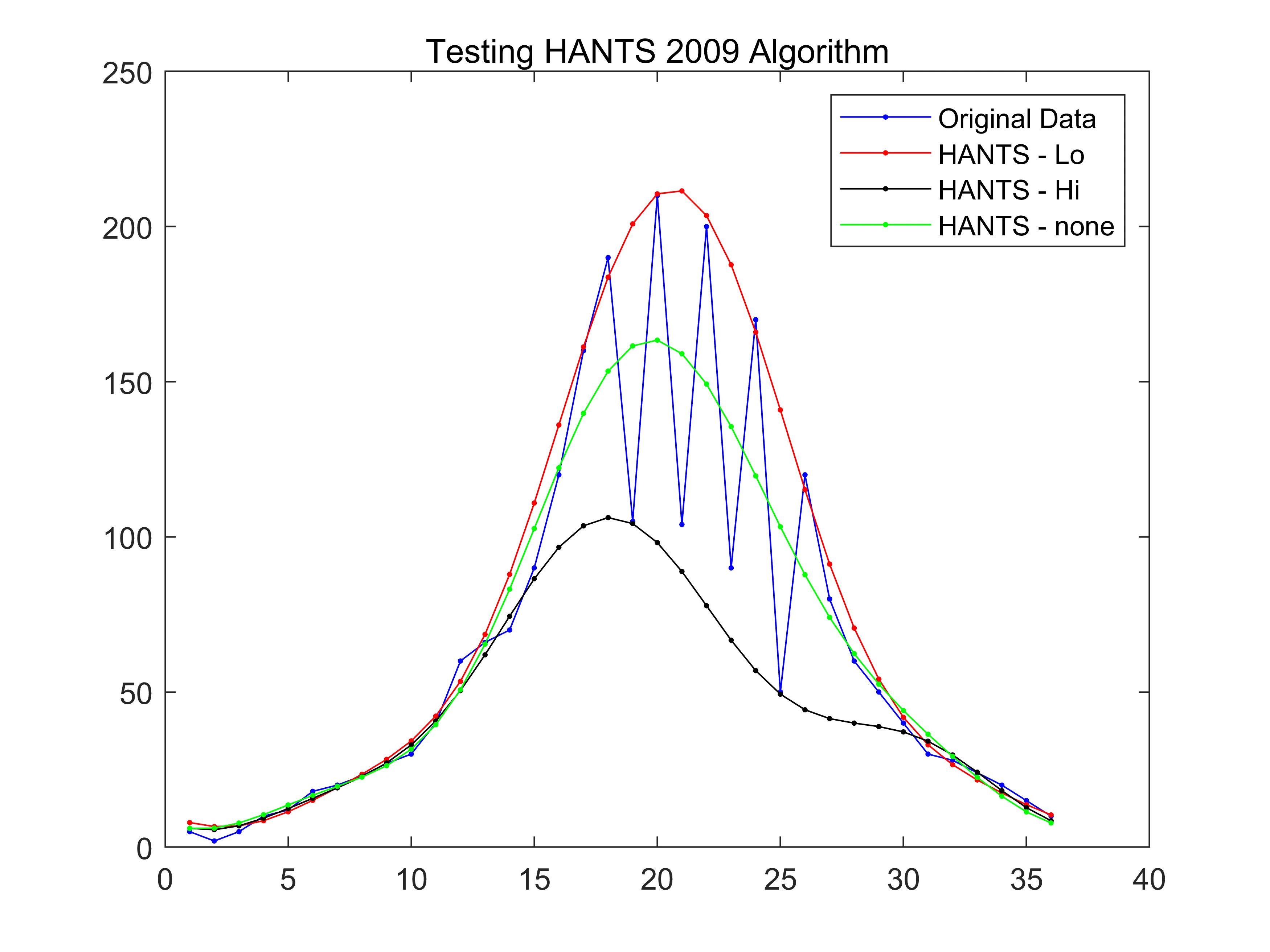
HANTS滤波算法是一种时间序列谐波分析方法，它综合了平滑和滤波两种方法，能够充分利用遥感图像存在时间性和空间性的特点，将其空间上的分布规律和时间上的变化规律联系起来。该算法在进行影像重构时，充分考虑了植被生长周期性和数据本身的双重特点，能够用代表不同生长周期的植被频率曲线重新构建时序NDVI影像，真实反映植被的周期性变化规律。

HANTS滤波算法对快速傅立叶变换进行了改进，具有更大的灵活性。具体来说，它可以是不等时间间隔的影像，同时对时序图像的要求不象快速傅立叶变换（FFT）那么严格。该算法的核心算法是最小二乘法和傅立叶变换。通过最小二乘法的迭代拟合去除时序NDVI值中受云污染影响较大的点，借助于傅立叶在时间域和频率域的正反变换实现曲线的分解和重构，从而达到时序遥感影像去云重构的目的。

滤波算法示意图

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删