MATLAB神经网络拟合代码详解 MATLAB神经网络拟合函数指南

函数介绍

newlind——设计一个线性层

newlind函数返回的net已经训练完毕，不需要再自行调用train函数训练

最小二乘法演示 newlind拟合直线

登录后复制

x=-5:5;
 y1=3*x-7;				                 % 直线方程
 randn('state',2);			             % 设置种子，便于重复执行
 y=y1+randn(1,length(y1))*1.5;% 加入噪声的直线
 plot(x,y,'o',x,y1,'-');
 

‘函数与噪声’

登录后复制

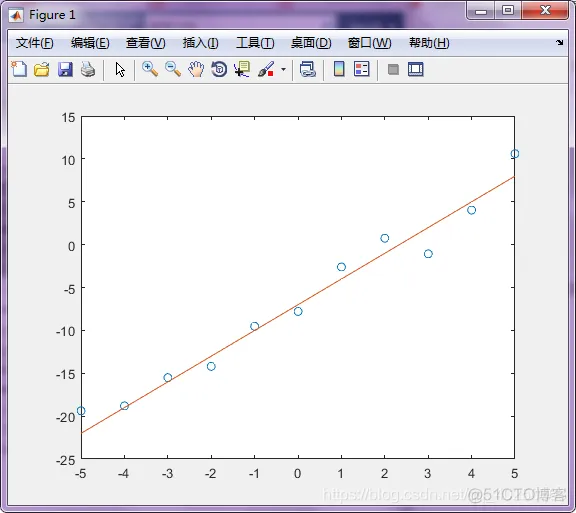
x=-5:5;
 y=3*x-7;				    % 直线方程
 randn('state',2);			% 设置种子，便于重复执行
 y=y+randn(1,length(y))*1.5;% 加入噪声的直线
 plot(x,y,'o');
 P=x;T=y;
 net=newlind(P,T);			% 用newlind建立线性层
 new_x=-5:.2:5;			    % 新的输入样本
 new_y=sim(net,new_x);		% 仿真
 hold on;plot(new_x,new_y);
 legend('原始数据点','最小二乘拟合直线');
 net.iw				
 net.b					
 title('newlind用于最小二乘拟合直线');
 

（（（（'state’是对随机发生器的状态进行初始化，并且定义该状态初始值。比如你过一段时间还要使用这个随机数的时候，还能保持当前的随机取值。

比如

randn(‘state’,2013)

a = randn(1)

b = randn(1) 会发现与上一个随机值不一样

如果再定义一次

randn(‘state’,2013)

c = randn(1) 会发现与a的值一样））））

newlin——构造一个线性层 。

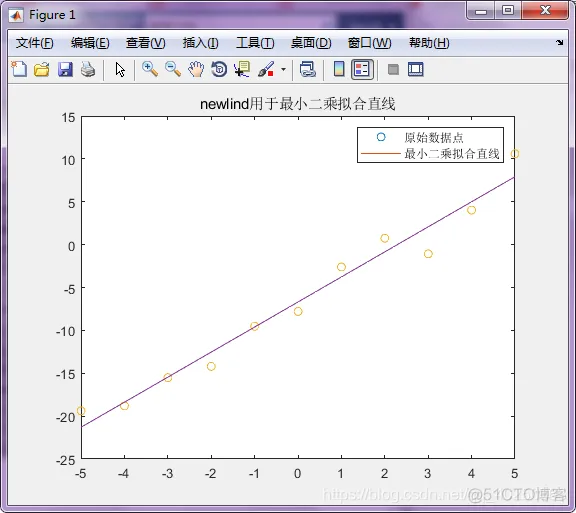
newlin函数用于创建一个未经训练的线性神经网络。输入参数格式如下

登录后复制

%% 程序
 x=-5:5;
 y=3*x-7;				% 直线方程为 
 randn('state',2);			% 设置种子，便于重复执行
 y=y+randn(1,length(y))*1.5;		% 加入噪声的直线
 plot(x,y,'o');
 P=x;T=y;
 net=newlin(minmax(P),1,[0],maxlinlr(P));	% 用newlin创建线性网络  %maxlinlr  计算最大学习率，表达式有待查找。。。 
 tic;net=train(net,P,T);toc		% tic 计时开始 toc 计时结束
 new_x=-5:.2:5;            %更新测试集
 new_y=sim(net,new_x);		% 仿真
 hold on;plot(new_x,new_y);
 legend('原始数据点','最小二乘拟合直线');
 title('newlin用于最小二乘拟合直线');
 net.iw %显示网络的参数，可自行查找
 net.b
 

learnwh

登录后复制

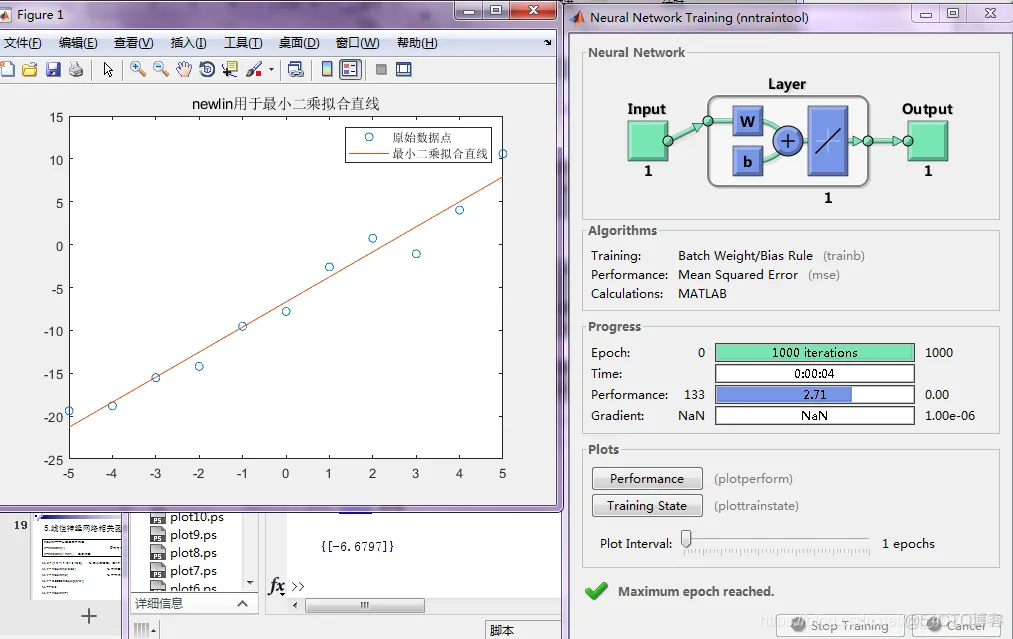
%% 清理
clear,clc
close all

%% 定义数据
P=-5:5;                         % 输入：11个标量
d=3*P-7;
randn('state',2);	
d=d+randn(1,length(d))*1.5     % 期望输出：加了噪声的线性函数

P=[ones(1,length(P));P]        % P加上偏置
lp.lr = 0.01;                  % 学习率
MAX = 150;                     % 最大迭代次数
ep1 = 0.1;                     % 均方差终止阈值
ep2 = 0.0001;                  % 权值变化终止阈值
%% 初始化
w=[0,0];
 
%% 循环更新
 for i=1:MAX
    fprintf('第%d次迭代：\n', i)
    e=d-purelin(w*P);          % 求得误差向量
    ms(i)=mse(e);              % 均方差
    ms(i)
    if (ms(i) < ep1)           % 如果均方差小于某个值，则算法收敛
        fprintf('均方差小于指定数而终止\n');
       break; 
    end
    dW = learnwh([],P,[],[],[],[],e,[],[],[],lp,[]);    % 权值调整量
    if (norm(dW) < ep2)        % 如果权值变化小于指定值，则算法收敛
       fprintf('权值变化小于指定数而终止\n');
       break;
    end
    w=w+dW                     % 用dW更新权值   
 end
 
%% 显示
fprintf('算法收敛于：\nw= (%f,%f),MSE: %f\n', w(1), w(2), ms(i));
figure;
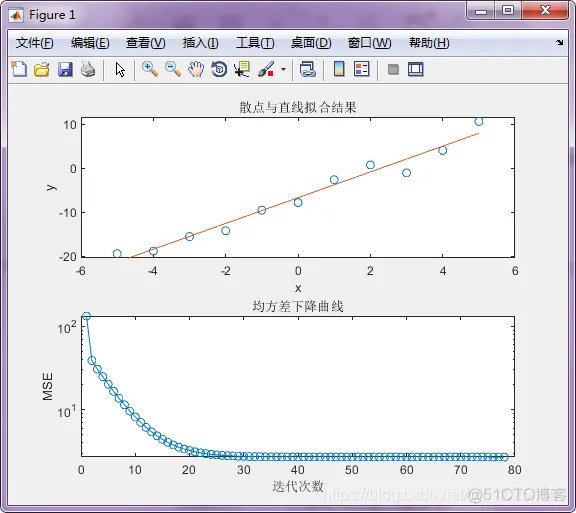
subplot(2,1,1);                % 绘制散点和直线
plot(P(2,:),d,'o');title('散点与直线拟合结果');
xlabel('x');ylabel('y');
axis([-6,6,min(d)-1,max(d)+1]);
x1=-5:.2:5;
y1=w(1)+w(2)*x1;
hold on;plot(x1,y1);
subplot(2,1,2);                % 绘制均方差下降曲线
semilogy(1:i,ms,'-o');         %对数曲线图
xlabel('迭代次数');ylabel('MSE');title('均方差下降曲线');

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删