径向基函数(Radial Basis Function,RBF)神经网络是一种传统的神经网络,于1988年首次被提出。1989年,Jackson论证了RBF神经网络对非线性连续函数的一致逼近性能。
RBF神经网络有很强的逼近能力、分类能力和学习速度。其工作原理是把网络看成对未知函数的逼近,任何函数都可以表示成一组基函数的加权和,也即选择各隐层神经元的传输函数,使之构成一组基函数来逼近未知函数。RBF人工神经网络由一个输入层、一个隐含层和一个输出层组成。
RBF神经网络结构简单、训练简洁且收敛速度快,能够逼近任意非线性函数,因此被广泛应用于时间序列分析、模式识别、非线性控制和图形处理等领域。
以下内容主要参考了《MATLAB神经网络43个案例分析》第7章。
RBF神经网络的神经元模型如图所示。径向基神经网络的节点激活函数采用径向基函数,通常定义为空间任一点到某一中心之间的欧式距离的单调函数。
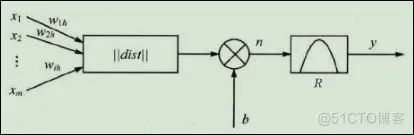
图中所示的径向基神经元结构可以看出,径向基神经网络的激活函数是以输入向量x和权值向量w之间的距离Il dist ll作为自变量的。径向基神经网络的激活函数R的一般表达式为

随着权值和输入向量之间距离的减少,网络输出是递增的,当输入向量和权值向量一致时,神经元输出为1。图中的b为阈值,用于调整神经元的灵敏度。利用径向基神经元和线性神经元可以建立广义回归神经网络,此种神经网络适用于函数逼近方面的应用;径向基神经元和竞争神经元可以建立概率神经网络,此种神经网络适用于解决分类问题。由输入层、隐藏层和输出层构成的一般径向基神经网络结构如下图所示。在RBF神经网络中,输入层仅仅起到传输信号的作用,与传统的神经网络相比,输入层和隐含层之间可以看作连接权值为1的连接,输出层和隐含层所完成的任务是不同的,因而它们的学习策略也不相同。输出层是对线性权进行调整,采用的是线性优化策略,因而学习速度较快。而隐含层是对激活函数(格林函数或高斯函数,一般取高斯函数)的参数进行调整,采用的是非线性优化策略,因而学习速度较慢。

以下内容参考了mathworks官网文档Radial Basis Neural Networks对几个函数的介绍,以及函数各自的介绍文档。
radbas函数为径向基传递函数,其调用格式为
A = radbas(N,FP)
其中 N为输入向量组成的S×Q维矩阵; FP为函数参数的结构(忽略); A为函数返回矩阵,与N一一对应,即N中的每个元素通过径向基函数得到A;
newrb()函数可以设计一个近似径向基网络,其调用格式为
[net,tr] = newrb(P,T,goal,spread,MN,DF)
其中 P为Q组输入向量组成的R×Q维矩阵; T为Q组目标分类向量组成的S×Q维矩阵; goal为均方误差目标(Mean Squared Error Goal),默认为0; spread为径向基函数的扩展速度,默认为1; MN为神经元的最大数目,默认为Q; DF为两次显示之间所添加的神经元数目,默认为25; net为返回值,即一个RBF网络; tr为返回值,训练记录。
用newrb()创建RBF网络是一个不断尝试的过程,在创建过程中,需要不断增加中间层神经元的个数,直到网络的输出误差满足预先设定的值或者达到最大神经元数量为止。该函数设计的径向基网络net可用于函数逼近。径向基函数的扩展速度spread越大,函数的拟合就越平滑。但是,过大的spread意味着需要非常多的神经元以适应函数的快速变化。如果spread设定过小,则意味着需要许多神经元来适应函数的缓慢变化,这样一来,设计的网络性能就不会很好。对于特定问题,需要多次尝试寻找最好的网络结构。
newrbe函数用于设计一个精确径向基网络,其调用格式为
net = newrbe(P,T,spread)
其中, P为Q组输入向量组成的R×Q维矩阵; T为Q组目标分类向量组成的S×Q维矩阵; spread为径向基函数的扩展速度,默认为1。 和newrb()不同,newrbe()能够基于设计向量快速、无误差地设计一个径向基网络。
Radial Basis Approximation是利用RBF进行函数拟合的示例,并进行了详细的介绍,但是对我没啥用,只把链接放在这里。Radial Basis Underlapping Neurons和Radial Basis Overlapping Neurons研究了扩散常数如何影响径向基网络的设计过程。
代码来源为Classification by Radial Basis Function Neural Networks,使用newrb函数建立的RBF神经网络对三分类问题进行训练和测试,具体过程见代码注释。
%% 网络的构建和训练
% 训练数据,输入为9*3的矩阵,9个输入,带有3个特征
data = [10 0 0;
10 0 1;
10 1 0;
2 10 0;
2 10 1;
2 11 0;
5 0 10;
5 0 11;
5 1 10];
% 从输出目标可以看到输入分为3类
target = [1;1;1;2;2;2;3;3;3];
% 利用数据构建RBF神经网络并训练
net = newrb(data',target'); % 注意矩阵的转置
save('net.mat','net'); % 将网络net保存为.mat文件,后面可直接调用
% 查看效果
y = sim(net,data'); % 网络对输入进行运算得到输出y
y=round(y); % 将输出y的近似值作为分类结果
performance = sum(target==y')/size(target,1) % 计算网络输出和实际输出的对应程度
%% 测试训练后的模型
load('net.mat'); % 导入之前保存的网络
testdata = [10 0 0]; % 给出一个新的数据
y = sim(net,testdata'); % 利用训练后的网络对新数据进行分类
y=round(y); % 得到分类结果
运行结果,会给出网络的均方根误差MSE,以及准确率performance,这里的效果还是很好的。
NEWRB, neurons = 0, MSE = 0.666667
performance =
1
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删