1 概述
在ANSYS计算过程中,有时候会遇到不同单元之间进行连接,由于不同的单元自由度不同,连接时通常需要通过耦合和约束方程建立节点自由度的关系,保证结果的准确性。
耦合可以理解成是将耦合的对象某个自由度作相等处理,而约束方程则不局限于相等这个关系,其可以描述具有某种关系的自由度。如图1所示,为梁单元与平面单元的连接。如果不采用约束方程,力矩的传递无法完成,因为平面单元没有转动自由度。
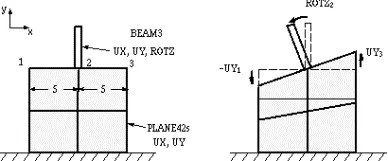
图1 梁单元与平面单元连接
为使节点2具有力矩传递的能力,要求1、2、3节点之间的自由度满足以下关系:
ROTZ2 = (UY3 - UY1)/10
再通过CE命令,即可将此关系通过约束方程的形式施加给1、2、3节点。
2 命令
查看ANSYS的帮助文档,查询CE命令的解释,如图2所示。

图2 ANSYS的CE命令解释
CE, NEQN, CONST, NODE1, Lab1, C1, NODE2, Lab2, C2, NODE3, Lab3, C3
其中,NEQT表示常数,用于区别约束方程,一般可以用数字1、2、3表示即可,表示第几个约束方程;
CONST表示方程的常数项,一般为0;
NODE1,表示第一个节点;
Lab1,表示自由度标签,对于结构而言,就是三个平移和三个转动自由度;
C1,表示该自由度的系数;
同理,后面的也一样。
对于方程ROTZ2 = (UY3 - UY1)/10
稍作变形,0 = UY3 - UY1 - 10*ROTZ2
由此式即可直接写出对应的ANSYS命令流:
CE,1,0,3,UY,1,1,UY,-1,2,ROTZ,-10
3 模型
本次为梁单元与实体单元的连接,建立模型,如图3所示,梁单元与实体单元有一个节点位置重合,为使位移和力矩能够传递,需要耦合两个节点的三个平移自由度,同时还需要用约束方程限制梁的三个转动自由度。
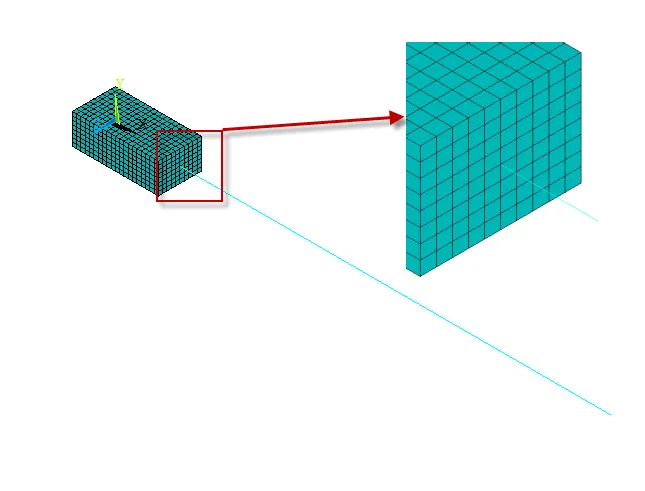
图3 梁单元与实体单元
4 约束方程
节点自由度耦合比较好操作,采用CP命令,重合位置处的两个节点分别为节点1(梁)和节点21(实体),自由度耦合如下:
CP,1,UX,1,21 !耦合节点1和节点21X方向自由度
CP,2,UY,1,21 !耦合节点1和节点21Y方向自由度
CP,3,UZ,1,21 !耦合节点1和节点21Z方向自由度
为约束转动自由度,由CE的参数项可知,需要先写出转动约束方程,对照图4分别写出三个转动自由度的约束方程,图4中红圈的四个节点分布在中心节点周围,将这几个节点进行约束即可限制梁单元和实体单元的转动自由度,自由度方程如下:
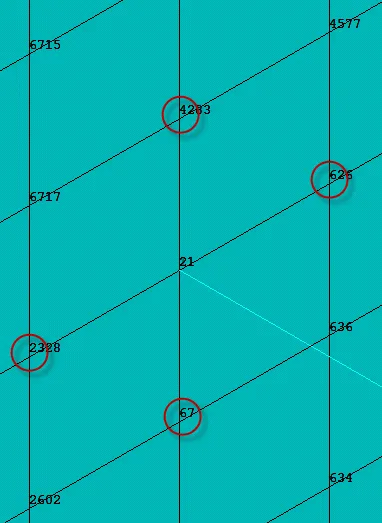
图4 节点分布
ROTY(1)=(UX(626)-UX(2328))/ABS(NZ(626)-NZ(2328)) !Y轴转动
ROTZ(1)=(UX(67)-UX(4283))/ABS(NY(67)-NY(4283)) !Z轴转动
ROTX(1)=(UZ(67)-UZ(4283))/ABS(NY(67)-NY(4283)) !X轴转动
稍作变换如下:
0=(UX(626)-UX(2328))- ROTY(1)*ABS(NZ(626)-NZ(2328))
0=(UX(67)-UX(4283))- ROTZ(1)* ABS(NY(67)-NY(4283))
0=(UZ(67)-UZ(4283))- ROTX(1)* ABS(NY(67)-NY(4283))
对应的CE命令为:
CE,1,0,626,UX,1,2328,UX,-1,1,ROTY,-ABS(NZ(626)-NZ(2328)) CE,2,0,67,UX,1,4283,UX,-1,1,ROTZ,-ABS(NY(67)-NY(4283)) CE,3,0,67,UZ,1,4283,UZ,-1,1,ROTX,-ABS(NY(67)-NY(4283))
施加完成后如图5所示。

图5 施加耦合、约束方程之后
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删