材料力学探索：ANSYS特征值屈曲分析在压杆稳定中的应用

导读：掌握压杆不同约束条件的施加和特征值屈曲分析方法，临界载荷等于施加的载荷乘以特征值。

一、模型演示

以下模型实验演示了不同边界条件下受压杆件的屈曲现象和对应的屈曲变形。实验中采用塑料尺来模拟杆件，我们可以感受到使塑料尺发生屈曲时所需力的大小。

(1)将塑料尺的一端置于桌面上，另一端用手掌加以固定，下压塑料尺的顶部并逐步增加压力，直尺会突然产生如图a所示的侧向变形。进一步增加压力，变形也会相应的增大。本实验演示了两端铰支杆件的屈曲现象。

图a  两端铰支

2)用手指将塑料尺的两端捏紧，防止其发生选装和平动。然后对直尺逐渐施加压力直至出现如图b所示的侧向变形。本实验演示了两端固定杆件的屈曲现象。可以明显感受到本实验所需的临界压力要大于前一个实验。

图b 两端固定

3)如果在塑料尺中部设置一侧向支撑，以保证尺子在这点不会发生平动，则需要施加比第一个实验更大的压力才能使塑料尺发生如图c所示的屈曲变形。

图c 中部侧向支撑

模型演示图片来源：英国曼彻斯特大学季天健教授。

二、定义和概念

稳定性：平衡物体在其原来平衡状态下抵抗干扰的能力。

失稳：不稳定的平衡物体在任意微小的外界干扰下的变化或破坏过程，也称为屈曲。

临界载荷：使结构介于稳定平衡和不稳定平衡之间的载荷，或使结构处于屈曲临界状态的载荷。

平衡的三种状态：稳定平衡、随遇平衡（临界状态）、不稳定平衡。

三、问题描述

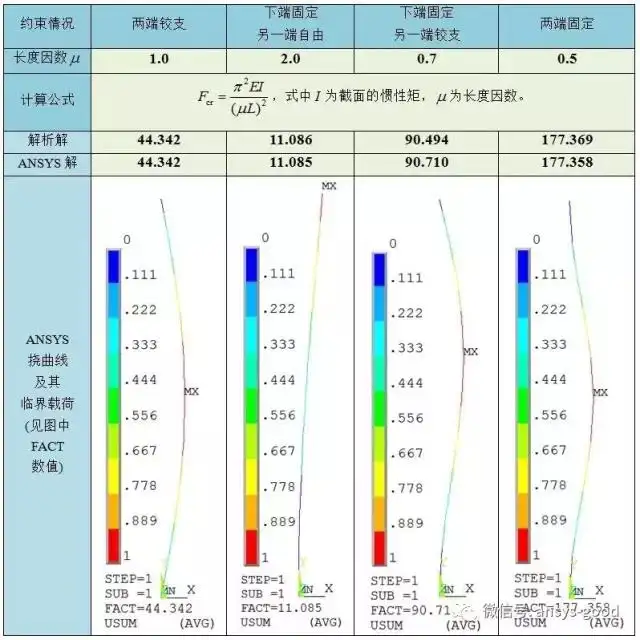
钢板尺子长度500mm，宽度39mm，厚度1.2mm。弹性模量E= 200 GPa，泊松比u =0.3。

分别受以下4种约束作用：

(1)两端铰支，

(2)一端固定、另一端自由，

(3)一端固定、另一端铰支，

(4)两端固定。

计算在各种约束情况下的临界载荷。

问题分析：对于这4种约束作用，对应的边界条件见下图所示。

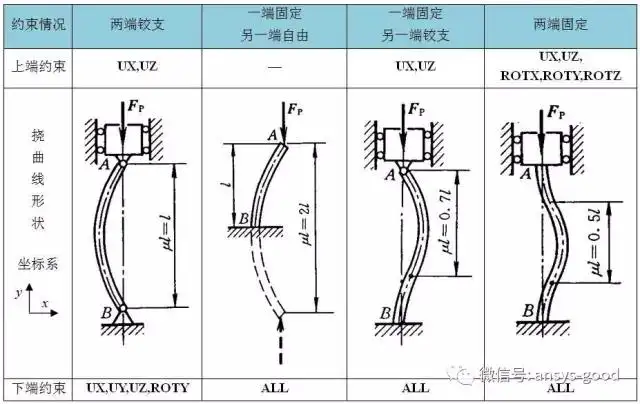
临界载荷计算结果：

四、APDL步骤

Ex=2e5      !弹性模量MPa

b=1.2        !截面宽度mm

h=39        !截面长度mm

Len=500     !压杆长度mm

I=h*b**3/12            !惯性矩

pi=ACOS(-1)

miu=1                                            !长度因数

Fcr=pi**2*Ex*I/(miu*Len)**2     !第1阶失稳载荷解析解

/PREP7  

ET,1,BEAM188        !单元类型

KEYOPT,1,3,3         !形函数

SECTYPE,   1, BEAM, RECT, , 0    !截面属性

SECOFFSET, CENT

SECDATA,1.2,39,0,0,0,0,0,0,0,0,0,0

MP,EX,1,2e5            !材料属性

MP,PRXY,1,0.3

K,1,0,0,0,                 !创建关键点

K,2,0,500,0

L,1,2                           !创建直线

LESIZE,1,50, , , , , , ,1    !单元尺寸mm

LMESH,1                              !分网

DK,1,UX               !下端铰支

DK,1,UY

DK,1,UZ

DK,1,ROTY

DK,2,UX               !上端铰支

DK,2,UZ

FK,2,FY,-1              !施加单位载荷

FINISH

/SOLU

PSTRES,1         !打开预应力

SOLVE               !求解

FINISH               !退出求解器

/SOLU

ANTYPE,1              !分析类型-特征值屈曲

BUCOPT,SUBSP,1,0,0     !特征值屈曲分析选项SUBOPT,0,0,0,0,0,ALL

MXPAND,1,0,0,0,0.001,    !扩展模态数

SOLVE                                     !求解

FINISH

/POST1

SET,LIST                          !列表查看特征值

/GFORMAT,F,12,3,          !数据格式

/DSCALE,ALL,30             !变形比例

PLNSOL, U,SUM, 0,1.0    !屈曲变形

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删