1、非线性问题

按照力学微分方程和边界条件的分类，可以把非线性问题分为：

·几何非线性

·材料非线性

·接触非线性

其中：

·几何非线性一般指大变形，或称之为有限变形理论。有些情况下，也将压杆稳定问题或屈曲分析归入几何非线性中。

·材料非线性指本构关系的非线性，如弹塑性材料、超弹性材料、各向异性材料等。

·接触非线性也可理解为边界条件的非线性，如光滑平面边界、摩擦接触、非线性弹簧等。

线性和非线性问题在数学上通常会归结于求解微分方程，而非线性微分方程不同于线性微分方程可以直接求解，它是无法直接解的超越方程，一般通过迭代法计算它的数值解。这也是非线性计算量远大于线性计算的原因。

2、什么时候需要打开大变形

因为非线性求解的不经济性，在可以采用线性计算的时候，推荐使用线性方法。那么，该怎样去判断呢？出于直观判断：当应变较大时，再使用大变形。这个判断当然也是正确的，但这只是打开大变形的充分条件，这里需要注意的是：小应变时也有可能需要打开大变形。

在ANSYS帮助文档的解释中，包含了以下4种情形需要打开大变形：

1. 大应变-Large strain
2. 大转角-Large rotation
3. 应力刚化-Stress stiffening
4. 自旋软化-Spin sortening

其中，大应变的例子在上一篇已经操作过了，接下来将通过几个例子大致概述一下剩下的情形。

3、大转角-Large Rotation

举一个非常极端的例子，一个梁的一端旋转90°，整个梁没有应变。ANSYS中设置如下所示：

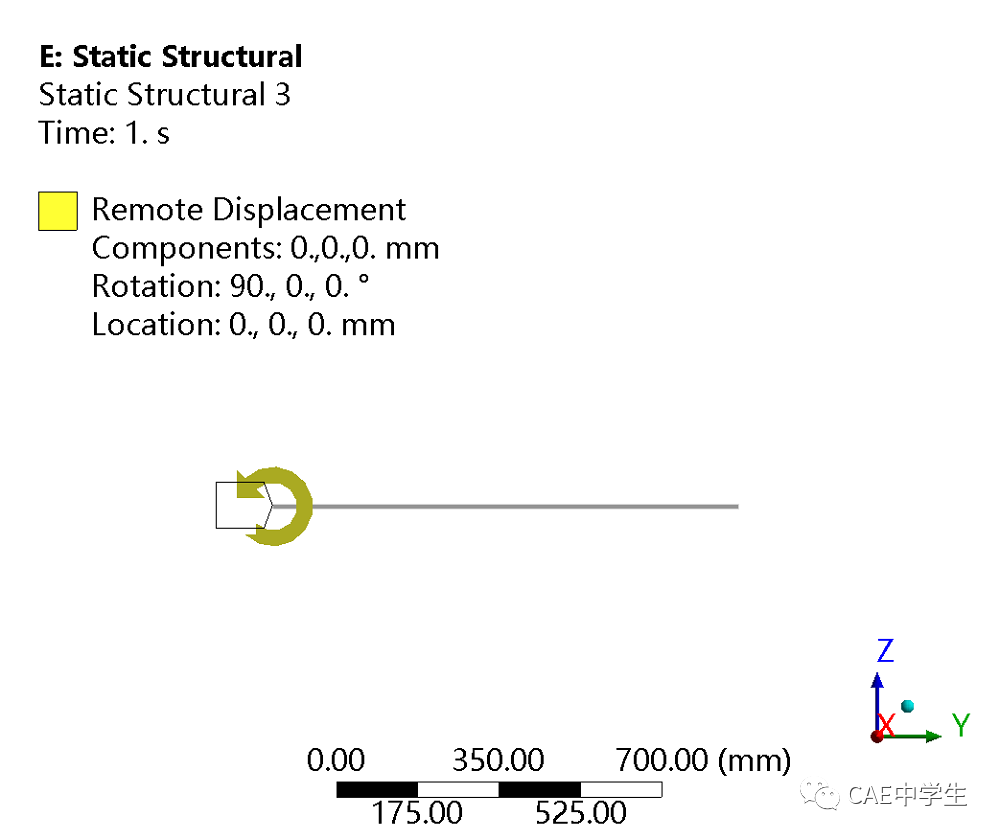
不打开大变形和打开大变形的总变形结果对比如下：

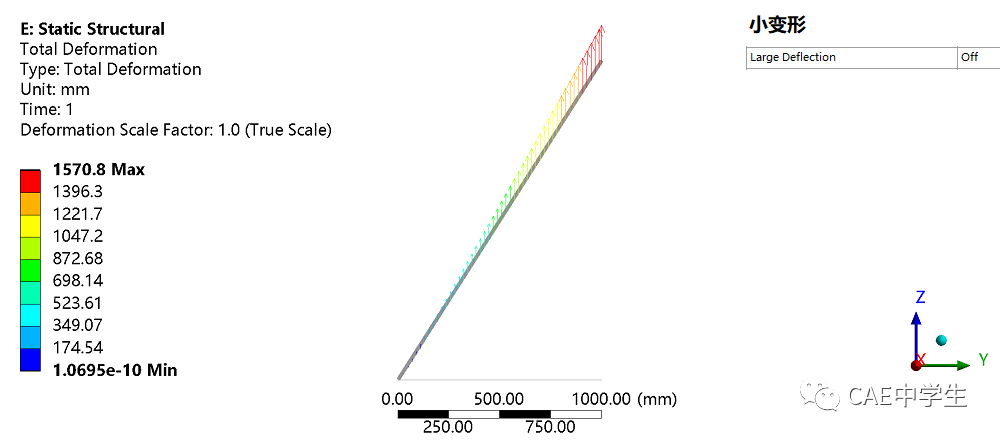
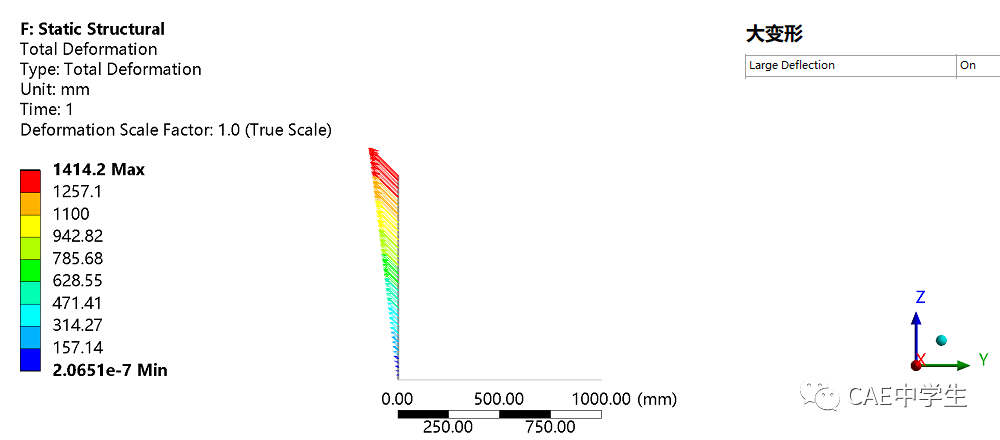
可以看出，旋转在小应变假设中简化为方向始终在初始旋转切向上的平动，可见当计算场景有了较大转角时，应注意考察小应变假设引起的误差是否在可接受范围内。

第二个例子是悬臂梁在面压力作用下的变形。和上述情况相似，面压力在小应变假设中简化为方向始终在受压面初始法向的载荷。下图显示结果为梁截面上的反力。

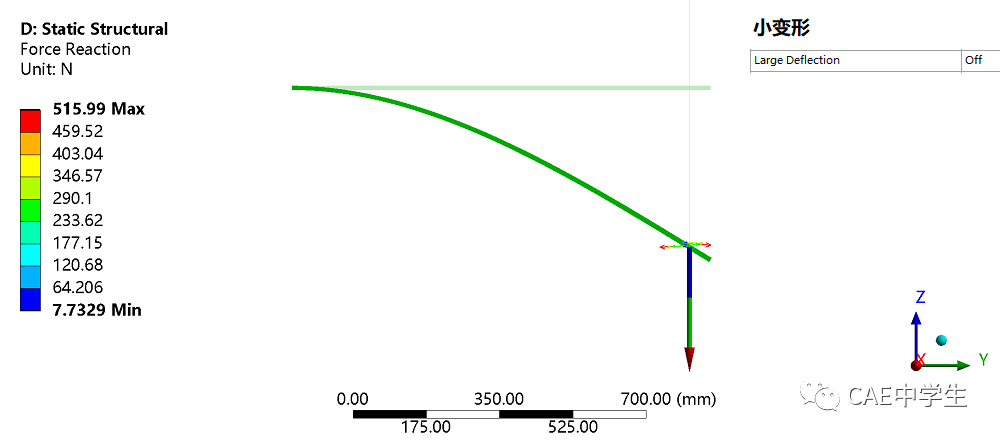
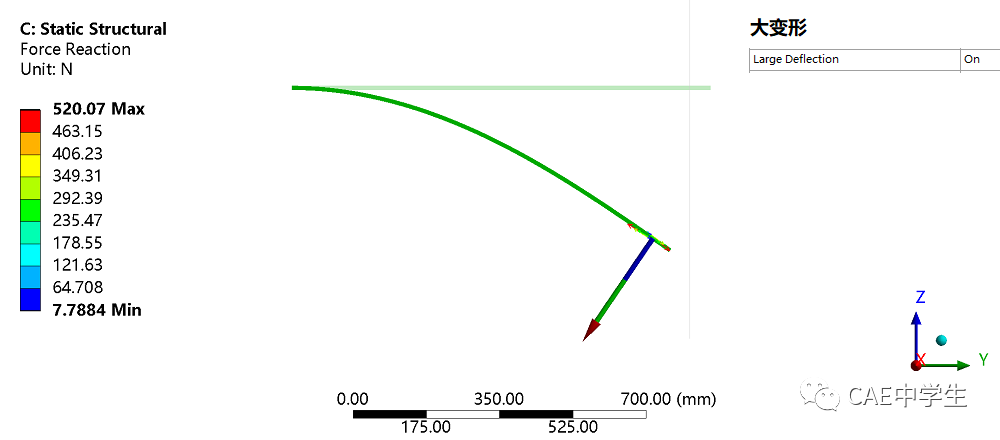
总而言之，当计算涉及节点矢量位移方向的改变时，如旋转位移、可变形面上的压力载荷、铰支边界等，都应该考虑到线性分析不会迭代计算的特点，即结构自身在变形后同时改变载荷或约束方向的效应是会被忽略的。

4、应力刚化-Stress Stiffening

所谓应力刚化就是指结构的纵向张力对横向刚度的加强效应，几乎所有弦乐的乐器都是利用了这个效应来得到不同的音调。

举一个例子，一个梁两端完全固定，中间受剪力，如下所示：

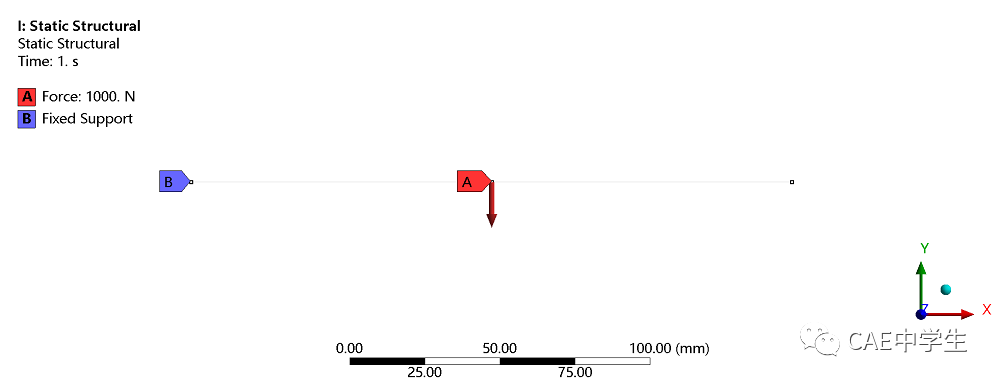
根据应力刚化效应，随着载荷的不断增大，梁内张力逐渐增大，梁的刚度同时也在增大，这样一来力-变形曲线应当是斜率随着力增大而逐渐减小的一条曲线。简单来说，在应力刚化的计算情景中，小变形假设计算得出的结果刚度偏小、变形偏大。计算结果对比如下：

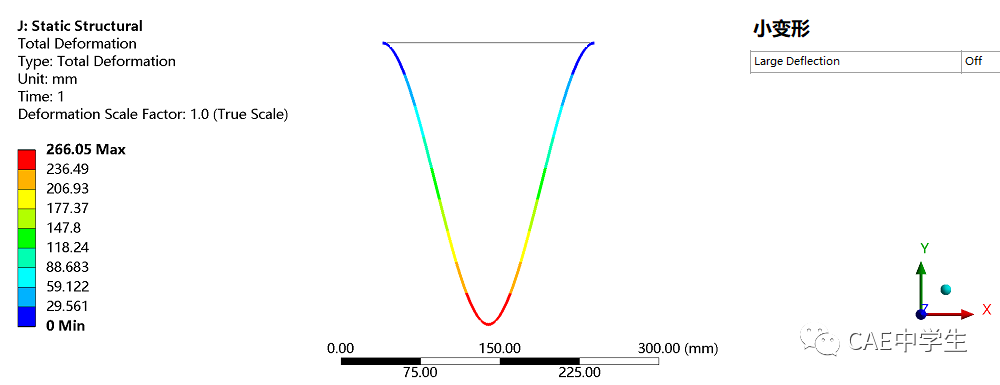
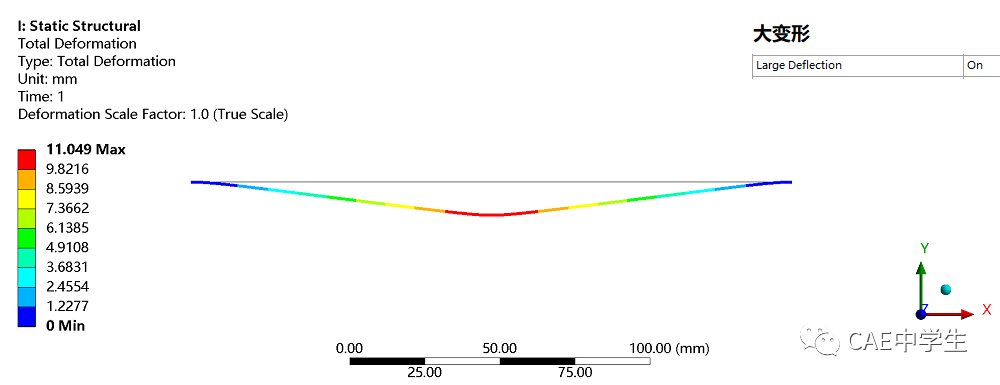
在打开大变形后，时间(力)-变形曲线如下所示。可以看出，在应力刚化的计算情景中，大变形设置产生的影响非常大。

5、自旋软化-Spin Softening

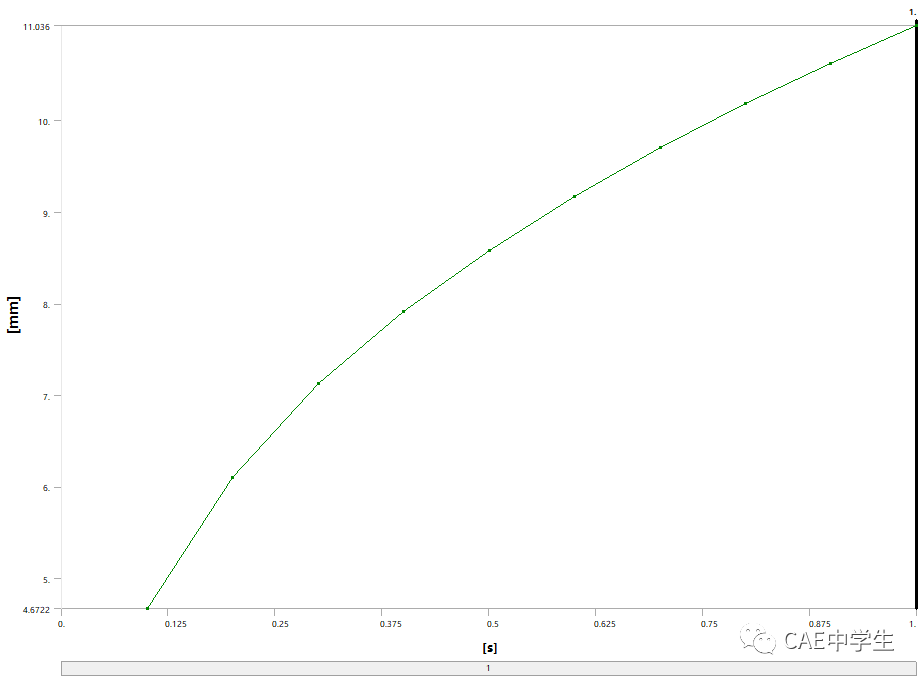
自旋软化指结构自旋对自旋平面径向刚度的削弱现象，其概念与应力刚化有相似之处。不严谨的说，在自旋平面内向外的作用力会得到离心力的帮助，且一旦产生向外的位移，在角速度不变的前提下，离心力会增大，这使得作用力得到了更大的助力，相对来说，这就好像结构在自旋平面内的刚度减小了。

假设一根悬臂梁，一端完全固定，另外一端给一个质点，同时整体在Z轴方向上给一个角速度。

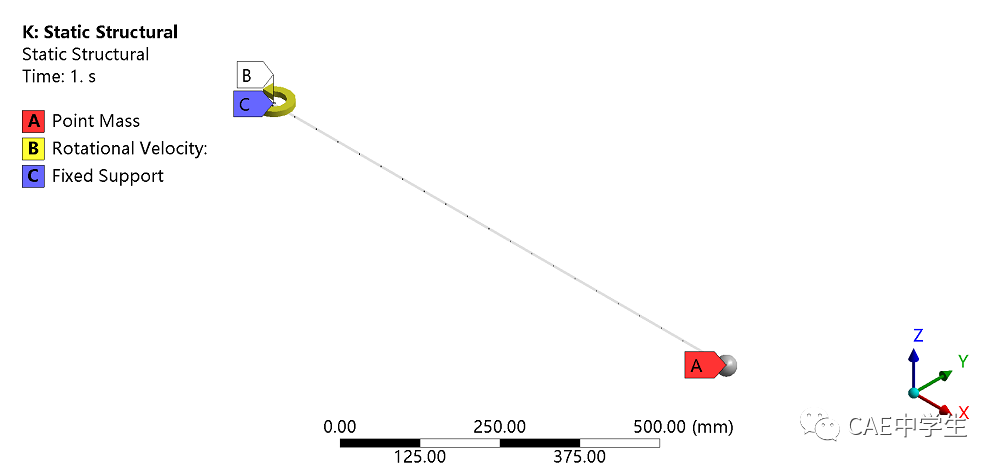
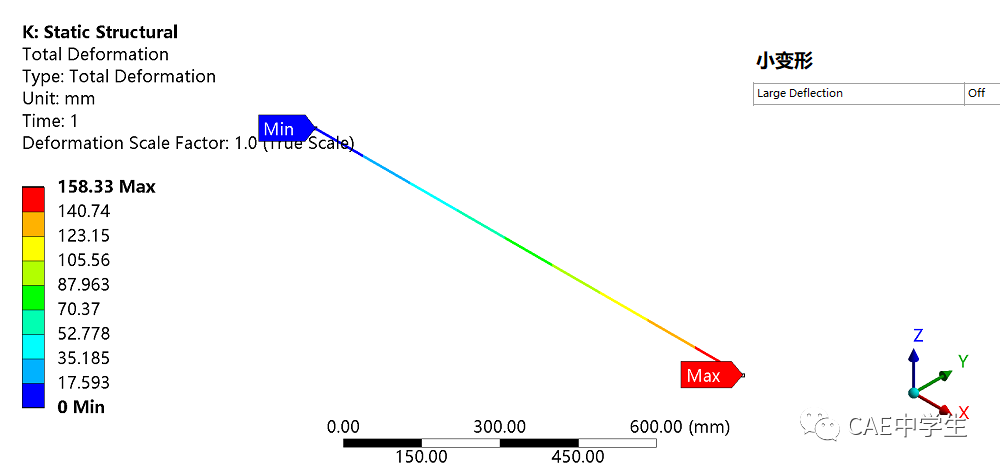
和应力刚化相反，在未打开大变形时，计算结果刚度偏大、变形偏小。

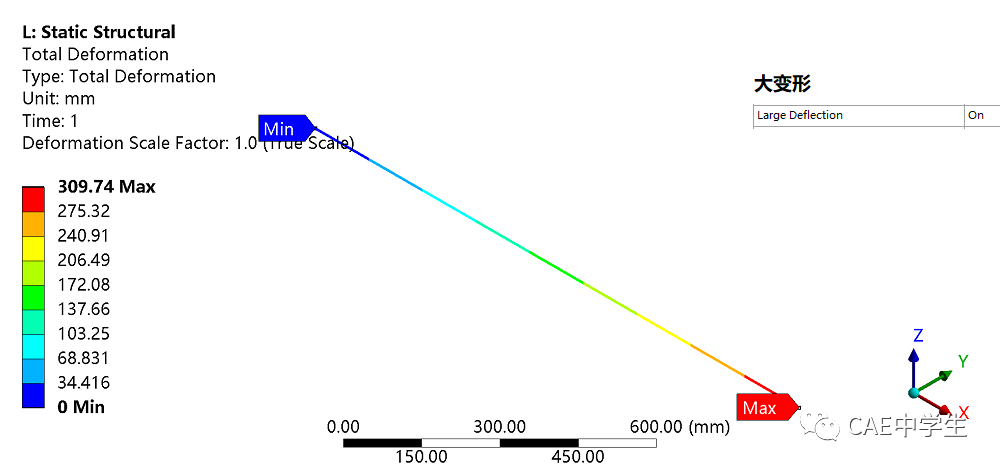
打开大变形后，时间(力)-变形曲线如下所示。

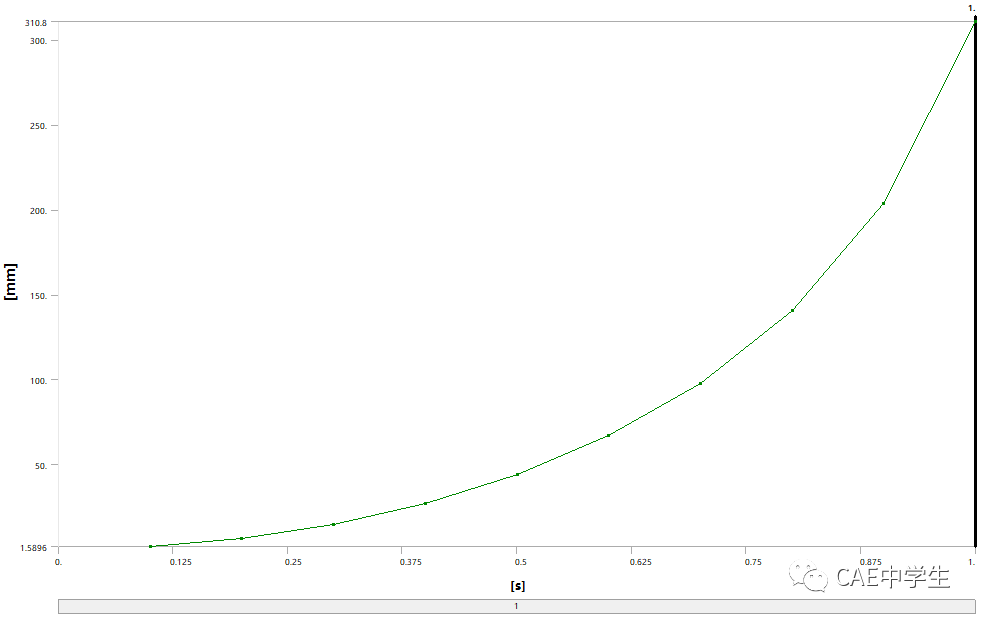
因此，在需要考虑到自旋软化的计算情景下，需要打开大变形设置。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删