ANSYS分析波纹管波形参数对平面失稳的影响

摘要：

为了研究波纹管波形参数对波纹管平面失稳的影响，使用ANSYS软件建立了波纹管的有限元模型，对不同波形参数下的波纹管有限元模型进行了模态分析与特征值屈曲分析。有限元计算结果表明，增加波纹管的壁厚和波距，或者减小波高，会使波纹管的固有频率和屈曲载荷增加，因此在波纹管设计时，在满足综合性能情况下，可通过在一定范围内增加波纹管的壁厚和波距，或者减小波高的方法减少平面失稳的发生；同时模态分析求出了波纹管的固有频率和振型，可以避免在工程作业中，因为外界振动频率与波纹管固有频率相同而发生共振现象，致使波纹管发生平面失稳，为工程设计提供有效参考。

关键词：波纹管;ANSYS数值模拟;屈曲分析;模态分析;波形参数;平面失稳;

0 引言

波纹管膨胀节是用于管道连接和补偿装置，是一种薄壁型壳体，广泛用于航空航天、化工、船舶等领域，它在工作时可补偿由于热胀冷缩和压力变化带来的位移变化，同时还可以起到降噪、减震的作用。在工作中波纹管常会因为内压过大而产生平面失稳，平面失稳一般发生在长度与直径之比较小的波纹管中，或者无加强型波纹管中，是指波纹所在的平面不再与波纹管的轴线保持垂直，一个或多个波纹出现倾斜或弯曲[1]。张庆等[2]提出用ANSYS有限元法对同时承受轴向、横向和转角位移载荷的波纹管进行内压稳定性分析。叶陈等[3]利用 ANSYS软件对未发生位移的波纹管平面失稳压力进行有限元分析。陈晔等[4]用ANSYS有限元软件对U形无加强波纹管在不同平面失稳工况下的应力响应进行了计算。张道伟等[5]对波纹管在拉伸条件下的外压稳定性进行了试验研究和非线性有限元分析。但由于波纹管是薄壁结构，形状不规则，应力也分布较复杂，导致波纹管性能受波形参数影响较大，而波纹参数对平面失稳影响的研究也较少。实际应用中有大量波纹管处于平面失稳状态，所以波纹管的平面稳定性是影响波纹管正常工作能力的一个关键指标。

本文通过ANSYS软件建立了波纹管的有限元模型，对不同尺寸参数下的波纹管有限元模型进行了模态分析与特征值屈曲分析，仿真出在不同波纹参数下波纹管的固有频率和屈曲载荷的变化规律，通过仿真结果分析波纹参数对平面失稳的影响。

1 波纹管的模态分析

模态分析是确定结构振动特性的一种技术，通过它可以确定固有频率和振型。对于一般多自由度的结构系统，任何运动可以由其自由振动的模态合成。有限元的模态分析就是建立模态模型并进行数值分析的过程[6]。

1.1 波纹管几何尺寸及性能参数

本文采用单层波纹管，材料是304不锈钢(0Cr18Ni9),内径510 mm, 波峰半径25 mm, 波谷半径25 mm, 波高50 mm, 波距100 mm, 壁厚1 mm, 波数为6个，波纹管结构图如图1所示。弹性模量为187.4 GPa, 泊松比为0.3,屈服强度为264.4 MPa, 抗拉强度为671.251 MPa, 密度为7.85 g/cm3。

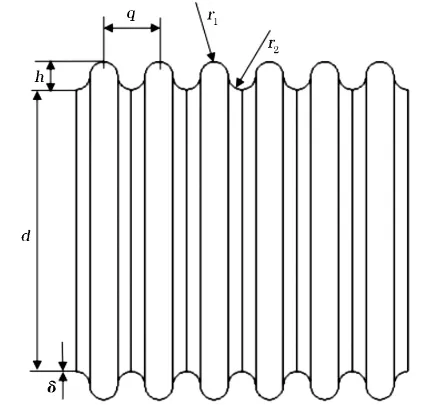
图1 波纹管结构图

1.2 定义材料与网格划分

本文通过Inventor建立波纹管的三维模型，然后将模型导入ANSYS,定义有限元模型的材料属性为304不锈钢，进行网格划分，采取六面体网格，单元类型为shell181,有10 124个节点，10 089个单元。

1.3 模态分析结果

导入模型划分网格后，添加约束，固定波纹管两端，设置求解前6阶振型与固有频率。求解可得前6阶频率分别为142.69、192.41、192.47、196.96、197.12、217.67 Hz。振型如图2～图7所示，可以观察到，当设置约束为两端固定时，波纹管的失稳振型主要表现为平面失稳。

图2 第1阶振型图  

图3 第2阶振型图

图4 第3阶振型图  

图5 第4阶振型图  

图6 第5阶振型图

图7 第6阶振型图

1.4 固有频率随波纹参数变化的规律

在模态模型的基础上，改变波纹管壁厚、波高、波距，对波纹管分别进行模态分析，波纹参数变化后的波纹管振型没有发生变化，固有频率变化情况见图8。

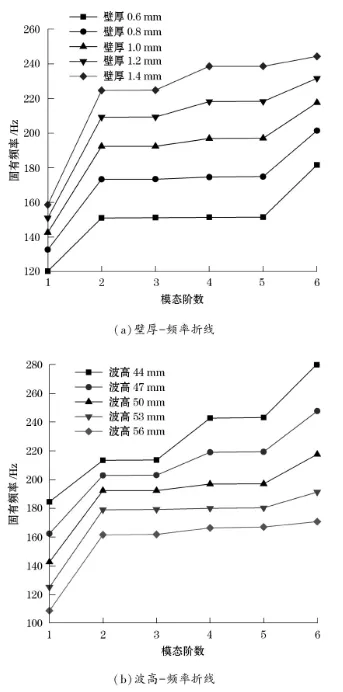
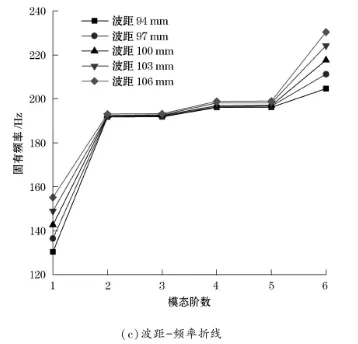
图8 固有频率与波纹参数的关系  

当波纹管的几何参数相同的情况下，波纹管壁厚由0.6 mm增大到1.4 mm, 固有频率随之增大，增大幅度也较明显。当改变波高尺寸，固有频率随尺寸变化的规律与壁厚相反，当波高由44 mm增大到56 mm时，各阶固有频率不断减小。波距的尺寸变化是从94 mm增大到106 mm, 固有频率随尺寸的增大而增大，但是第2阶到第5阶的固有频率增大幅度较小，固有频率几乎相同。

在设计波纹管时，应该考虑工作状态下波纹管的振动频率，从而避免外界振动频率与波纹管固有频率相同而发生共振现象，导致波纹管发生失稳或者破坏。

2 波纹管的特征值屈曲分析

特征值屈曲分析用于预测理想状态线弹性结构的理论屈曲强度。该方法与教科书中的弹性屈曲分析一致，如立柱的特征值屈曲分析结果与经典欧拉方法一致[6]。但是，实际结构的不完美和非线性特性会导致临界载荷小于理论弹性屈曲强度，故特征值屈曲分析会导致不保守的计算结果[7]。但是对于研究屈曲载荷随波纹管的变化的规律是足够的，也是方便的。

2.1 求解结构的静力分析

使用与模态分析相同波形参数的波纹管，分别进行特征值屈曲分析，首先要对结构进行静力分析。同样先导入模型到ANSYS中，定义材料属性为304不锈钢，采用相同类型的网格划分结构，之后添加约束，将波纹管两端固定，与模态分析边界条件不同的是，在波纹管内部施加1 MPa单位载荷(图9),因为要进行屈曲分析，必须添加至少1个可以导致结构发生屈曲的结构载荷。而在波纹管膨胀节的实际工况(内压与压缩—拉伸联合作用)条件下，压缩位移仅是加速了失稳状态的出现，而内压是导致平面失稳的主要因素[8]。

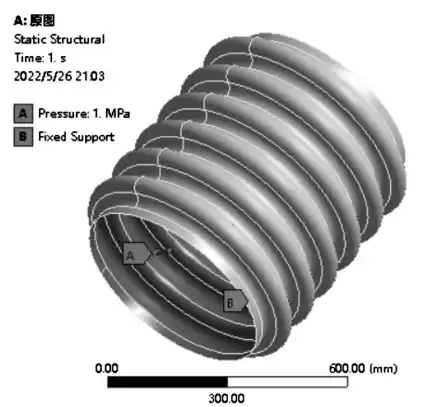
图9 波纹管的边界条件

2.2 屈曲载荷随波纹参数变化的规律

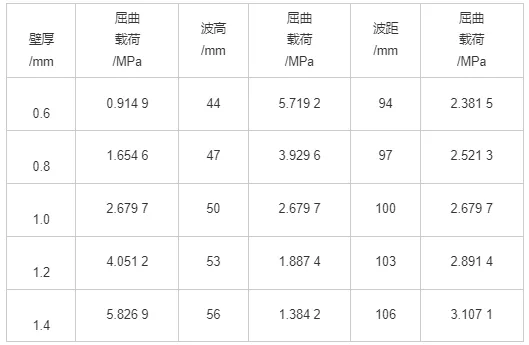
对结构进行静力分析求解后，连接Eigenvalue Buckling模块，设置特征值屈曲分支下的Analysis Settings, 在属性窗口中修改模态数进行求解，每阶模态可求解得到1个特征值，一般取第1个正数特征值定义屈曲载荷。然而当施加单位载荷时，求解得到的特征值就表示屈曲载荷，当施加非单位载荷时，求解得到的特征值乘以施加的载荷就得到屈曲载荷，特征值相当于所施加载荷的放大倍数，因此也称载荷因子。求得不同波纹参数下的屈曲载荷如表1所示。

表1 屈曲载荷与波纹参数的关系

2.2.1 壁厚

当波纹管壁厚由0.6 mm增加到1.4 mm, 对应的屈曲载荷也在不断增大，壁厚的增加可以提高波纹管的屈曲强度和平面稳定性，但是壁厚的增加会对波纹管的补偿能力造成一定的影响，疲劳寿命也会降低，给成形也带来了困难，产品造价相应提高[9]。因此，壁厚的增大或减小有利有弊，应该根据波纹管工作环境进行判断，再进行波形参数的选择，当波纹管处于内压过大，容易发生平面失稳的工作环境时，在满足波纹管补偿能力、疲劳寿命等性能的前提下，在适当的范围内可以增加壁厚，避免波纹管发生平面失稳。

2.2.2 波高

波高对屈曲载荷的影响与壁厚的影响相反，增大波高致使波纹管屈曲载荷减小，屈曲强度下降，发生平面失稳的危险性相应增加，所以为了避免波纹管平面失稳的增加，波高的尺寸设计应该小一些。而在波纹管液压成型的过程中，在模具允许的范围内，欲提高波纹管的抗压强度，采用减小波高的办法是重要的有效方法之一[10]。

2.2.3 波距

波距是影响波纹管性能的重要因素，在波纹管成形过程中，波距也是最难控制的参数[10]。当波距从94 mm增大到106 mm时，屈曲载荷从2.381 5 MPa增大到3.107 1 MPa。屈曲载荷随波距的增大而增大，波距的增大可以提高波纹管抵抗平面扭曲的能力(即平面失稳),但是增大的幅度比较小。

通过有限元分析可知，要避免波纹管发生平面失稳，可通过在适当范围内增加壁厚与波距，或减小波高的方式实现。而对不同用途或不同控制因素的波纹管，确定其波形参数应有侧重点，需综合考虑，但无论受哪种因素控制的设计，当压力较高时，都应该进行平面失稳压力的校核。

3 结论

通过建立波纹管的有限元模型，并对不同参数的波纹管进行分析可以得出以下结论：

1)利用ANSYS进行模态分析，能够求出结构的固有频率和振型，通过改变波纹参数可以改变固有频率，从而避免在工程中由于共振带来的失稳破坏，也为波纹管的设计与安装提供参考。而特征值屈曲分析是在一个理想弹性的状态下，对结构进行屈曲载荷求解，可为今后针对不完美的结构，求解极限载荷做出参考和深度计算提供依据。

2)当波纹管主要考虑平面失稳时，增加壁厚与波距，减小波高可以有效减小内压带来的平面失稳。但在实际工程中，防止波纹管发生平面失稳，需要考虑综合因素，要结合实际情况，对波纹管参数进行选择和改变，从而选择最佳方案。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删