金属丝拉拔成型技术对比：ALE与欧拉边界条件的应用

问题描述

金属丝成型的过程，可以简化为二维轴对称的模型进行计算分析（保证丝和模具的几何形状以及受力的形式均为轴对称的前提下），这可以大幅降低计算规模，提高计算效率。本次的分析分别采用了传统的拉格朗日边界模型和欧拉边界模型两种计算方式来进行对比分析，采用的计算模块均为ABAQUS/Explicit，理论上用Standard也是可以完成前者的计算的，但由于带有欧拉边界的模型只支持显式分析，所以就都采用显式进行对比，至于Standard的分析，还请有精力的坛友帮忙补完，可能的话，版主会加分的（我猜的...）。
 

有限元模型

Case 1: 拉格朗日边界的模型

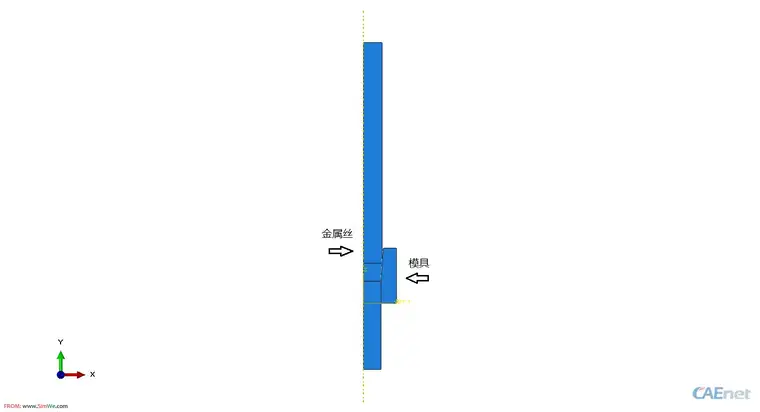
模型的建立是很简单的，如图所示，左侧较长的模型为金属丝的模型，右侧的小块体模型为模具，之所以把模具的形状建立出来而不采用解析/离散刚体来建模，这个原因后面我会解释，由于Case 1采用的拉格朗日边界， 为了达到稳定的结果，需要为金属丝建立足够长的几何形状，这样在金属丝的下端给定一个速度，则金属丝会在模具的限制下，产生塑性变形。
 

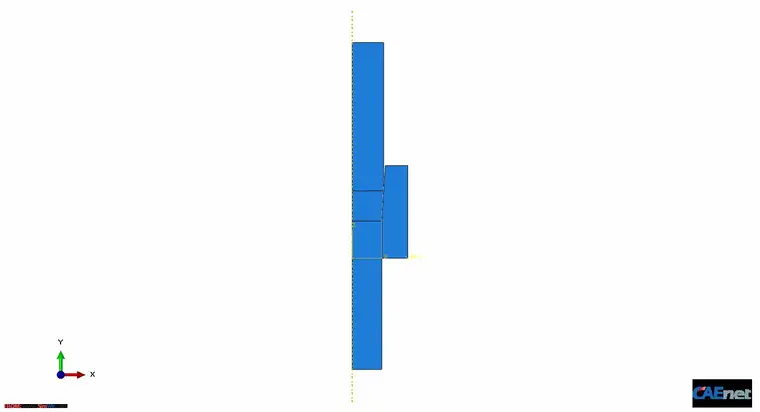
Case 2: 欧拉边界的模型

Case 2中金属丝的上下表面采用的是欧拉边界，解释一下“欧拉边界”（这个是我理解的，不对的话还请指正），其实这里我用到的关键字是 REGION TYPE=EULERIAN，准确的说是将原先的朗格朗日边界的类型人工的设定为欧拉类型， 这样的话金属丝就不用建立很长的几何尺寸，一定程度上避免了有限元模型尺寸的过大，因为在给定下端速度的欧拉边界后，金属的材料会从丝的进口端(Inflow)源源不断地“流入”，又从出口端(Outflow)源源不断地“流出”，但为了消除圣维南原理中的局部效应，金属丝的上下端均与成型区保持有足够的距离。
 

材料属性  
为了有对比性，两个Case的材料属性均一致，其中：金属丝的弹性模量为38GPa，初始屈服应力为27MPa，泊松比为0.33，密度是2672 kg/m^3.
 

边界条件
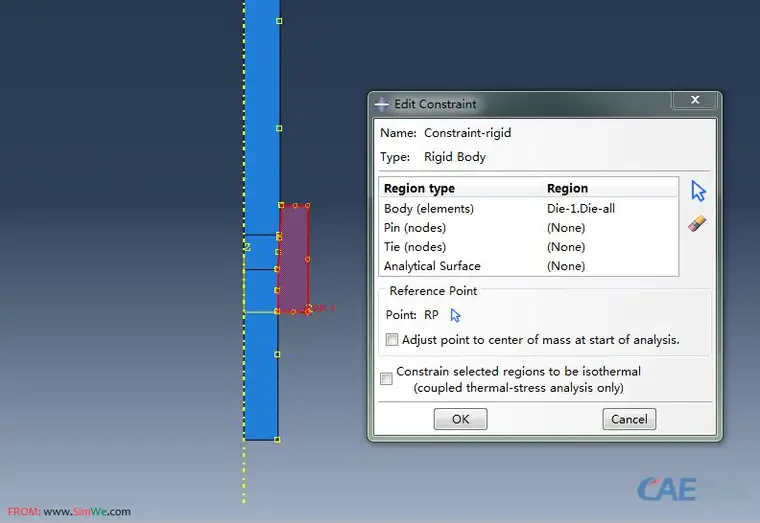
Case 1：为模具施加了Rigid body约束，把模具强制为刚体，并给出刚体参考点，如图所示；

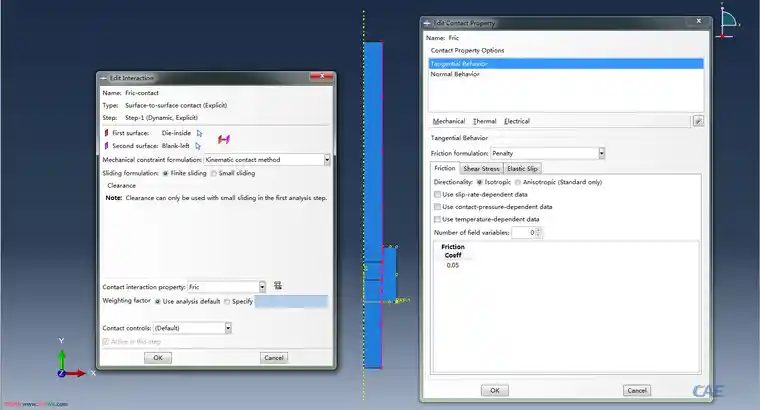
模具与金属丝之间建立Surface-Surface接触条件，并给定摩擦系数0.05，其中，法向的接触属性给定的是“硬接触（Hard Contact）”，如图所示：

为刚体参考点施加固支约束，如图所示：

为金属丝的下表面施加速度边界（Velocity），其中，速度施加的幅值曲线采用的是Smooth形式加载，以模拟准静态过程，如图所示：

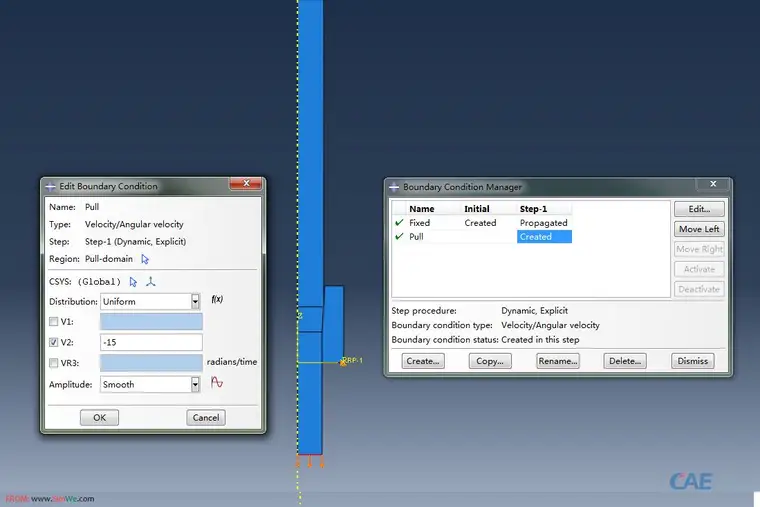
Case 2：边界条件与Case 1基本相同，所不用的是Cace 2中，为金属丝的上下表面都设定了欧拉类型的边界，同时，为了防止网格畸变过大，必须在Step模块为金属丝设定ALE参数，详细的操作在下一节有描述。
 

建模要点

“别人无法重复其结果”——这句话应该是讥讽的意味吧，所以本帖子中给出建模过程中的几个要点以及需要注意的地方，以方便读者重复。
 
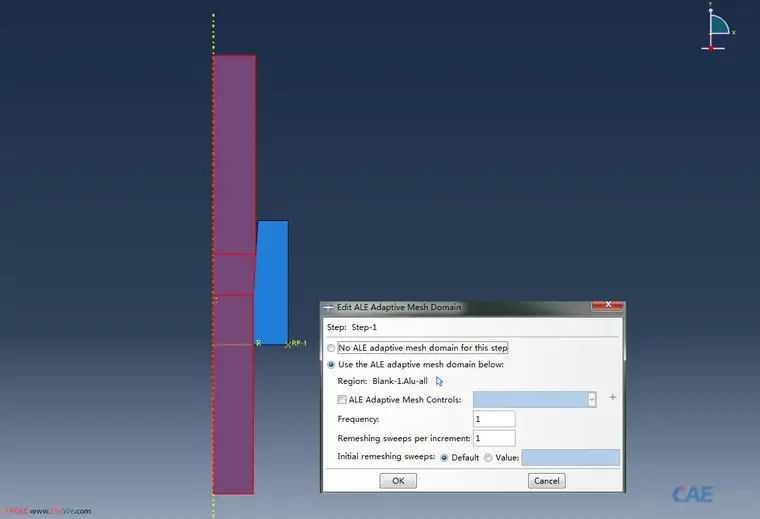
1）Case 2中，在Step模块下，需要为金属丝的模型设定ALE参数，其中，频率需要设定为1（ 维持缺省设置也是可以的，不过用CAE提交Job时会报错，解决方法：采用Command提交即可），如图所示：

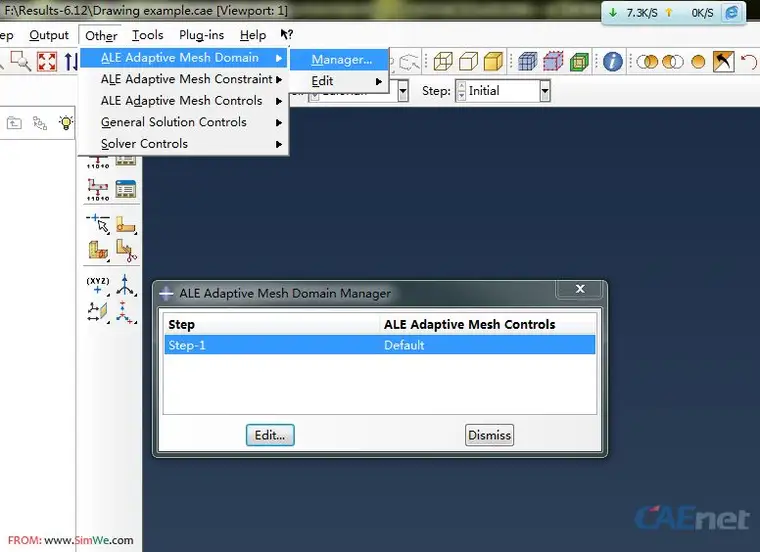
2）设定好ALE参数后，还要为金属丝的上下表面给定ALE自适应网格约束，目的是约束自适应的网格几何边界，避免计算过程中几何边界的突然“跳动”，如图所示：

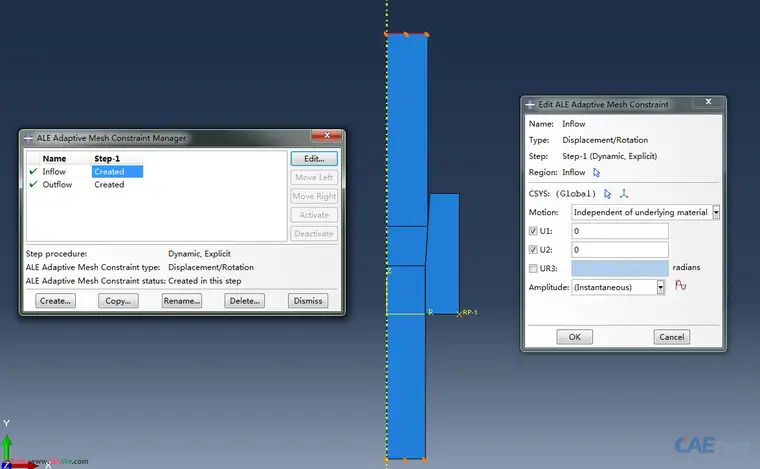
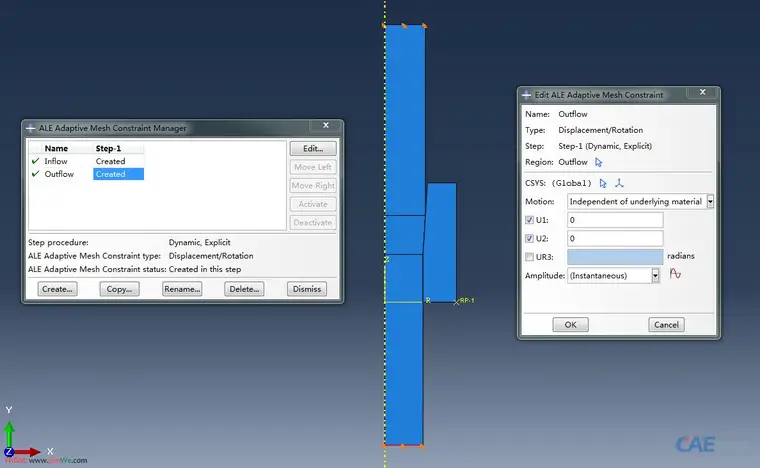
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删