铆钉成型模拟在Abaqus中的实现

Abaqus Document帮助文档的2.3.1 节Rivet forming介绍铆钉成型模拟过程，有两种方法，纯拉格朗日法（pure Lagrangian）与CEL方法（coupled Eulerian-Lagrangian），拉格朗日方法的缺陷在于无法解决大变形问题，但是可以利用ALE技术（网格重划分），CEL方法可以很好地解决大变形问题，网格不动，材料在网格中移动。

Part，Property，Assembly，Mesh模块的建模过程省略，帮助文档提供了inp文件。

拉格朗日方法：

   拉格朗日方法的有限元模型
 

Step模块：

Explicit显示动力学分析步，分析时间为0.001s，场变量与历史输出变量为帮助文档默认。

   动力学分析步
 

Interaction模块：

通用接触的设置默认，接触属性为法向硬接触（Hard Contact），切向无摩擦（Frictionless）。也可以用面对面接触（Surface to Surface Contact），需要分别建立两个dies，plate与工件的接触。定义两个dies与plate为刚体。

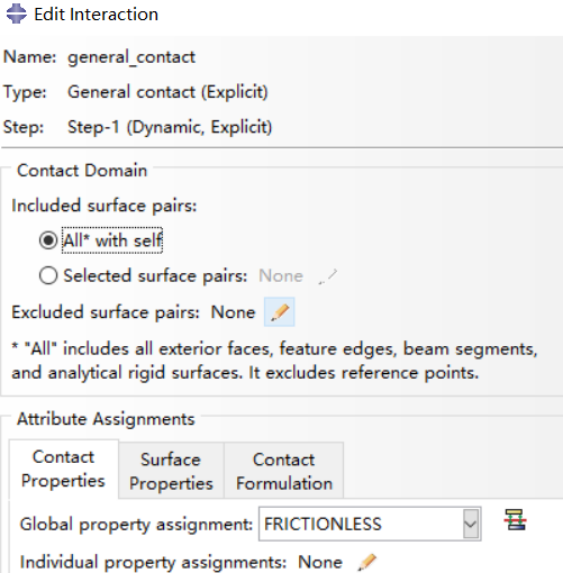
   通用接触设置
 

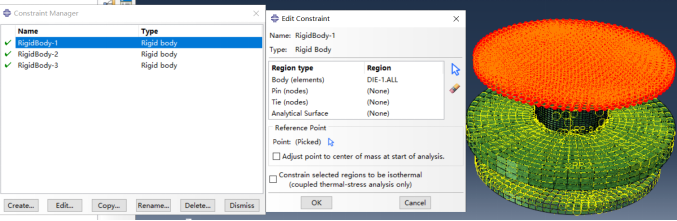
   定义刚体
 

Load模块：

上模向下移动3mm，下模向上移动2mm，中间的plate约束6个自由度。

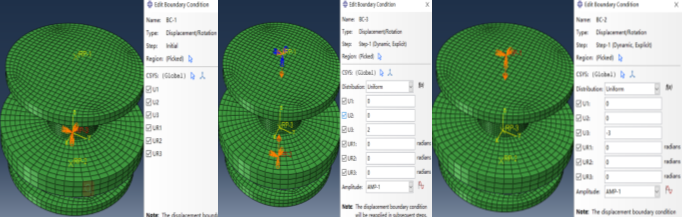
   载荷工况
 

Mesh模块：

C3D8R缩减积分单元，网格参数设置为软件默认。

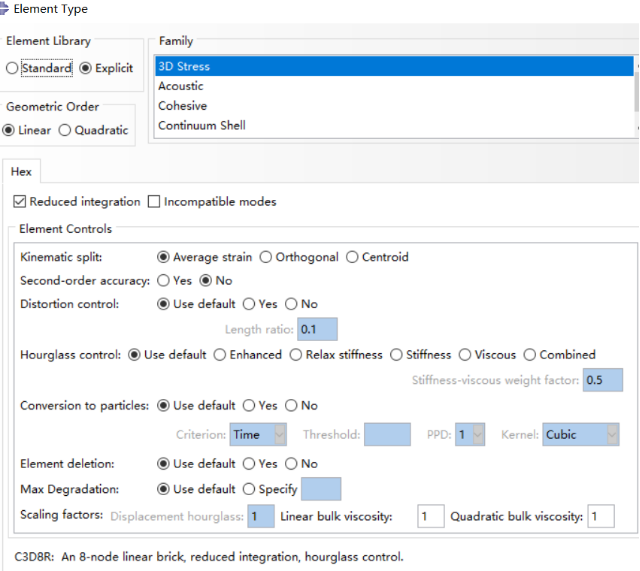
   缩减积分单元
 

CEL方法：

CEL方法与拉格朗日方法在建模上有明显的不同，铆钉为欧拉体，建模时欧拉体的体积要大于铆钉的体积，然后从欧拉体中切分出铆钉的形状，如下图。

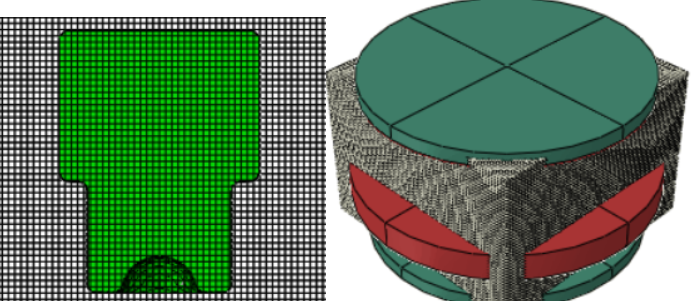
   CEL方法的有限元模型
 

分欧拉网格时要利用体积分数工具命令（工具栏，Discrete Filed，Volume Fracton Tool），先选择欧拉体，再选择铆钉模型（在菜单栏的Assembly中要将铆钉零件抑制掉）。但是CEL方法只能用通用接触。

Mesh模块：

   欧拉网格设置
 

后处理模块：

拉格朗日网格的扭曲比较严重，而且网格有明显的穿透现象。

   拉格朗日网格
 

CEL方法适合解决大变形问题，但是也有轻微穿透现象，网格密度越大，计算的结果越精确，但是CEL方法的计算时间很长，而且不能使用质量缩放。

   欧拉网格
 

总结：

CEL方法不仅可以应用于CEL分析，还可以用于解决大变形问题。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删