产品
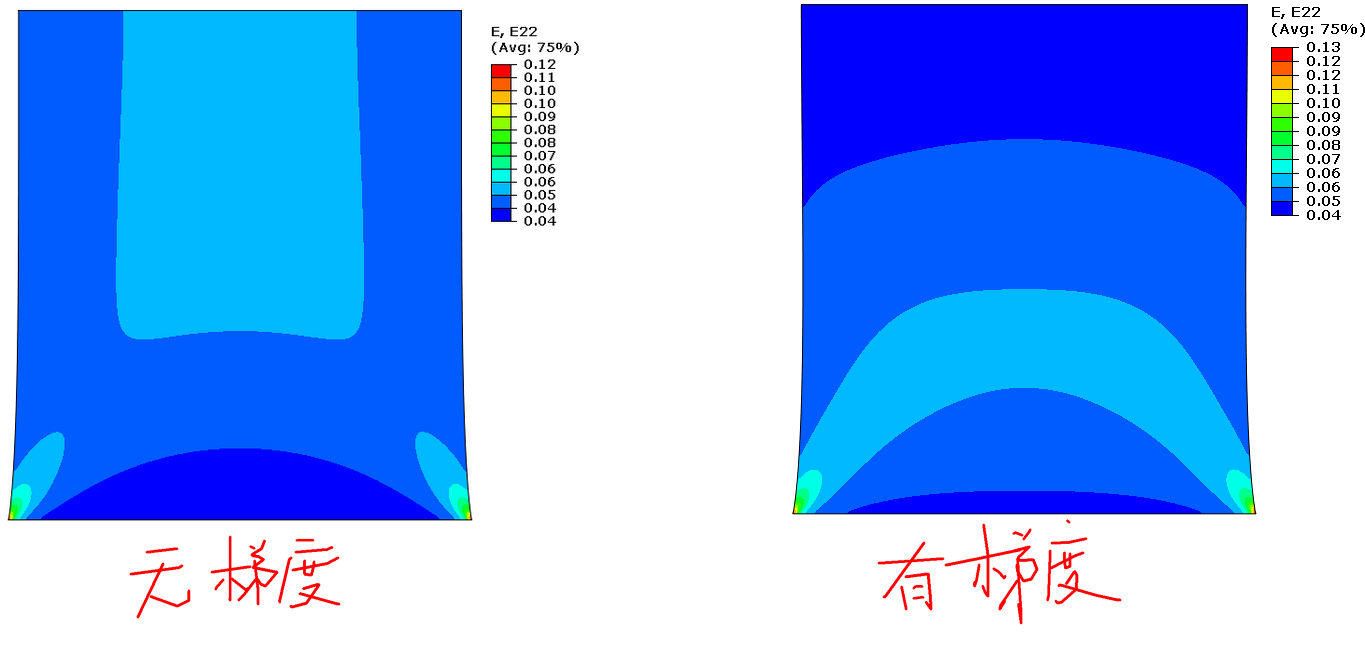
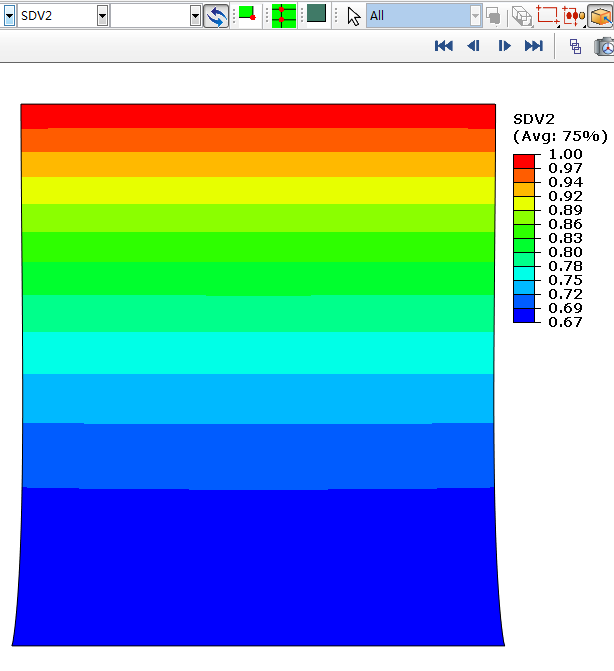
模量随y坐标变化的模型的状态变量
无梯度代表着均匀模量模型，有梯度代表模量从下到上随y坐标变化（如果想让它随x坐标也变化，可以修改程序，很简单）
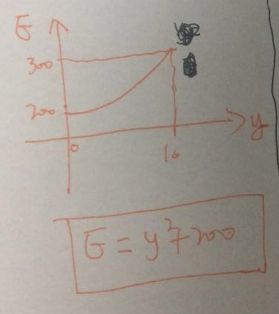
模量随y坐标成抛物线变化，底端固定，上面施加拉伸载荷
结果分析：
1 状态变量值的大小代表了模量的大小（程序中设置E与状态变量是线性关系），从状态变量的云图结果可以看出，底端模量最小，SDV2值最小，随着y增加，开始增加很慢，然后增加速率增大，顶端的SDV2值最大，由此可知，模量随y抛物线变化程序是没有问题的；
2 从y反向的弹性应变也可以看出：对于均匀的弹性模量模型，因为总体模量都是200GPa，所以相同的拉伸载荷之后，y方向的弹性应变更大，这也印证了程序的正确性；
以下打包文件中包含源程序和例子：
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
