基于Vumat子程序的Lemaitre损伤模型应用

随着理论研究与计算手段的不断发展，为了得到更加准确、更加可应用于工程的计算结果，人们已不再简单地满足于各类基础的理想模型。例如，许多基于断裂力学的弹塑性材料的失效准则常表征为一个应力和塑性应变的方程，但这些失效模型往往与其塑性演化规律不耦合，计算结果也与实际存在着一定差距。于是，Lemaitre等人又基于连续损伤力学，在本构模型中考虑了材料退化和损伤演化状态变量，提出了Lemaitre损伤模型，为弹塑性材料的断裂分析提供了一种从裂纹产生、扩展直至最终破坏的较为系统的方法。

本期，我们就讲讲如何在ABAQUS中基于Vumat子程序来实现在Mises塑性材料中引入Lemaitre损伤规律，以较为准确地模拟材料的损伤演化过程。

1. 方法概述—“算法分裂”

顾名思义，弹塑性材料在变形过程中既有弹性阶段，也有塑性阶段。因此，损伤模型在也把问题分为了弹性部分和塑性部分，即所谓的“算法分裂”。具体思路如下：

1.首先，建立材料的本构。根据Mises屈服准则的相关理论，在Vumat中建立材料本构方程，并在其中引入Lemaitre损伤规律，Lemaitre损伤规律如下所示：

2.然后，进行弹性预测。在这一步中，我们要假设应变是完全弹性的。同时，利用ABAQUS显式运算的方法，用在屈服面内的t_i时刻的弹性预测状态变量计算t_i+1时刻的对应变量，直至材料进入塑性阶段。

3.最后，进行塑性变形分析。当材料进入塑性变形阶段后，在子程序中实现每一个时间增量步下，各类参数（如应力、应变、Lemaitre损伤变量等）的不断更新。

2. 案例

本文以铜板的无压头穿孔为例，利用Vumat子程序预测了它的破坏载荷。

2.1 问题描述

无压头穿孔是一种用高压流体代替普通压头进行穿孔的工艺，如图1所示，工件被放置在模具中夹紧，高压流体通过模孔对工件进行穿孔。本文所用案例的具体尺寸及细节部分网格如图2所示（取一半的模型）。工件采用了99.9%的铜。

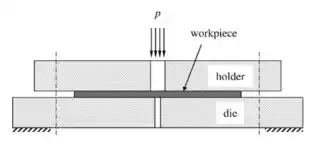
图1 无压头穿孔工艺示意图

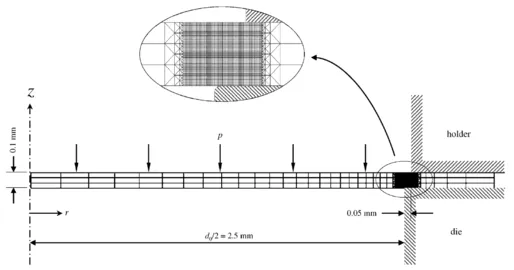
图2 无压头穿孔有限元模型（一半的模型）

2.2 结果展示

依据以上方法，计算得到当压力值为12.35MPa时，铜板发生了断裂破坏，相较于文献^[1]中所给的14.7MPa的试验数据小了约16%，其原因可能有以下几点：

1.  案例中所使用的材料参数为从另一文献中所得，可能与试验所用材料存在略微的差别。

2.  在仿真时简化模型，使得边界过于理想化。

裂纹的产生和扩展图如图3所示，可看出当载荷达到12.34MPa时，在板材的上表面和模具拐角出现了初始裂纹。当载荷达到12.35MPa时，板材发生了破坏。计算所得的断裂剖面也与试验相似，进一步说明了这一算法的准确性。

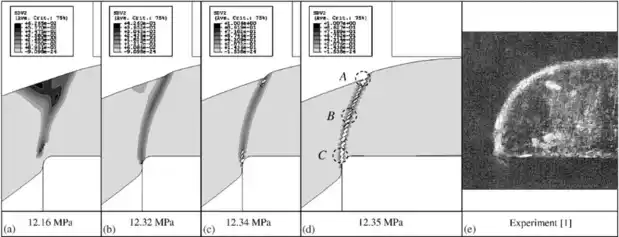
图3 裂纹扩展及试验断裂剖面图

提取下模沿Z方向的力，可得到图4。从图中可看出，初始阶段下模压力由于摩擦原因快速增加，当裂纹刚开始出现时，下模压力增加到了最大，而当材料断裂后，该力突然下降到0。这也显示了无压头穿孔与传统的压头穿孔工艺有着较大的区别。

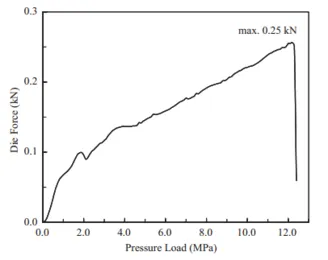
图4 下模压力随载荷变化曲线

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删