看了Usim大佬的水滴的欧拉分析,十分感兴趣。前往帮助文档一查,正好有介绍和算例。本文就照着做一遍,查查文档学习一下欧拉分析。本例利用欧拉方法模拟液体在重力作用下的大变形动态坍塌过程。
二维近似
1.建模
直接利用10×5×0.05m的长方体来建立欧拉域。由于欧拉分析只能在三维空间中执行,所以通常用厚度方向一个单元的三维实体模型来近似二维问题。为了方便选取参考体(Reference instance),对欧拉零件进行了切分。注意,建立part时要保证5m的高度方向是在Z方向(与后面加载初始应力有关)。


2.材料
水可视为近似不可压缩、粘性的牛顿流体,模型中采用了Mie-Gruneisen状态方程的线性Us-Up Hugoniot形式,相关材料参数如下

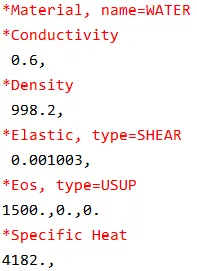
注意,表格中的参数与inp文件中的参数略有不同。表格中为粘度Viscosity(Pa·s),而inp文件中为剪切模量(Pa),单位也不一致,以表格为准。
3.网格
在欧拉分析中,均匀的立方体单元能够给出比较好的计算结果。因此统一单元尺寸在0.05,即厚度方向一个单元。
4.载荷
1)初始的材料赋予(material assignment)
在欧拉分析或CEL分析中,最重要的一步即为欧拉域中的参考体赋予材料,通常有两种方式。
Uniform definition:一种是针对比较简单能够通过分割欧拉实体得到目标材料区域,之后在load模块的预定义场中,双击Region选择将要赋予材料的区域,将对应材料实例的体积分数设为1,表明该区域的每个单元都填满该材料(图中的material-water-1),空域(Void)体积分数设为0,这样就将所选择的区域填充满指定材料,即实现了材料在欧拉域中的几何分布。
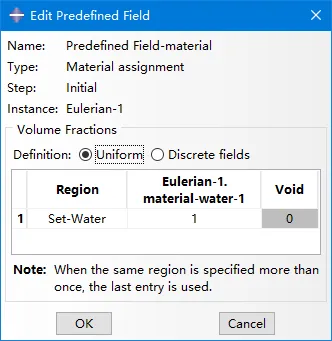
延伸
一般来说,欧拉属性(section)可以包含多种材料,相应地有多个材料实例(material instance),因此在预定义场赋予材料中也有相应的体积分数指定,如下图
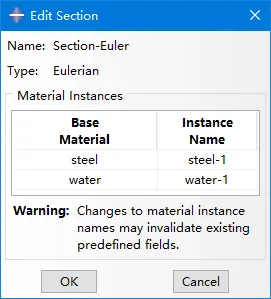

图中的参数表示所选区域内的所有单元的组分都为:50%的水和50%的钢(Uniform的含义),对于这种情况abaqus是无法分析出具体的几何组成,即无法判断各种材料的边界,预计无法计算。因此采用Uniform方式给欧拉零件部分区域赋予材料实例一般要求:
①欧拉零件几何简单,能够通过分割得到目标区域,且不会造成网格质量太低的问题;
②如有不同的材料需要在预定义场中赋予,则首先需要分割欧拉零件,保证每个区域填满一种材料。
2)初始的静水压力
初始状态下,水柱内部还存在自重带来的静水压力,需要利用geostatic stress实现。该自重应力由自身重力引起,因此随深度呈线性变化p=ρgh,需要两个点坐标来定义,即(幅值1,深度1)和(幅值2,深度2)。注意,在三维模型和轴对称模型中,该自重应力的竖直方向(即深度方向)为Z方向,在二维模型中,竖直方向为Y方向。横向系数1和2分别定义了X方向和Y方向的应力系数。

3)重力:Z方向(-9.81m/s2)
4)边界
欧拉域的所有边界面上施加速度为零的边界条件,以防止材料流进或流出欧拉域。
三维模型
1.建模
该问题也可建立1/4的三维模型来求解,采用对称边界。需要建立两个零件:欧拉域(欧拉零件)为10×10×5m的长方体,变形体(参考零件)为1/4圆柱,半径2.25m,高度4.5m。如果继续用上面的直接分割欧拉零件得到变形参考体,则欧拉网格的质量不会太好,影响计算的准确性。而且为了生成较为准确精细的离散场,这里对欧拉零件也进行了分割。

2.网格
其他步骤与上面的近似二维模型类似,为比较结果,欧拉网格尺寸应设置为0.05,但网格太密,计算时间较长。因此网格尺寸设为0.125。
3.载荷
1)材料赋予
与前述近似二维模型不同的是三维模型采用离散场赋予材料属性。首先通过Tool-Discret-VFT工具将欧拉网格内的参考体所占据的空间生成离散场DiscField-Water,再将材料赋予给离散场,Region选择整个欧拉实例,这样离散场构成的区域就是材料填充的区域,以此来定义变形体的初始空间几何。
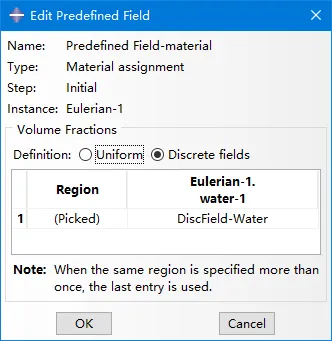
拓展
通过离散场赋予初始材料的方式比较灵活,单个欧拉单元中可以包含多种材料。相比于Uniform定义,离散场方式除了欧拉实例(已划分网格)以外,至少还需要一个参考实例。其实,通过VFT工具得到的离散场其实是参考实例占据欧拉网格所形成的单元体积分数阵列,指定给每个单元的component就是参考体在该单元中的体积占比,可参考Abaqus/CAE User's Guide (6.14) (wufengyun.com) 。

这里假设两个材料(水和钢材),所以定义了两个离散场,分别赋予水和钢材。如上图,左下的灰色参考体占据4号单元体积的0.06118,右中的红色参考体占据1和2号单元各0.06118(注意下图中的Field ),没有涉及的单元默认值都为零,即空材料。

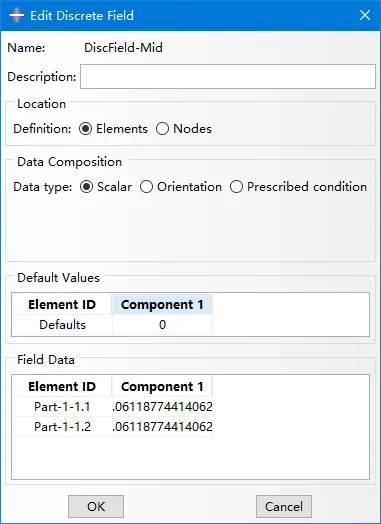
如下图预定义场,Region双击选择欧拉实例,钢材填充下部的离散场DiscField-Bot,即占据4号单元的0.06118;水填充中部的离散场DiscField-Mid,即占据1号和2号单元各0.06118,这就实现了材料部分占据单元。从上面离散场编辑对话框看出,理论上甚至可以手动添加或修改单元和对应的材料体积分数。

2)边界
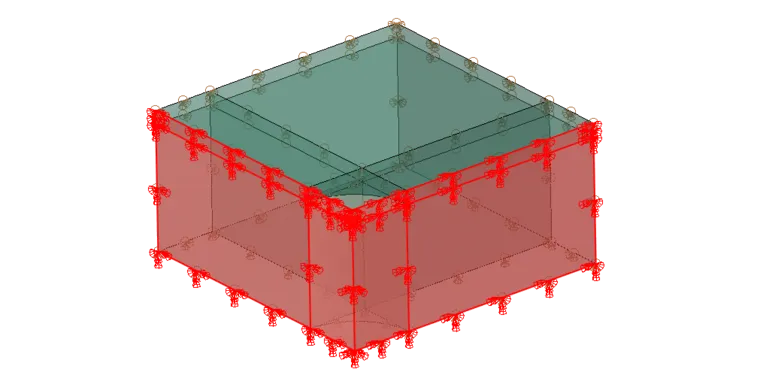
在欧拉零件对称面上对称边界,其他面还是速度为零约束。
结果讨论
2D vs 3D:左侧三维轴对称模型,右侧近似二维模型(水平速度云图)

t=0s

t=0.5s

t=1.0s
显然三维轴对称模型在速度上更小一些,而且可以绘制如下的水浪的前端的位置-时间曲线。
曲线的实现方式:将模型底部的一“条”单元单独显示出来(最好前处理定义单元集),然后提取该单元集在积分点处的含水体积分数随时间变化曲线,求和,将纵坐标乘以单元长度(近似二维0.05,三维0.125),便可得到距离-时间曲线。

下图为帮助文档中结果,图中abaqus结果为近似二维模型结果,点线为试验结果(1s时刻8.2m)。

可以发现近似二维模型偏高(1s时刻9m),三维轴对称模型偏低,1s时刻7.5m(如果加密效果可能会更好)。
疑问:试着去掉了初始自重应力geostatic stress,结果(右侧无geostatic stress)如下

t=0.5s

t=1.0s
可以发现结果几乎没有变化,为什么?是影响太小可以忽略还是问题本身就不需要这个自重应力?
个人觉得不需要,如果水柱周围包裹着圆柱,则在重力作用下以及圆柱的约束,自然存在静水压力;一旦撤走包裹的圆柱面,侧向压力瞬间消失,但这个水柱形体瞬间不会改变,只有重力作用。类似一个装满水的气球,突然将气球扎破,水基本还是球体形状,之后再重力作用下发生变形。不知道理解的对不对,流体基本上都忘了。有兴趣的有能力的可以做一下刺破装满水的气球的案例,看看效果,期待高手大佬们发帖!!
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删