探究Abaqus/Explicit显示分析中速度定义的多样性与结果比对

密度，弹性模量，泊松比

速度的不同定义方式可以类比直接耦合的温度场的定义；

interaction模块的接触十分重要（通常是选择通用接触all* with self，也或者用面面接触）；

预定义场定义的速度是初始速度，只在初始时刻起作用，后续的任何时刻的速度软件自己计算得到的，这也是为什么预定义初始速度场后，在后续的分析步都显示的是computed；

如果同时设置预定义初始速度场和BC的初始分析步速度0，那么预定义初始速度场将被BC的初始分析步速度0覆盖，因此，模型的初始速度为0；

1 自由落体运动

只施加重力加速度即可，初始速度为0，因此没必要用预定义场定义初始速度

分析步时间：接触地面时候的时间可以估算出来：h=(1/2)*g*t^2；

接触地面时的速度为v=g*t；

2 匀速运动

使用预定义场定义一个初始速度，预定义场速度只在初始时刻起作用；

如果考虑重力问题就加上，下落过程中，速度不断增大，反弹之后的速度在重力作用下不断减小，然后再下降撞击板，再反弹，...

如果不考虑就不加，类似于在真空中，反弹后也保持匀速（由于接触时能量消耗转变为了材料变形，反弹后的速度小于预定义场速度）

3 带加速度的运动

需要使用预定义速度场定义一个初始速度，再利用BC中的加速度定义一个某个方向的加速度，可以得到某时刻的瞬时速度：Vt=V0+at, s=V0*t+(1/2)a*t^2或者Vt^2-V0^2=2as；

4 使用BC里的速度来直接定义一个速度

需要使用预定义场定义一个初始速度，然后利用BC在分析步中定义一个速度值，速度加载方式默认为instantaneous，也就是说在初始瞬时就达到了这个速度，之后保持不变；如果定义了幅值曲线，那么速度的变化将按照幅值曲线变化。

一个简单的例子结果对比：

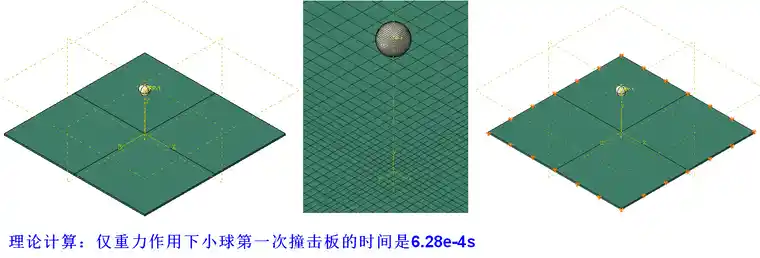
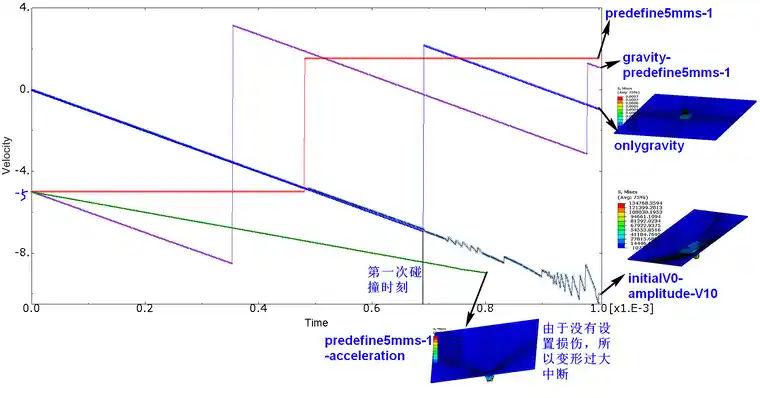
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删