直接根据牵引-分离定律定义的粘聚行为:
可用于直接根据牵引力与分离模拟复合材料界面的分层;
允许指定材料数据,例如断裂能作为界面处法向与剪切变形(模式混合)之比的函数;
假设损伤前为线弹性牵引分离规律;
可以与Abaqus/Explicit中的线性粘弹性结合使用来描述率相关的分层行为;
假设单元的破坏以材料刚度的逐步退化为特征,这种退化是由损伤过程驱动的;
允许多种损伤机制;
可以与Abaqus/Standard中的用户子程序UMAT或Abaqus/Explicit中的VUMAT一起使用,以指定用户自定义的牵引分离定律。
1. 使用牵引-分离定律定义本构响应
为了直接根据牵引和分离来定义粘聚力单元的本构响应,在定义粘聚力单元的截面行为时选择牵引-分离响应。
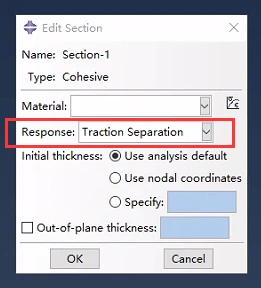
CAE定义
2. 线弹性的牵引-分离行为
Abaqus中现有的牵引-分离模型假定初始为线弹性行为,随后为损伤的起始和演化。弹性行为用弹性本构矩阵表示,该矩阵将界面上的名义应力与名义应变联系起来。名义应力是力分量除以每个积分点的原始面积,而名义应变是每个积分点的分离量除以原始厚度。如果指定牵引-分离响应,则初始本构厚度的默认值为1.0,以确保名义应变等于分离量(即上下面的相对位移)。用于牵引分离响应的本构厚度通常不同于几何厚度(几何厚度通常接近或等于零)。
名义牵引应力矢量 t 由三个分量(二维问题中的两个分量) tn、ts 和 (三维问题中的) tt组成,分别表示法向(三维情况下沿局部3方向和二维情况下沿局部2方向)和两个切向(三维情况下沿局部1和2方向以及二维情况下沿局部1方向)的牵引力。相应的分离量用δn、δs和δt表示。用粘聚力单元的原始厚度T0表示,名义应变可定义为:
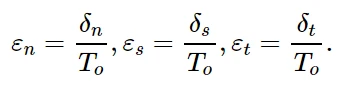
名义应变=分离量/初始厚度
弹性行为可以写成:
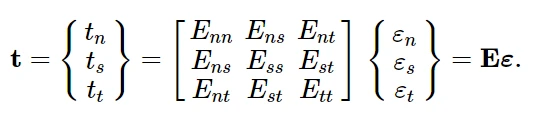
弹性矩阵在牵引向量和分离向量的所有分量之间提供了完全耦合的行为,并且可以依赖于温度和/或场变量。如果期望法向和剪切分量之间的非耦合行为,则将弹性矩阵中的非对角线项设置为零。
可选地,对于非耦合牵引行为,可以指定压缩因子,这确保了压缩刚度等于指定的因子乘以拉伸刚度,Enn。该因子仅影响在法向分离时的牵引响应,剪切性能不受影响。
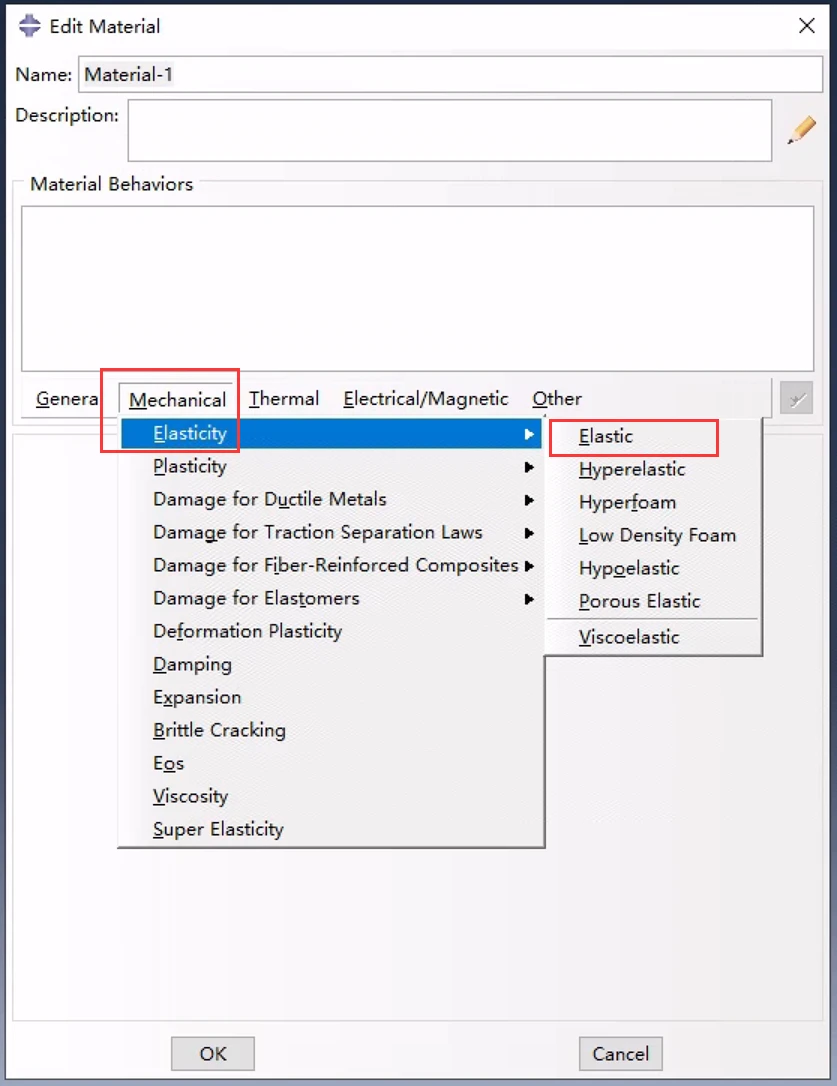
定义线弹性材料行为
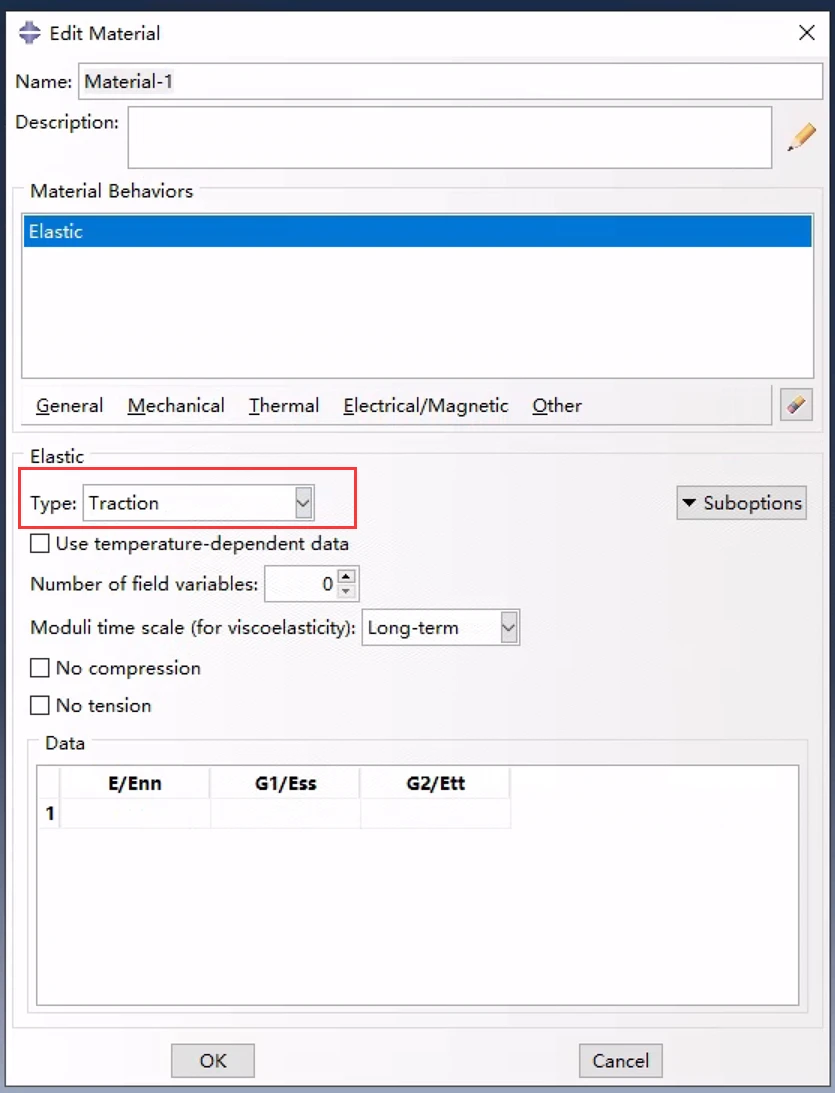
定义非耦合的牵引分离行为
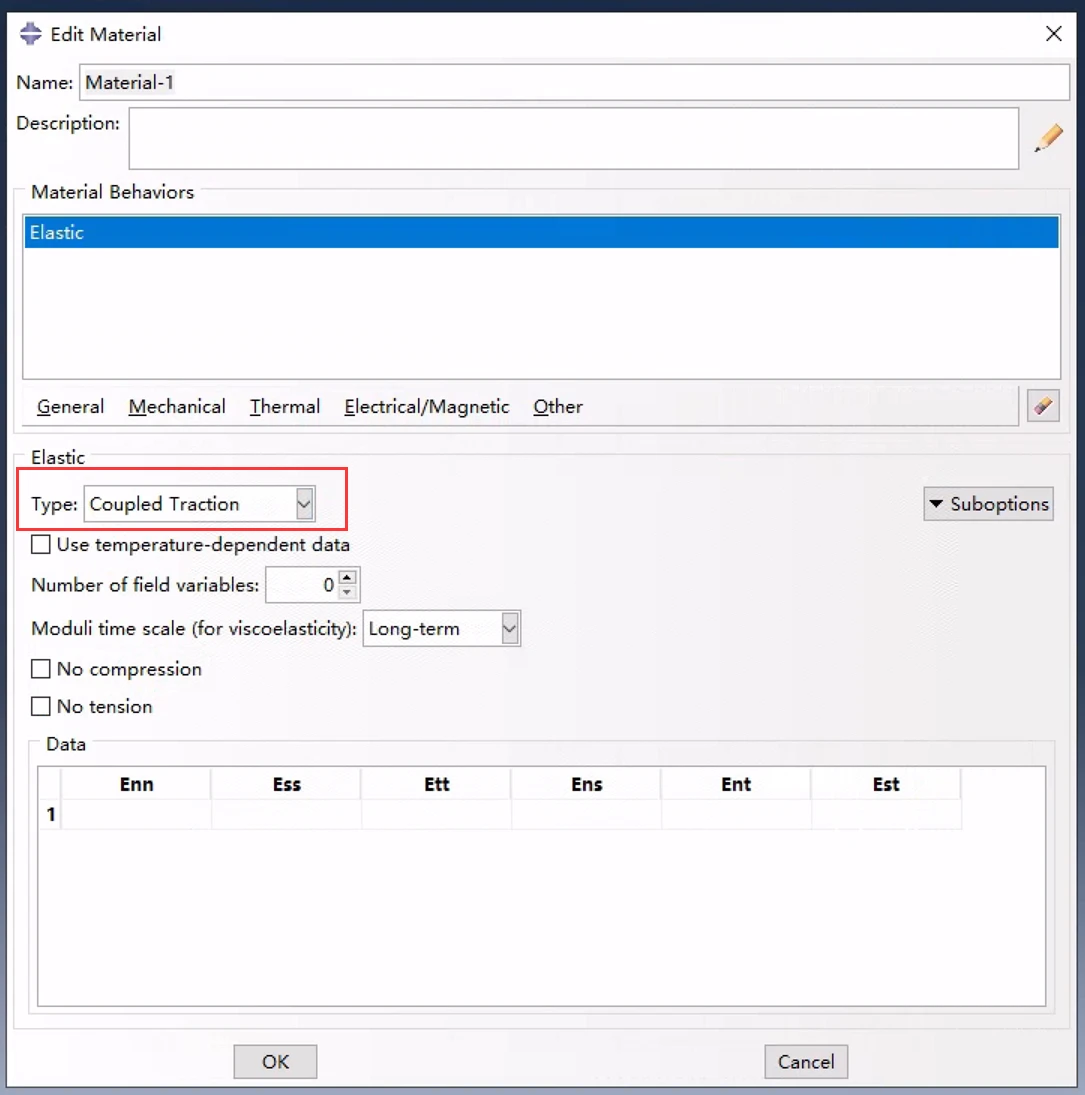
定义耦合的牵引分离行为
另外,在Abaqus/CAE中不支持为非耦合的牵引分离行为指定压缩因子,使用输入文件指定:

输入文件的定义
3. 材料属性解释
通过研究长度为L、弹性刚度为E、原始面积为A的桁架在轴向载荷P作用下的位移方程,可以更好地理解牵引-分离模型的界面弹性刚度等材料参数:
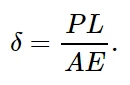
加载下分离(位移)的计算
这个方程可以写成:
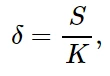
其中S = P / A为名义应力,K = E / L是将名义应力与位移联系起来的刚度。同样,假设密度ρ,桁架的总质量为:
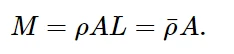
由上式可知,如果对刚度和密度进行适当的重新解释,可以将实际长度L替换为1.0(以保证应变与位移相同)。特别是,刚度为K = (E / L),密度为¯ρ = (ρ L),其中桁架的真实长度用于这些方程中。密度表示单位面积的质量,而不是单位体积的质量。
这些想法可以延续到粘聚层的初始厚度Tc。如果粘接材料具有刚度Ea和密度ρc,则界面的刚度由Ec = (Ea / Tc) To给出,界面的密度由¯ρc = (ρc Tc)给出。如前所述,无论粘聚层的实际厚度如何,牵引与分离响应建模的本构厚度To的默认是1.0。在这种情况下,名义应变等于相应的分离。当粘聚层的本构厚度“人为”设置为1.0时,理想情况下,应该将Ec和¯ρ c(如果需要)分别作为材料刚度和密度,并根据粘聚层的真实厚度计算。
上述公式提供了一种方法,用于根据块状胶粘剂材料的材料特性估计牵引分离行为界面进行建模所需的参数。
当界面层厚度趋于零时,上述方程意味着刚度Ec趋于无穷,而密度¯ρc趋于零。这种刚度通常被选为罚参数(penalty parameter)。过大的罚刚度不利于Abaqus/Explicit中的稳定时间增量,并可能导致Abaqus/Standard中的单元运算符条件不良。
4. 在Abaqus/Explicit中建立率相关的牵引分离行为
时域粘弹性可以在Abaqus/Explicit中对具有牵引-分离弹性的粘聚力单元的率依赖行为进行建模。法向和两个剪切名义牵引力的演化方程为:
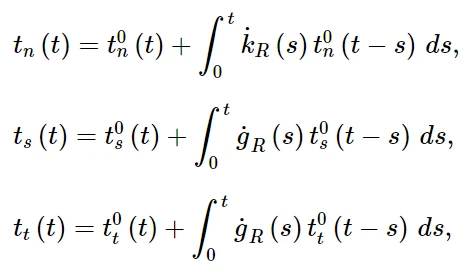
其中t0n (t)、t0s (t)和t0t (t)分别为t时刻在法向和两个局部剪切方向上的瞬时名义牵引力
函数g R (t)和k R (t)分别表示无量纲剪切模量和法向松弛模量。
对于非耦合牵引弹性,假定粘弹性法向和剪切行为是独立的。法向松弛模量定义为:
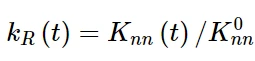
其中K 0 nn是瞬时法向模量
假设剪切松弛模量是各向同性的,因此与局部剪切方向无关:
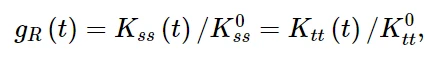
其中k 0 s s和k 0 t t是瞬时剪切模量
对于耦合的牵引-分离弹性,法向和剪切松弛模量必须相同,g R (t) = k R (t),并且必须使用相同的松弛数据。
最后,还可以将时域粘弹性与渐进损伤和失效模型结合起来。这种组合允许在初始弹性响应期间(在损伤开始之前)以及在损伤演化期间模拟率相关的行为。
以上是牵引分离方法建立粘聚力单元的材料和截面的定义方法;下面将继续牵引分离方法建立粘聚力单元的损伤相关。
5. 损伤建模
Abaqus/Standard和Abaqus/Explicit都允许对粘聚层的渐进损伤和失效进行建模,且其响应是根据牵引-分离来定义的。相比之下,只有Abaqus/Explicit允许用传统材料建模的粘聚力单元的渐进损伤和破坏建模。牵引-分离响应的损伤是在与常规材料相同的一般框架内定义的。这种总体框架允许同时作用于同一材料的几种损伤机制的组合。每一种损伤机制都包含三个要素:损伤起始准则、损伤演化规律以及在达到完全损伤状态时移除(或删除)单元的选择。虽然牵引-分离响应和传统材料的一般框架是相同的,但如何定义各种成分的许多细节是不同的。因此,牵引-分离响应损伤建模的细节如下。
如上所述,假定粘聚力单元的初始响应是线性的。然而,一旦满足损伤起始准则,材料就会按照自定义的损伤演化规律发生损伤。图1显示了具有损伤机制的典型牵引分离响应。如果没有相应的损伤演化模型,则Abaqus将仅为输出目的对损伤起裂准则进行评估;对粘聚力单元的响应没有影响(即不会发生损伤)。黏结层在纯压缩下不发生损伤。
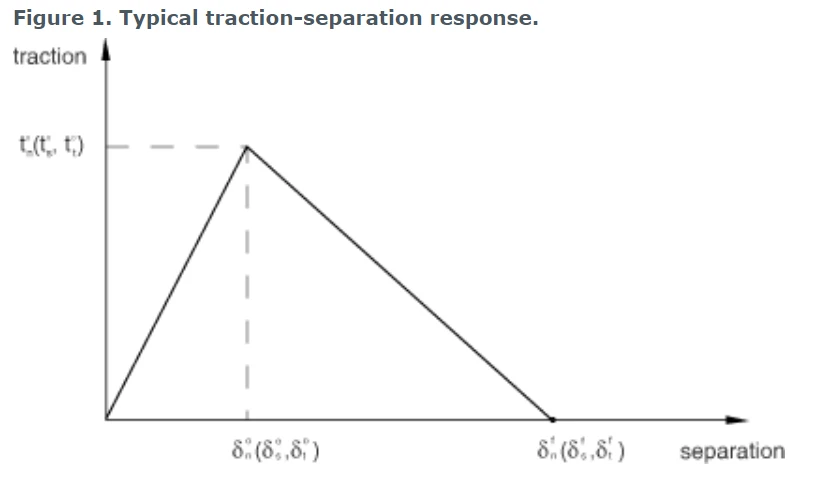
图1 典型的牵引-分离响应
6. 损伤起始准则
顾名思义,损伤起始是指某一材料点的响应退化的开始。当应力和/或应变满足指定的某些损伤起始标准时,退化过程开始。每个损伤起始准则有一个与之相关联的输出变量,以指示是否满足该准则。1或更大的值表示满足起始化条件。没有相关演化规律的损伤起始准则只影响输出。因此,可以使用这些标准来评估材料遭受损伤的倾向,而无需实际模拟损伤过程(即,无需实际指定损伤演变)。
在下面的讨论中,t o n、t o s和t o t分别表示变形完全垂直于界面或完全在第一或第二剪切方向上时的名义应力峰值。类似的,ε on、ε o s和ε o t分别表示变形完全垂直于界面或完全在第一或第二剪切方向上时的名义应变峰值。当初始本构厚度To = 1时,名义应变分量等于粘聚层顶面和底面之间的相对位移δ n、δ s和δ t。在下面的讨论中使用的符号⟨⟩表示麦考利Macaulay括号。麦考利括号用于表示纯压缩变形或应力状态不会引起损伤。
6.1 最大名义应力准则
当最大名义应力比(定义见下式)达到1时,假定损伤开始。这个标准可以表示为:
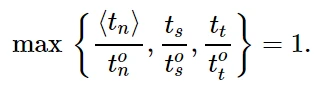
最大名义应力准则
CAE中的定义位置
6.2 最大名义应变准则
当最大名义应变比(定义见下式)达到1时,假定损伤开始。这个标准可以表示为:
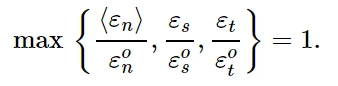
最大名义应变准则

CAE中的定义
6.3 二次名义应力准则
当名义应力比(定义见下式)的二次相互作用函数达到1时,假定破坏开始。这个标准可以表示为:

二次名义应力准则
CAE中的定义
6.4 二次名义应变准则
当名义应变比(定义见下式)的二次相互作用函数达到1时,假定损伤开始。这个标准可以表示为:
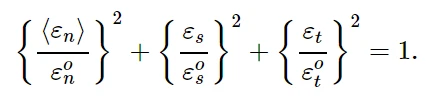
CAE中的定义
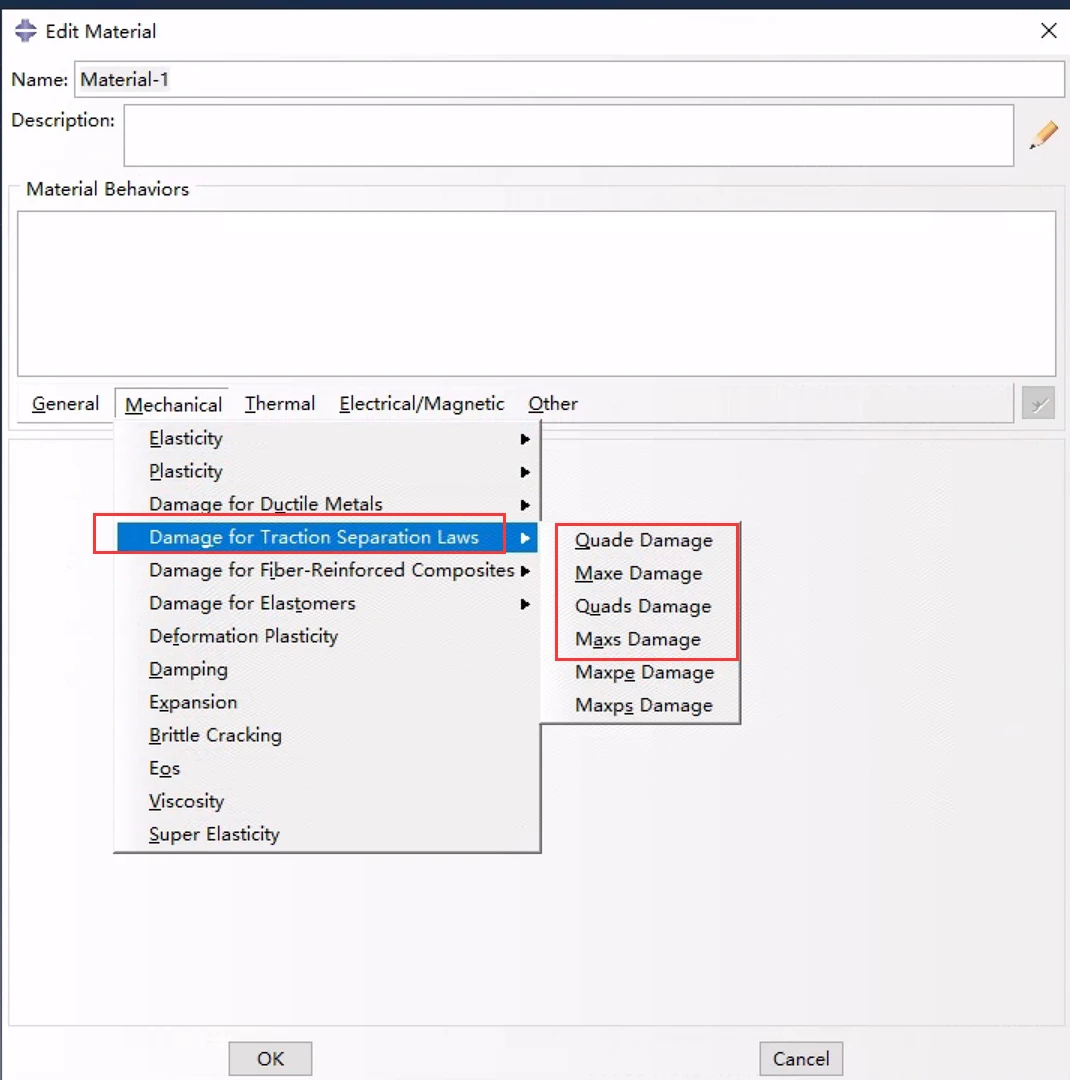
以上四种方法中,最大名义应力准则和二次名义应力准则(更保守,推荐)常用,而最大名义应变准则和二次名义应变准则不常用。另外,CAE中还有两种起始准则,Maxpe Damage最大主应变损伤和Maxps Damage最大主应力损伤,这两种主要是在扩展有限元模拟不连续体如裂纹问题时使用。
7. 损伤演化
损伤演化规律描述了达到相应起始准则后材料刚度退化的速率。标量损伤变量D表示材料的整体损伤,并捕获所有有效机制的综合影响。它最初的值是0。如果对损伤演化进行建模,则在损伤发生后的加载过程中,D单调地从0演化到1。牵引-分离模型的应力分量受到损伤的影响:

牵引应力分量的损伤演化
其中,¯t n、¯t s和¯t t为当前应变无损伤时的弹性牵引分离行为预测的应力分量。
为了描述界面上法向和剪切变形共同作用下的损伤演化,有必要引入有效位移(Camanho and Davila, 2002),其定义为:
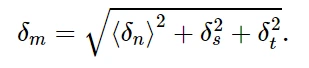
有效位移
7.1 混合模式定义
黏结区内变形场的模式组合量化了法向和剪切变形的相对比例。Abaqus使用三种模式混合度量,其中两种基于能量,另一种基于牵引力。当指定损伤演化过程的模式依赖性时,可以选择其中一种度量。分别用G n、G s、G t表示牵引力所做的功及其在法向、第一、第二剪切方向上的共轭相对位移,定义G T = G n + G s + G t,基于能量的模态混合定义如下:

显然,上面定义的三个量中只有两个是独立的。定义G S = G s + G t表示剪切牵引力所做的总功的部分和相应的相对位移分量。Abaqus要求指定与损伤演化相关的材料属性作为 m2 + m3 (= G S / G T) (或等价地,1 - m1)和m3 / (m2 + m3) (= G T / G S)的函数。
Abaqus根据变形的当前状态(能量的非累积度量)或基于变形历史(能量的累积度量)在一个积分点计算上述能量。前一种方法在混合模式模拟中是有用的,其中初级能量耗散机制与由于黏聚区失效而产生的新表面有关。这类问题通常是利用线弹性断裂力学的方法来充分描述的。后一种方法提供了定义模式混合的另一种方法,在其他重要的耗散机制也支配整体结构响应的情况下可能是有用的。
基于牵引力分量的模式混合的相应定义为:
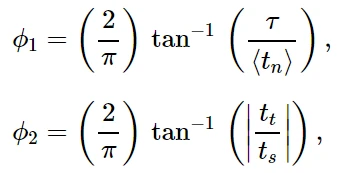
其中

是有效剪切牵引力的量度。在上述定义中使用的角度量(在它们被2 / π归一化之前)如图2所示。
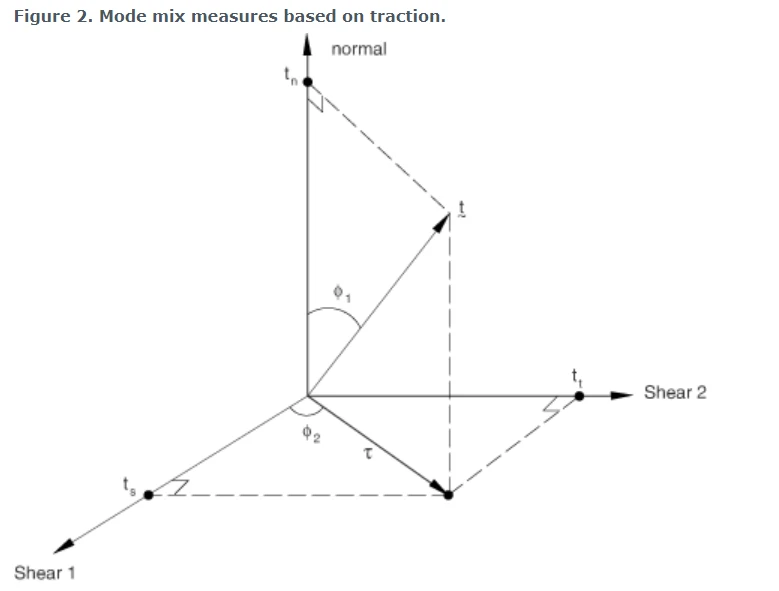
图2 基于牵引的模式混合度量
定义方法:

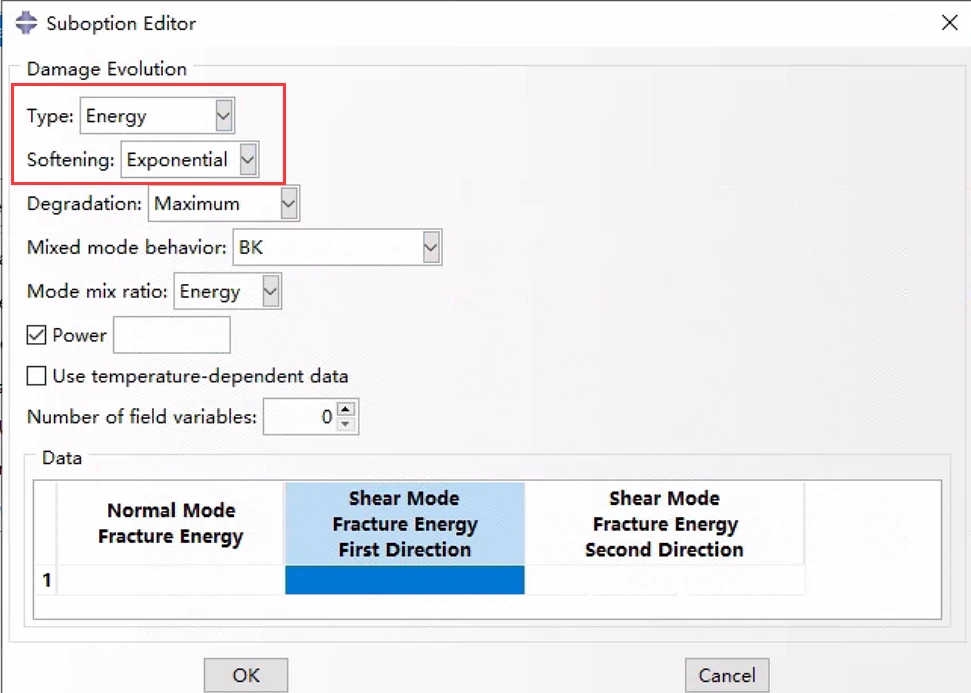
首先选择一种起始准则:
然后在子选项中选择:损伤演化
确认模式混合比采用能量还是牵引力方式:
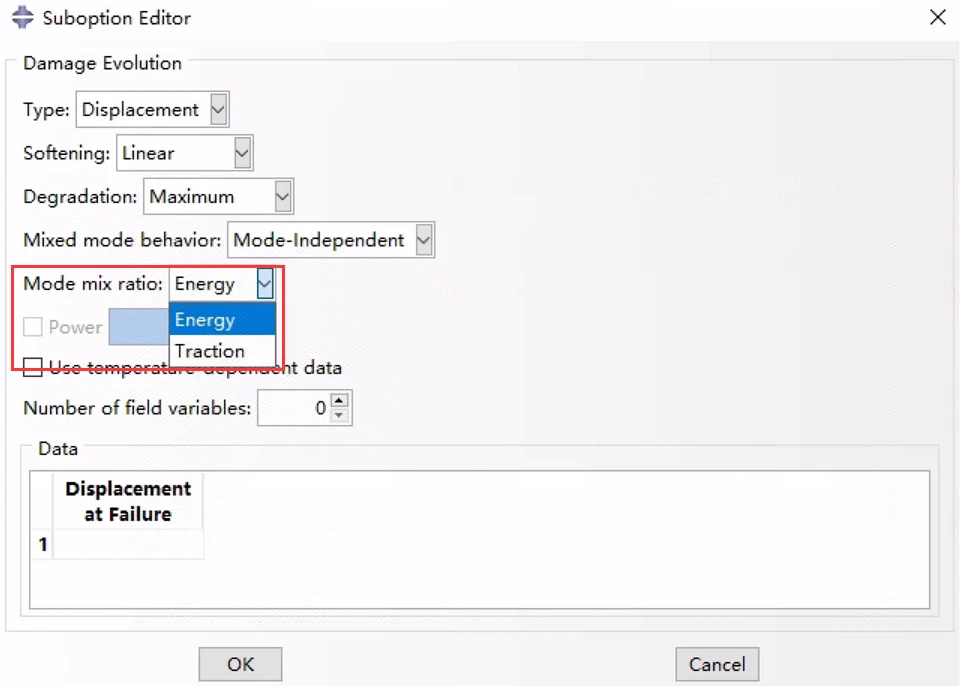
注意:在Abaqus/CAE中不支持根据累积能量定义模式混合。
混合模式定义的比较:
用不同的能量和牵引力来定义的模式混合比通常会有很大的不同。下面的例子说明了这一点。在能量方面,纯法线方向上的变形是Gn≠0且G s = G t = 0的变形,与法线和剪切牵引力的值无关。特别地,对于具有耦合牵引分离行为的材料,在纯法线方向上的变形,法向和剪切牵引都可能是非零的。在这种情况下,基于能量的模态混合定义将表明纯法向变形,而基于牵引力的定义将表明法向变形和剪切变形的混合。
当基于累积能量定义混合模式时,可能会在混合模式行为中引入人工路径依赖,这可能与基于线弹性断裂力学的预测不一致。因此,如果一个界面先纯法向加载,然后卸载,再纯剪切加载,则基于上述变形路径末端累积能量的模式混合比(假设剪切变形仅在local-1方向)为G n≠0,G s≠0。另一方面,在上述变形路径结束时,基于非累积能量的模式混合比取值为Gn = 0, G s≠0。
7.2 损伤演化的定义
损伤演化的定义有两个组成部分。
第一个需要定义完全破坏时的有效位移δ f m,相对于损伤开始时的有效位移δ o m;或因失效而耗散的能量G C(见图3)。
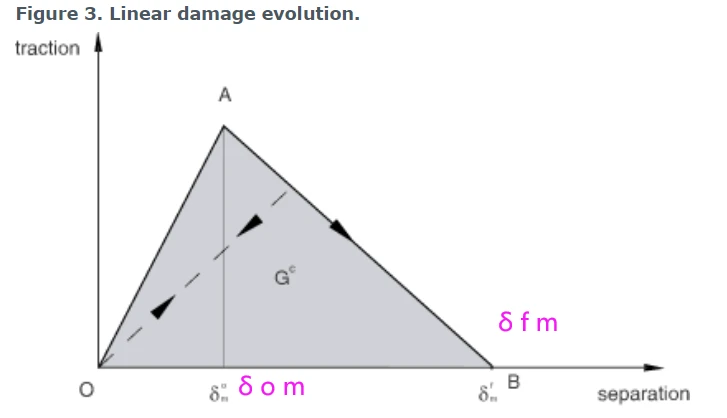
图3 线性损伤演化
损伤演化定义的第二个组成部分是对损伤变量D在损伤开始和最终破坏之间的演化性质的规定。这可以通过定义线性或指数软化定律或将D直接指定为有效位移相对于损伤开始时有效位移的表格函数来实现。上述材料数据通常是模态混合、温度和/或场变量的函数。
图4是具有各向同性剪切行为的牵引-分离响应的损伤起始和演化依赖于模式混合的示意图。图中显示了纵轴上的牵引力,以及两横轴上的法向分离和剪切分离的大小。两个垂直坐标平面上的无阴影三角形分别表示纯法向和纯剪切变形下的响应。所有中间垂直平面(包含纵轴)表示不同模式混合条件下的损伤响应。损伤演化数据对模式混合的依赖关系可以用表格形式定义,也可以用基于能量的解析定义。将损伤演化数据指定为模态混合函数的方式将在后面讨论。
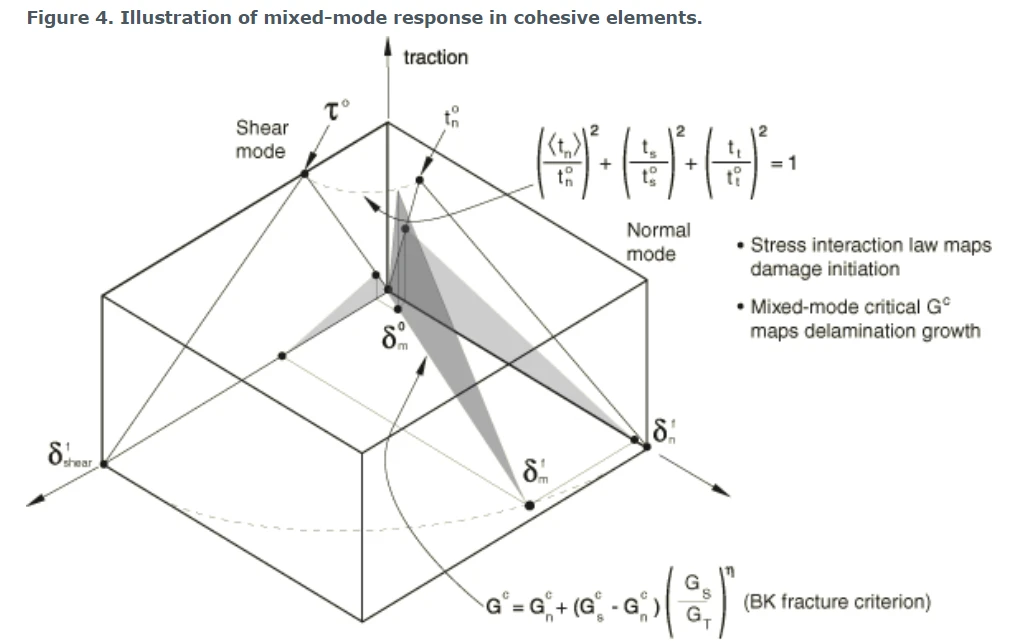
图4 粘聚力单元的混合模式响应说明
损伤开始后的卸载总是假设沿牵引分离平面的原点线性发生,如图3所示。卸载后的重新加载也沿着相同的线性路径进行,直到达到软化包络线(AB线)。一旦达到软化包络线,进一步的重新加载将按照图3中的箭头所示的包络线进行。
7.3 基于有效位移的演化
可以指定δ f m - δ om(即完全破坏时的有效位移δ f m,相对于损伤开始时的有效位移δ o m,如图3所示)作为模式混合、温度和/或场变量的表格函数。此外,还可以选择线性或指数软化律来定义损伤变量D的详细演化(从开始到完全破坏),作为损伤开始后有效位移的函数。或者,不使用线性或指数软化,可以将损伤变量D直接指定为损伤开始后有效位移δ m−δ o m、混合模式、温度和/或场变量的表格函数。
7.3.1 线性损伤演化
对于线性软化(见图3),Abaqus使用损伤变量D的演化,将(在恒定模式混合、温度和场变量下的损伤演化)简化为Camanho和Davila(2002)提出的表达式,即:
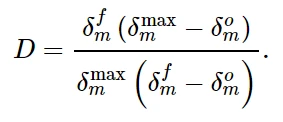
线性损伤演化损伤变量
δ max m是指在加载过程中获得的有效位移的最大值。对于涉及单调损伤(或单调断裂)的问题,通常假设在损伤开始和最终破坏之间的材料点处存在恒定模式混合。
线性损伤演化
7.3.2 指数损伤演化
对于指数软化(见图5),Abaqus使用损伤变量D的演化;在恒定模式混合、温度和场变量下的损伤演化情况下它将减小为:

指数损伤演化的损伤变量
α是定义损伤演化速率的无量纲材料参数,exp (x)是指数函数。
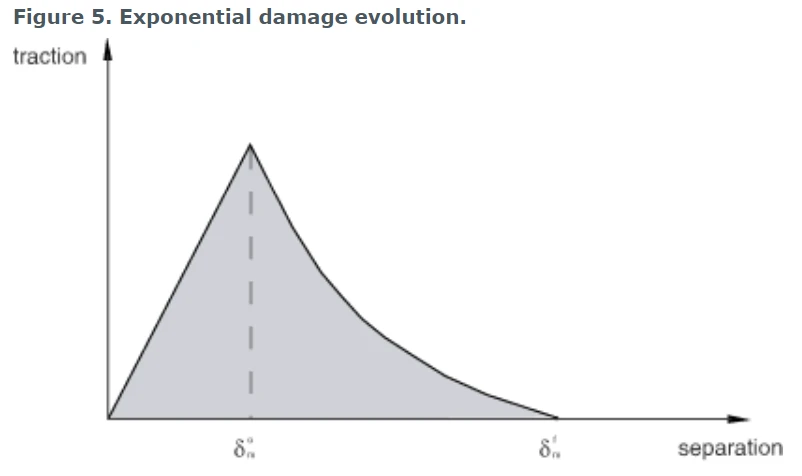
图5 指数损伤演化
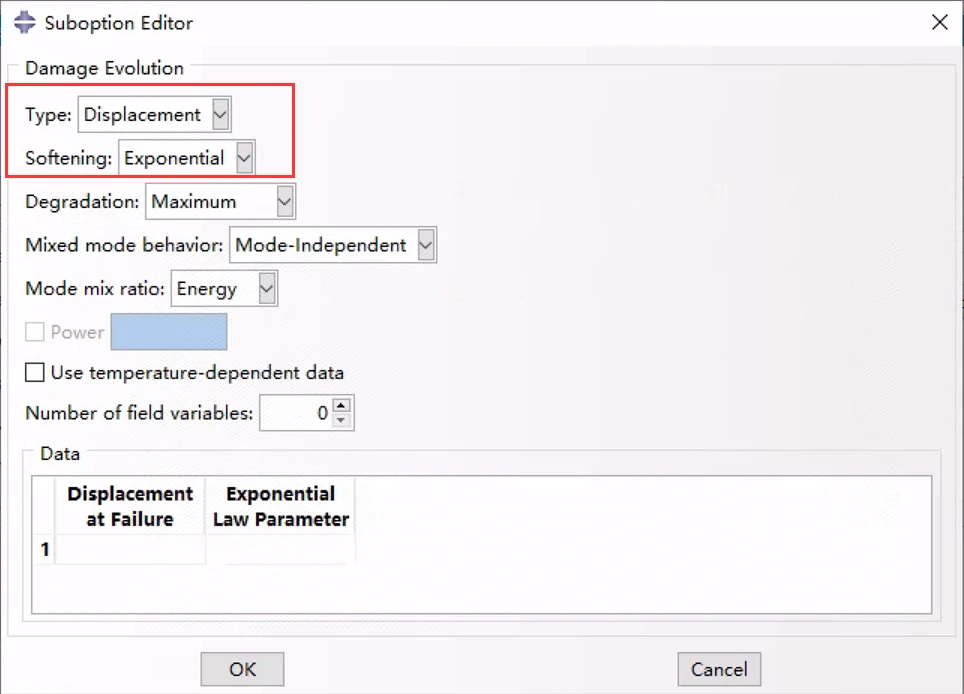
指数损伤演化的CAE定义
7.3.3 表格损伤演化
对于表格软化,可以直接以表格形式定义D的演变。D必须指定为有效位移相对于起始时的有效位移、模式混合、温度和/或场变量的函数。

表格损伤演化的定义
7.4 基于能量的演化
损伤演化可以根据损伤过程耗散的能量来定义,也称为断裂能。断裂能等于牵引-分离曲线下的面积(见图3)。将断裂能指定为材料属性,并选择线性或指数软化行为。Abaqus保证了线性或指数损伤响应下的面积等于断裂能。
断裂能对模式混合的依赖可以直接用表格形式表示,也可以用下面描述的解析形式表示。当使用解析形式时,假定模式混合比是用能量来定义的。
7.4.1 表格形式
定义断裂能相关性的最简单方法是将其直接指定为模式混合的函数。
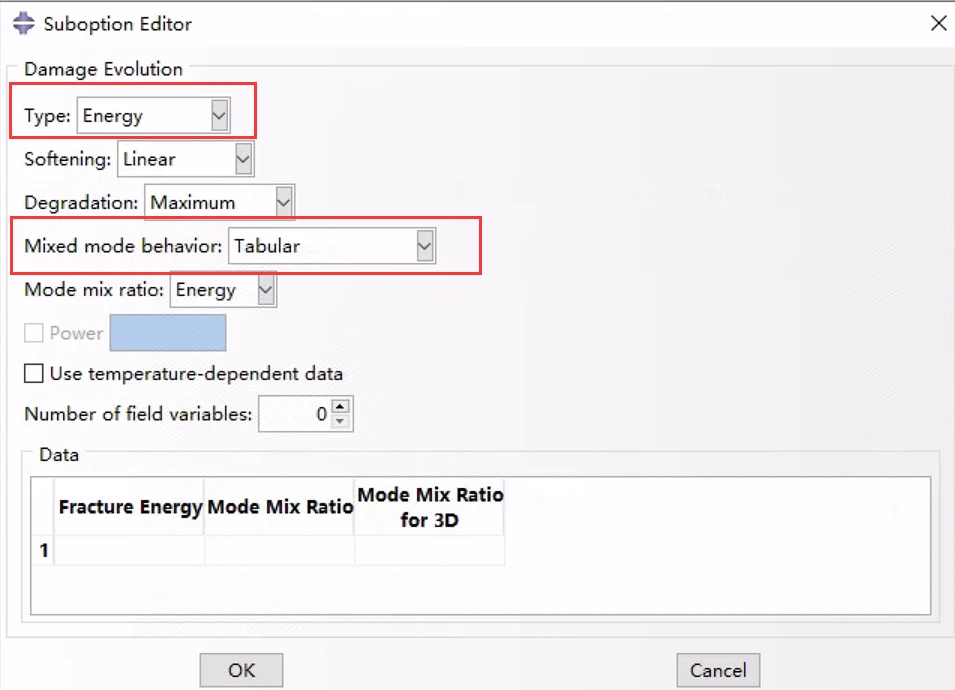
表格形式
7.4.2 幂律形式
断裂能对模式组合的依赖关系可以根据幂律断裂准则来定义。幂律准则指出,混合模式下的破坏是由单个(法向和双剪切)模式下导致破坏所需能量的幂律相互作用所控制的。
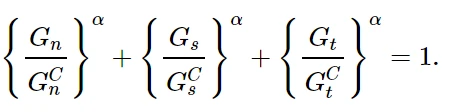
满足上述条件时,混合模式断裂能G C = G T。换句话说,
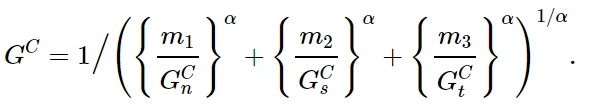
G C n, G C s和G C t是指在法向,第一和第二剪切方向上导致破坏所需的临界断裂能。
幂律形式
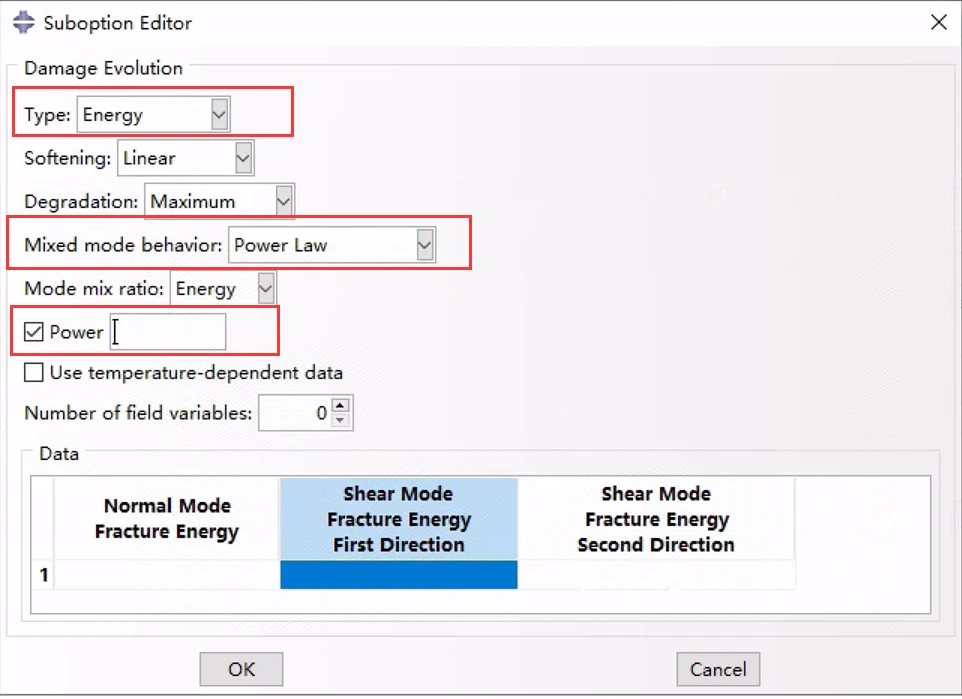
7.4.3 Benzeggagh-Kenane (BK)形式
Benzeggagh-Kenane断裂准则(Benzeggagh and Kenane, 1996)在纯沿第一和第二剪切方向变形时的临界断裂能相同时特别有用,即G C s = G C t。
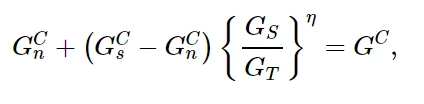
其中,
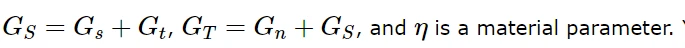
需要指定:
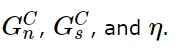
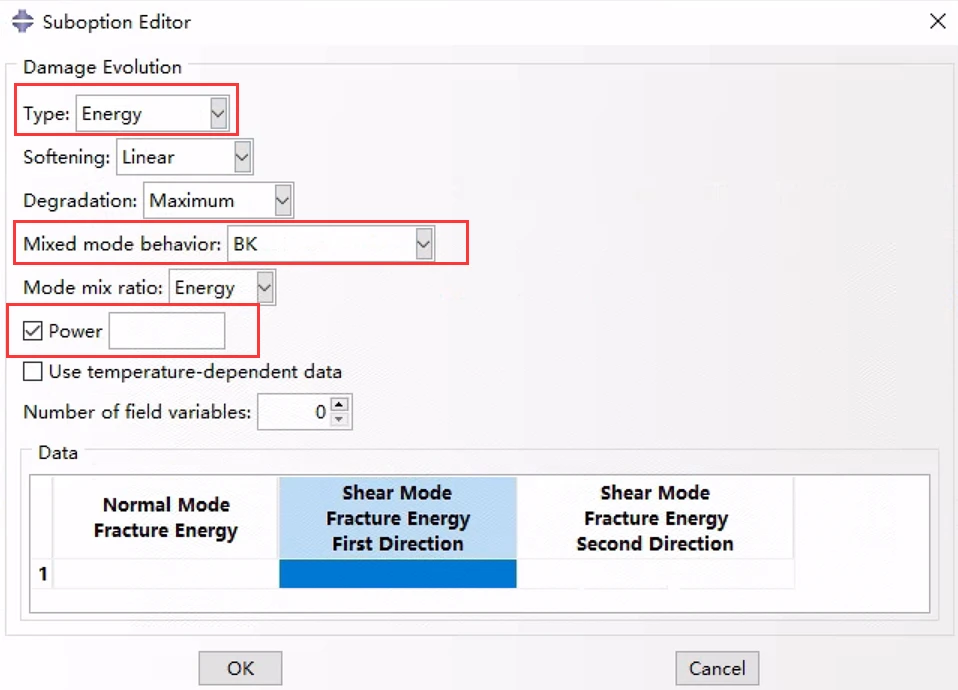
BK形式
7.4.4 线性损伤演化
对于线性软化(见图3),Abaqus使用损伤变量D的演化,其可降为:

其中
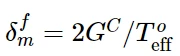
T o eff为损伤起始时的有效牵引力;δ max m指在加载过程中所获得的有效位移的最大值。

线性演化
7.4.5 指数损伤演化
对于指数软化,Abaqus使用损伤变量D的演化,它可以简化为:
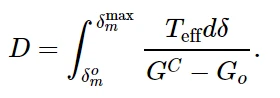
式中T eff为有效牵引力,δ为有效位移。G o为损伤起始时的弹性能。在这种情况下,牵引力可能不会在损伤开始后立即下降,这与图5所示的情况不同。
指数损伤演化
7.5 将损伤演化数据定义为模式混合的表格函数
对于基于能量的模式混合定义,在具有各向异性剪切行为的三维变形状态的最一般情况下,断裂能G C必须定义为(m2 + m3)和[m3 / (m2 + m3)]的函数。(m2 + m3) = G S / G T表示剪切变形占总变形的比例,而[m 3 / (m2 + m3)] = G T / G S表示第二剪切方向的总剪切变形占总剪切变形的比例。图6显示了断裂能与模式混合行为的示意图。
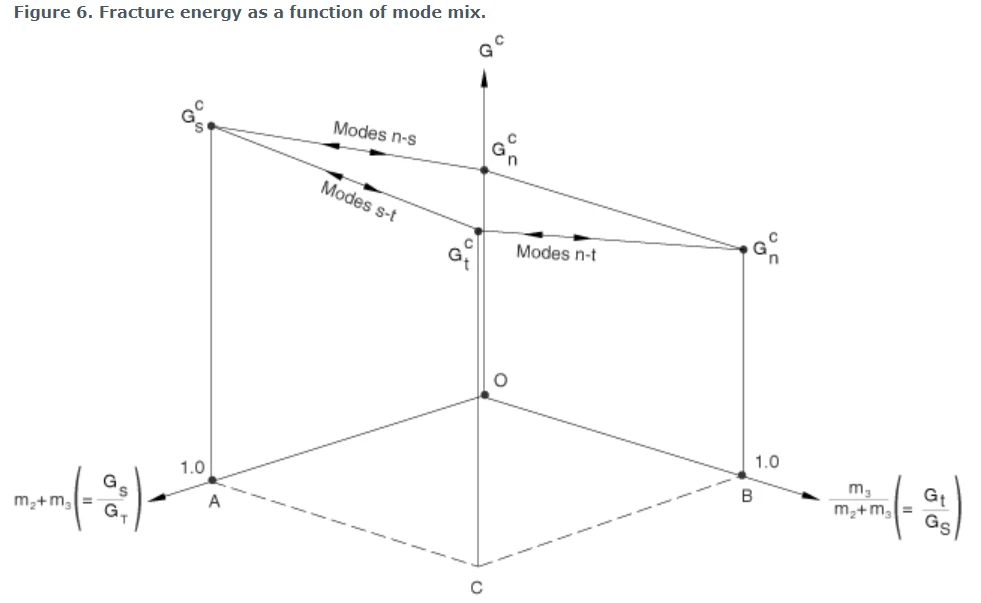
图6 断裂能是模式混合的函数
纯法向和纯剪切变形在第一和第二剪切方向的极限情况分别用G C n、G C s和G C t表示,如图6所示。“Modes n-s”、“Modes n-t”和“Modes s-t”分别表示纯法向和纯剪切在第一个方向、纯法向和纯剪切在第二个方向、纯剪切在第一个方向和第二个方向之间的行为转变。一般来说,必须将G C指定为[m3 / (m2 + m3)]的各种固定值下(m2 + m3)的函数。在接下来的讨论中,将与固定的[m3 / (m2 + m3)]对应的G C与(m2 + m3)的数据集称为“数据块”。将断裂能定义为模式混合的函数时,以下准则是有用的:
① 对于二维问题,只需将G C定义为m2的函数(在这种情况下,m3 = 0)。[m3 / (m2 + m3)]对应的数据列必须为空。因此,基本上只需要一个“数据块”。
② 对于具有各向同性剪切响应的三维问题,剪切行为由总和(m2 + m3)定义,而不是由m2和m3的单独值定义。因此,在这种情况下,单个“数据块”([m3 / (m2 + m3)] = 0时的“数据块”)也足以将断裂能定义为模态混合的函数。
③ 在具有各向异性剪切行为的三维问题的最一般情况下,需要几个“数据块”。如前所述,每个“数据块”将包含固定值[m3 / (m2 + m3)]的G C与 (m2 + m3)。在每个“数据块”中(m2 + m3)可以在0和1.0之间变化。(m2 + m3) = 0(任何“数据块”中的第一个数据点)对应于纯法向模态,当[m3 / (m2 + m3)]≠0时(即图6中OB线上唯一有效的点是O点,对应于纯法向变形)永远无法实现。然而,在将断裂能定义为模态混合函数的表格中,该点仅用于设置一个极限,以确保在从各种法向变形和剪切变形的组合接近纯法向状态时,断裂能连续变化。因此,每个“数据块”中第一个数据点的断裂能必须始终设置为等于纯法向变形模式下的断裂能(G C n)。
作为各向异性剪切情况的一个例子,考虑想要输入三个“数据块”,对应于固定值[m3 / (m2 + m3)] = 0,0.2和1.0。对于三个“数据块”中的每一个,由于上述原因,第一个数据点必须是(G C n, 0)。每个“数据块”中的其余数据点定义了随着剪切变形比例的增加,断裂能的变化。
基于牵引力的模式混合为:
断裂能需要以G C与φ 1和φ 2的表格形式指定。因此,需要将G C指定为φ 1在φ 2的各个固定值处的函数。在这种情况下,“数据块”对应于一组G C与φ 1的数据,其中φ 2为固定值。在每个“数据块”中,φ 1可以从0(纯法向变形)变化到1(纯剪切变形)。一个重要的限制是,每个数据块必须指定相同的断裂能量值φ 1 = 0。这一限制确保了当牵引矢量接近法线方向时所需的断裂能量不依赖于牵引矢量在剪切平面上的投影方向(见图2)。
当多个起始准则被激活时评估损伤:
当对同一材料使用多个损伤起始准则和相关的演化定义时,每个演化定义都会产生自己的损伤变量d1,其中下标i表示第i个损伤系统。整体损伤变量D是基于个体损伤di来计算的,正如在多个标准有效时评估整体损伤中所解释的那样。
8. 最大退化与单元删除
可以控制Abaqus如何处理具有严重损伤的粘聚力单元。默认情况下,材料点处整体损伤变量的上界为d max = 1.0。也可以降低这个上限。当损害达到这个极限时,可以控制粘聚力单元:
默认情况下,一旦整体损伤变量在其所有材料点处达到Dmax,且其所有材料点均不处于压缩状态,则除孔隙压力粘聚力单元外,其余粘聚力单元均被移除(删除)。这种单元删除的方法通常适用于模拟键的完全断裂和组件的分离。一旦移除,粘聚力单元就不会对组件的后续渗透提供任何阻力,因此可能有必要对组件之间的接触进行建模。
或者,可以指定粘聚力单元保留在模型中,即使在整体损伤变量达到Dmax之后。在这种情况下,单元在拉伸和/或剪切下的刚度保持不变(在初始未损坏刚度的基础上降低1 - D max)。这种选择是合适的,如果粘聚力单元必须抵抗周围组件的相互渗透,即使他们的张力和/或剪切已经完全退化。在Abaqus/Explicit中,建议通过使用section控件将线性和二次体粘度参数的比例因子设置为零来抑制粘聚力单元中的体粘度。
9. 非耦合横向剪切响应
可选择定义线弹性横向剪切行为,以提供粘聚力单元额外的稳定性,特别是在损坏发生后。横向剪切行为被认为是独立于常规的材料响应,不经历任何破坏。

通过输入文件定义,CAE不支持
10. Abaqus/Standard中的粘性正则化
在Abaqus/Standard等隐式分析求解中,表现出软化行为和刚度退化的材料模型经常导致严重的收敛困难。克服这些收敛困难的一种常用技术是使用本构方程的粘性正则化,这使得软化材料的正切刚度矩阵在足够小的时间增量内为正。
在Abaqus/Standard中,通过允许应力超出牵引-分离律所设定的限制,可以使用粘度对牵引-分离律进行正则化。正则化过程涉及到使用粘性刚度退化变量Dv,它由演化方程定义:
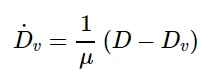
其中,μ为粘性系统松弛时间的粘性参数,D为无粘骨架模型的退化变量。
粘性材料的损伤响应为:
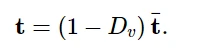
使用较小的粘性参数值(与特征时间增量相比较小)的粘性正则化通常有助于提高模型在软化状态下的收敛速度,而不会影响结果。其基本思想是,粘性系统的解松弛为t / μ→∞,其中t表示时间。可以指定粘度参数的值,作为部分控制定义的一部分。如果黏度参数不等于零,则输出的刚度退化结果为黏度值Dv。粘度参数的默认值为零,因此不执行粘性正则化。在层合复合材料的分层分析和蒙皮加筋在张力作用下的脱粘分析中,讨论了利用粘性正则化来改善分层和脱粘问题的收敛性。通过使用输出变量ALLCD,可以获得与整个模型或元素集上的粘性正则化相关的近似能量。
11. 输出
除了Abaqus中可用的标准输出标识符之外,以下变量对于具有牵引分离行为的内聚元素具有特殊意义:
STATUS:单元的状态(如果单元有效,状态是1.0;如果单元失效,状态是0.0)。
SDEG:标量损伤变量D的总体值。
DMICRT:所有损伤起始标准分量。
MAXSCRT:在分析过程中,在材料点处的名义应力损伤起裂准则的最大值。
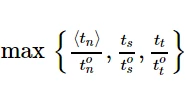
MAXECRT:在分析过程中,在材料点处的名义应变损伤起裂准则的最大值。
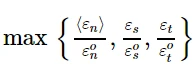
MMIXDME:损伤演化过程中的模式混合比。它的值是1 - m1。一般来说,它在给定的积分点随时间变化。在开始损坏之前,该变量设置为−1.0。
MMIXDMI:损伤开始时的模式混合比。在第一次积分点损伤开始时,其值为1−m1。它在给定的积分点随时间保持不变。在开始损坏之前,该变量设置为−1.0。
QUADSCRT:在分析过程中,材料点处二次名义应力损伤起裂准则的最大值。
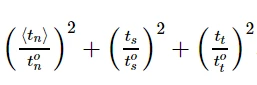
max
QUADECRT:在分析过程中,材料点处的二次名义应变损伤起裂准则的最大值。
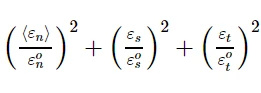
max
ALLCD:在Abaqus/Standard中与粘性正则化相关的整个模型或单元集上的能量的近似量。相应的输出变量(如CENER、ELCD、ECDDEN)分别表示积分点级和单元级与粘性正则化相关的能量(最后一个量表示单元中单位体积的能量)。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删