cohesive建模技术可应用于粘合剂、粘结界、复合材料以及岩石断裂。
其中常用的基于cohesive粘聚力模型的建模方法有两种,一个是采用粘聚力单元(cohesive 单元)建模,一个是定义粘聚力接触。这两种方法对应的粘聚力模型理论是相同的,仅在具体操作设置及应用场景有差别。
下面首先来学习粘聚力模型的基本理论中最简单的双线性本构模型:
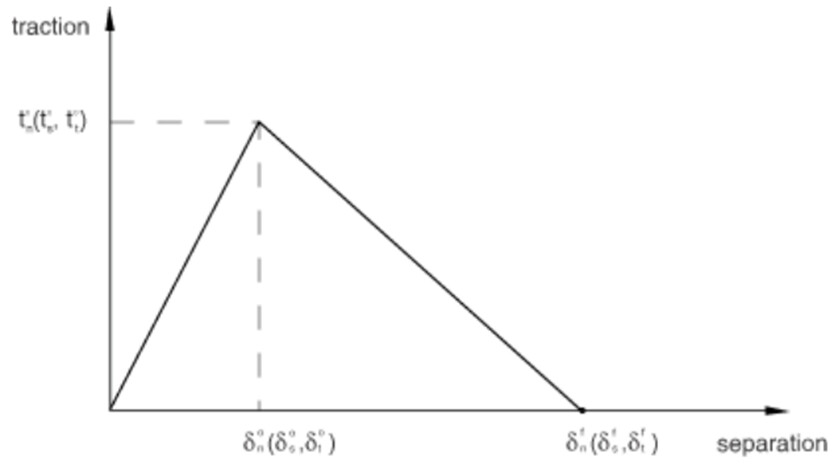
双线性本构模型
粘聚力模型主要用来描述厚度方向以及垂直厚度方向(两个切向)的力学行为。上图中双线性本构模型描述了粘结层的受力特性,其中竖轴为力,横轴为位移,上图展示的就是粘结层受力时随位移先增大后减少的现象。其中峰值后的力学行为称为损伤后的力学行为(损伤演化)。即在峰值前材料是线弹性的,一旦超过峰值点,就会有刚度退化的现象,如下图所示。
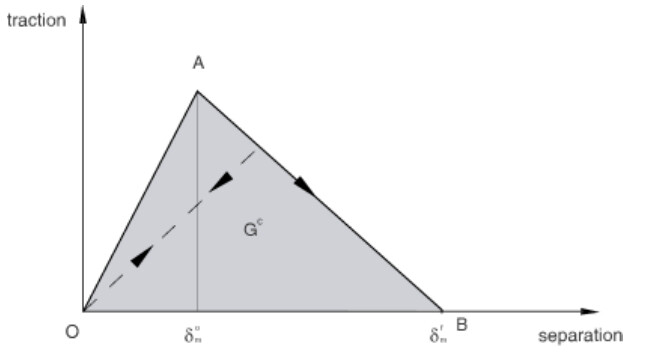
过峰值点后再加载力学行为
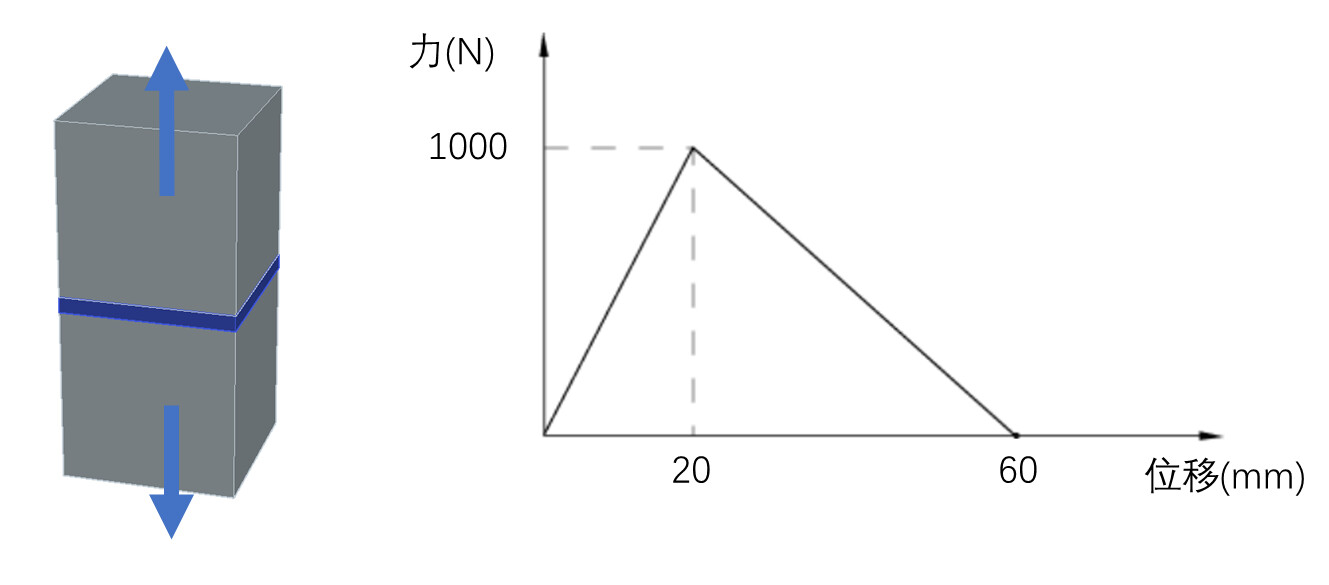
假设某粘结层拉伸试验如下图所示,得到的实验数据如右图,那么我们就得到了厚度方向上的力学行为曲线,同样可以做两个切向的试验得到切向的行为曲线,有了这三条曲线我们就可以知道当粘结层具体受力时会发生怎么样的行为。接下来就是要告诉Abaqus某些参数,当Abaqus得到这些参数后能还原本构曲线。双线性本构比较简单,就是一个三角形,我们可以告诉初始斜率,峰值力以及整个三角形面积,这种方法就是基于能量的方法。还可以告诉初始斜率,峰值力以及破坏时的位移,这种就是基于位移的损伤演化方法。
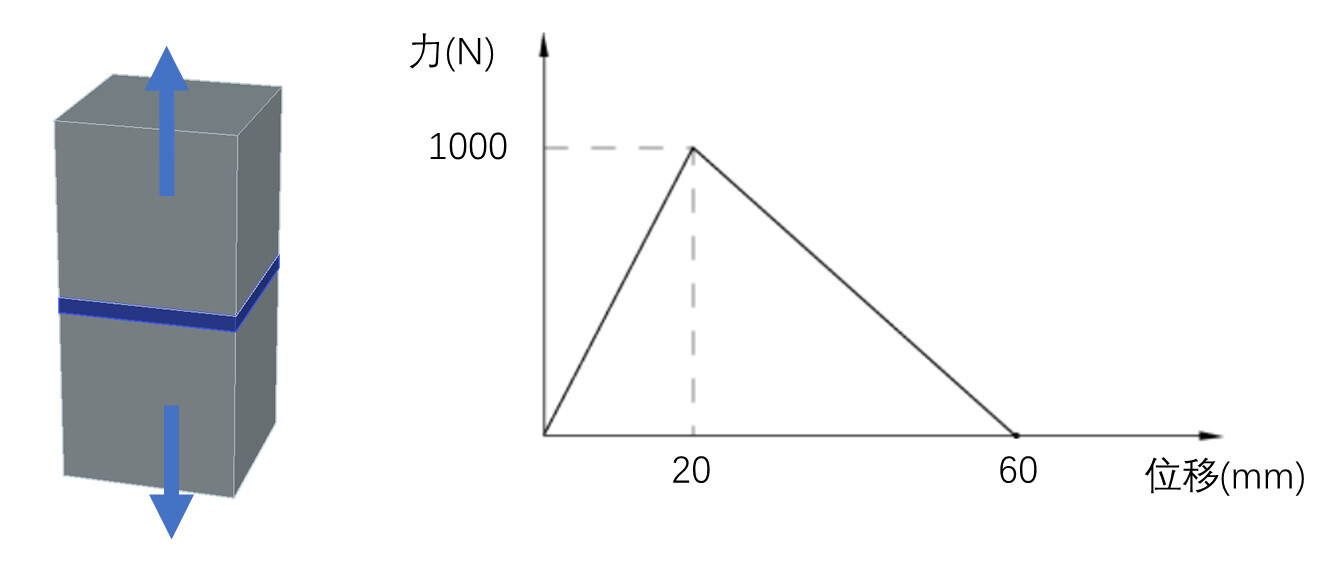
目前还有一个问题就是我们只知道单一方向下的力学行为,但是当材料同时受剪切与拉伸时什么时候开始损伤我们是不知道的。这就涉及到判断准则。常用的有两种,最大名义应力准则和二次名义应力准则。
最大名义应力准则就是说只要某一个方向的力达到最大值后,材料就开始损伤,如下图所示。
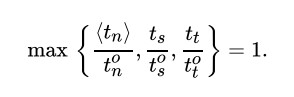
最大名义应力准则
二次名义应力准则如下图,三个方向的平方和等于1时就到达了损伤判据。
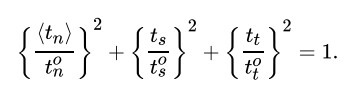
二次名义应力准则
对比可已发现其中二次名义准则较最大名义应力准则更加保守。当然还有应变准则,在此不过多介绍了。
下面我们就以下图这个实例告诉你基于能量方法中试验数据与Abaqus参数对应关系。假设试验时我的上下两块立方体边长为1m,拉伸工况,那么使用国际单位制下斜率为:
同样的两个方向的剪切工况也可以做出来,得到上述参数。
其中knn对应材料属性中的Enn,而Ess,Ett为另外两个剪切方向的试验结果。
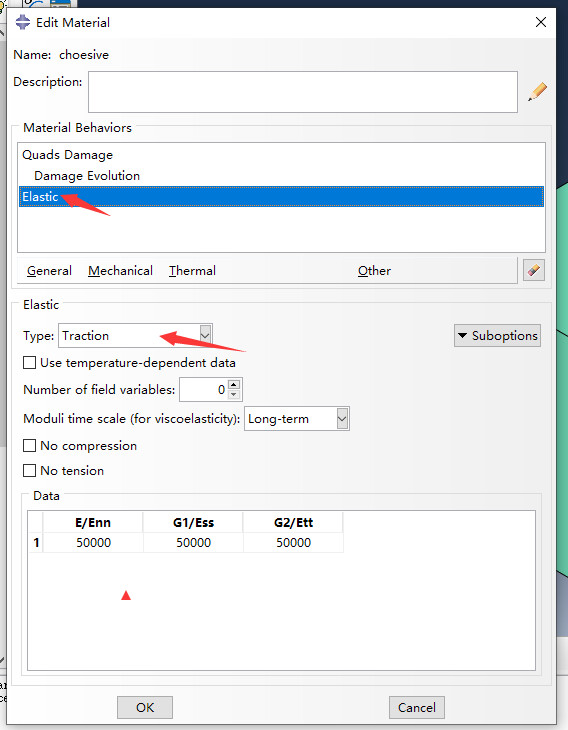
三方向刚度
其中σnn对应材料属性中的第一个参数,其余两个参数为另外两个剪切方向的试验结果。
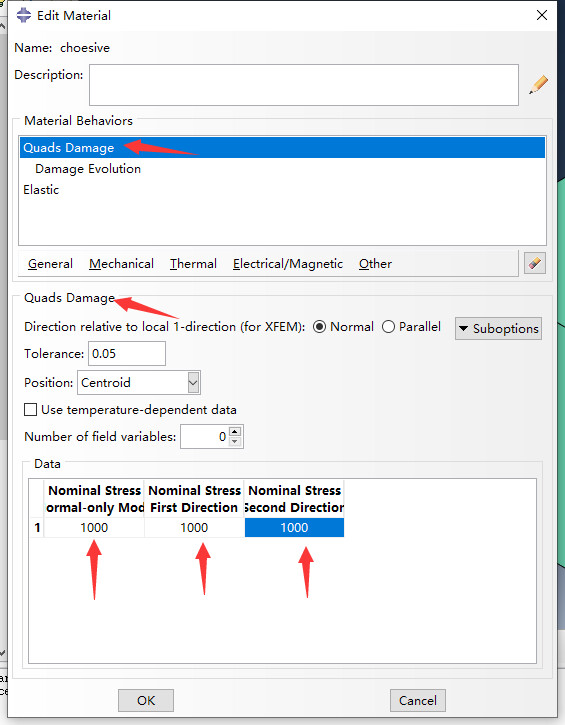
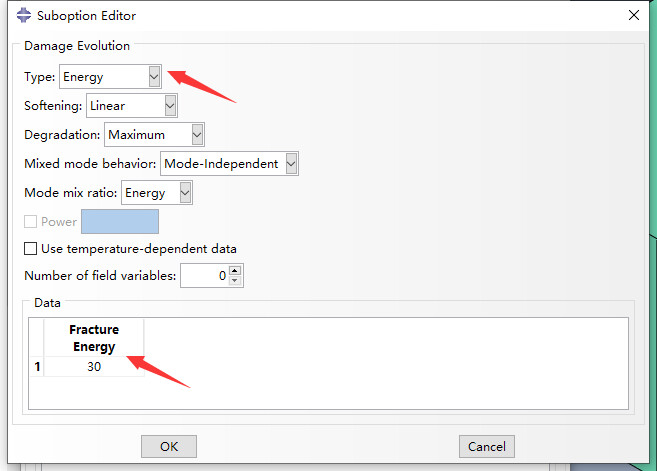
而三角形面积对应断裂能
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删