随着时代的进步, 人们的生活水平和生活质量都在不断地提高,追求 完美日益成为时尚。对消费产品来说,人们在要求其具有完备的功能外, 越来越追求外形 的美观。因此,产品设计者在很多时候需要用复杂的曲面来表现产品的外观。本章将针对曲 面对设计进行概要性讲解
主要内容包括:曲面设计的发展概况、曲面设计的基本方法和应用技巧。与一般实体零件的创建相比,曲面的设计是较难掌握的部分,其技巧性比较强, 需要读者用心体会, 多加练习。

1.1 曲面设计的发展概况
曲面造型(Surface Modeling)是随着计算机技术和数学方法的不断发展而逐步产生和 完善起来的。它是计算机辅助几何设计(Computer Aided Geometric Design,简称 CAGD) 和计算机图形学(Computer Graphics)的一项重要内容,主要研究在计算机图像系统的环 境下, 对曲面的表达、创建、显示以及分析等。
早在 1963 年, 美国波音飞机公司的Ferguson 首先提出将曲线曲面表示为参数的矢量 函数方法,并引入参数三次曲线。从此曲线曲面的参数化形式成为形状数学描述的标准 形式。
到了 1971 年,法国雷诺汽车公司的 Bezier 又提出一种控制多边形设计曲线的新方法, 这种方法很好地解决了整体形状控制问题,从而将曲线曲面的设计向前推进了一大步。然 而 Bezier 的方法仍存在连接问题和局部修改问题。
直到 1975 年, 美国 Syracuse 大学的 Versprille 首次提出了具有划时代意义的有理 B 样 条(NURBS)方法。 NURBS 方法可以精确地表示二次规则曲线曲面, 从而能用统一的数字 学形式表示规则曲面与自由曲面。这一方法的提出,终于使非均匀有理 B 样条方法成为现 代表曲面造型中广泛流行的技术。
随着计算机图形技术以及工业制造技术的不断发展,曲面造型在近几年又得到了长足 的发展,这主要表现在以下几个方面。
(1)从研究领域来看, 曲面造型技术已从传统的研究曲面表示、曲面求交和曲面拼接, 扩充到曲面变形、曲面重建、曲面简化、曲面转换和曲面等距性等。
(2)从表示方法来看,以网格细分为特征的离散造型方法得到了广泛的运用。这种曲 面造型方法在生动逼真的特征动画和雕塑曲面的设计加工中更是独具优势。
(3)从曲面造型方法来看,出现了一些新的方法,如基于物理模型的曲面造型方法、
基于偏微分方程的曲面造型方法、流曲线曲面造型方法等。
当今在 CAD/CAM 系统的曲面造型领域, 有一些功能强大的软件系统。如美国 PTC 公 司的 Creo、美国 SDRC 公司的 I-DEASMasterSeries、美国 Unigraphics Solutions 公司的 UG 以及法国达索公司的 CATIA 等, 它们各具特色和优势, 在曲面造型领域都发挥着举足轻重 的作用。
美国 PTC 公司的 Creo,以其参数化、基于特征、全相关等新概念闻名于 CAD 领域。 它在曲面的创建生成、编辑修改、计算分析等方面功能强大。另外,它还可以将特殊的曲 面造型实例作为一个特征加入特征库中, 使其功能得到不断扩充。
1.2 曲面造型的数学概念
曲面造型技术随着数学相关研究领域的不断深入而得到长足的进步,多种曲线、曲面 被广泛应用。我们在此主要介绍其中最基本的一些曲线、曲面的理论及构造方法,使读者 在原理、概念上有一个大致的了解。
1. 贝塞尔(Bezier)曲线与曲面
Bezier 曲线与曲面是法国雷诺公司的 Bezier 在 1962 提出的一种构造曲线曲面的方法 法, 是三次曲线的形成原理, 这是由四个位置矢量 Q0、Q1、Q2、Q3 定义的曲线。通常将 Q0,Q1 ,… ,Qn 组成的多边形折线称为 Bezier 控制多边形, 多边形的第一条折线和最后 一条折线代表曲线起点和终点的切线方向,其他曲线用于定义曲线的阶次与形状。
2 . B 样条曲线与曲面
B 样条曲线继承了 Bezier 曲线的优点,仍采用特征多边形及权函数定义曲线,所不同 的是权函数不采用伯恩斯坦基函数, 而采用 B 样条基函数。
B 样条曲线与特征多边形十分接近, 同时便于局部修改。与 Bezier 曲面生成过程相似, 由 B 样条曲线可很容易地推广到 B 样条曲面。
3.非均匀有理 B 样条(NURBS)曲线与曲面
NURBS 是 Non-Uniform Rational B-Splines 的缩写, 是非均匀有理 B 样条的意思。具体 解释如下。
● Non-Uniform (非均匀):指一个控制顶点的影响力的范围能够改变。当创建一个 不规则曲面的时候,这一点非常有用。同样,统一的曲线和曲面在透视投影下也不是无变化的, 对于交互的 3D 建模来说,这是一个严重的缺陷。
● Rational (有理):指每个 NURBS 物体都可以用数学表达式来定义。
● B-Spline (B 样条): 指用路线来构建一条曲线,在一个或更多的点之间以内插值 替换。
NURBS 技术提供了对标准解析几何和自由曲线、曲面的统一数学描述方法, 它可通过 调整控制顶点和因子, 方便地改变曲面的形状, 同时也可方便地转换对应的 Bezier 曲面, 因此 NURBS 方法已成为曲线、曲面建模中最为流行的技术。 STEP 产品数据交换标准也将 非均匀有理 B 样条(NURBS)作为曲面几何描述的唯一方法。
4 . NURBS 曲面的特性及曲面连续性定义
(1)NURBS 曲面的特性。
NURBS 是用数学方法来描述形体, 采用解析几何图形, 曲线或曲面上任何一点都有其 对应的坐标(x,y,z),所以具有高度的精确性。NURBS 曲面可以由任何曲线生成。
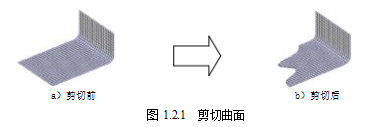
对于 NURBS 曲面而言, 剪切是不会对曲面的 UV 方向产生影响的,也就是说不会对 网格产生影响, 如图 1.2.1a 和图 1.2.1b 所示,剪切前后网格(U 方向和 V 方向) 并不会发 生实质的改变。这也是通过剪切四边面来构成三边面和五边面等多边面的理论基础。
(2)曲面 G1 与 G2 连续性定义。
Gn 表示两个几何对象间的实际连续程度。例如:
● G0 意味着两个对象相连或两个对象的位置是连续的。
● G1 意味着两个对象光滑连接,一阶微分连续, 或者是相切连续的。
● G2 意味着两个对象光滑连接,二阶微分连续, 或者两个对象的曲率是连续的。
● G3 意味着两个对象光滑连接,三阶微分连续。
● Gn 的连续性是独立于表示(参数化) 的。
1.3 曲面造型方法
曲面造型的方法有多种, 下面介绍最常见的几种方法。
1.拉伸面
将一条截面曲线沿一定的方向滑动所形成的曲面, 称为拉伸面,如图 1.3.1 所示。

2.直纹面
将两条形状相似且具有相同次数和相同节点矢量的曲线上的对应点用直线段相连,便 构成直纹面,如图 1.3.2 所示。圆柱面、圆锥面其实都是直纹面。

当构成直纹面的两条边界曲线具有不同的阶数和不同的节点时, 需要首先将次数或节点 数较低的一条曲线通过升阶、插入节点等方法,提高到与另一条曲线相同的次数或节点数, 再创建直纹面。另外,构成直纹面的两条曲线的走向必须相同,否则曲面将会出现扭曲。
3.旋转面
将一条截面曲线沿着某一旋转轴旋转一定的角度, 就形成了一个旋转面, 如图 1.3.3 所示。

4.扫描面
将截面曲线沿着轨迹曲线扫描而形成的曲面称为扫描面,如图 1.3.4 所示。
截面曲线和轨迹线可以有多条,截面曲线形状可以不同,可以封闭也可以不封闭,生
成扫描面时, 软件会自动过渡,生成光滑连续的曲面。

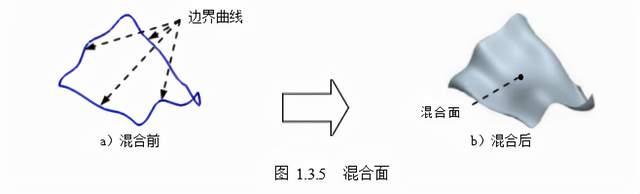
5.混合面
混合面是以一系列曲线为骨架进行形状控制,且通过这些曲线自然过渡生成的曲面, 如图 1.3.5 所示。
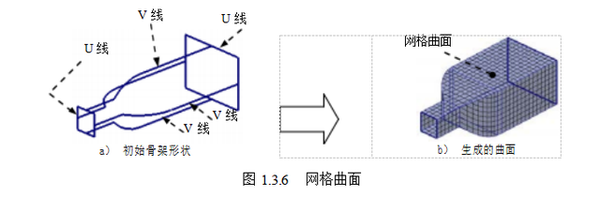
6. 网格曲面
网格曲面是在两组相互交叉、形成一张网格骨架的截面曲线上生成的曲面。网格曲面 生成的思想是首先构造出曲面的特征网格线(U 线和 V 线),比如, 曲面的边界线和曲面的截面线来确定曲面的初始骨架形状,然后用自由曲面插值特征网格生成曲面, 如图 1.3.6所示。
由于骨架曲线采用不同方向上的两组截面线形成一个网格骨架,控制两个方向的变化 趋势,使特征网格线能基本上反映出设计者想要的曲面形状,在此基础上, 插值网格骨架 生成的曲面必然将满足设计者的要求。
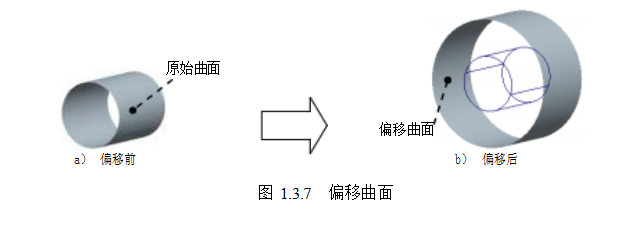
7. 偏移曲面
偏移曲面就是把曲面特征沿某方向偏移一定的距离来创建的曲面, 如图 1.3.7 所示。机械加工或钣金零件在装配时为了得到光滑的外表面,往往需要确定一个曲面的偏移曲面。现在常用的偏移曲面的生成方法一般是先将原始曲面离散细分,然后求取原始曲面离 散点上的等距点,最后将这些等距点拟合成等距面。
1.4 光滑曲面造型技巧
一个美观的产品外形往往是光滑而圆顺的。光滑的曲面,从外表看流线顺畅,不会引 起视觉上的凸凹感,从理论上是指具有二阶几何连续、不存在奇点与多余拐点、曲率变化 较小,以及应变能力较小等特点的曲面。
要保证构造出来的曲面既光滑又能满足一定的精度要求,就必须掌握一定的曲面造型 技巧, 下面我们就一些常用的技巧进行介绍。
1. 区域划分,先局部再整体
一个产品的外形,往往用一张曲面去描述是不切实际和不可行的,这时就要根据应用 软件曲面造型方法,结合产品的外形特点,将其划分为多个区域来构造几张曲面,然后再 将它们合并在一起, 或用过渡面进行连接。当今的三维 CAD 系统中的曲面几乎都是定义在 四边形域上。因此,在划分区域时,应尽量将各个区域定义在四边形域内, 即每个子面片 都具有四条边。
2. 创建光滑的控制曲线是关键
控制曲线的光滑程度往往决定着曲面的品质。要创建一条高质量的控制曲线,主要应 从以下几点着手:①要达到精度的要求;②曲率主方向要尽可能一致;③曲线曲率要大于 将作圆角过渡的半径值。
在创建步骤上,首先利用投影、插补、光滑等手段生成样条曲线,然后根据其曲率图 的显示来调整曲线段, 从而实现交互式的曲线修改,达到光滑的效果。有时也可通过调整 空间曲线的参数一致性, 或生成足够数目的曲线上的点,再通过这些点重新拟合曲线,以 达到使曲面光滑的目的。
3.光滑的连接曲面片
曲面片的光滑连接,应具备以下两个条件:①要保证各连接面片间具有公共边;②要 保证各曲面片的控制线连接光滑。其中第二条是保证曲面片连接光滑的必要条件,可通过 修改控制线的起点、终点的约束条件,使其曲率或切线在接点处保证一致。
4.还原曲面, 再塑轮廓
一个产品的曲面轮廓往往是已经修剪过的, 如果我们直接利用这些轮廓线来构造曲面, 常常难以保证曲面的光滑性,所以造型时要充分考察零件的几何特点,利用延伸、投影等技术 方法将三维空间轮廓线还原为二维轮廓线, 并未去掉细节部分, 然后还原出“原始”的曲面, 最后再利用面的修剪方法获得理想的曲面外轮廓。
5.注重实际, 从模具的角度考察曲面质量
再漂亮的曲面造型,如果不注重实际的生产制造, 也毫无用处。产品三维造型的最终 目的是制造模具。产品零件大多由模具生产出来, 因此,在三维造型时, 要从模具的角度 去考虑,在确定产品出模方向后,应检查曲面能否出模,是否有倒扣现象(即拔模斜度为 负值),如发现问题,应对曲面进行修改或重构曲面。
6.随时检查, 及时修改
在进行曲面造型时, 要随时检查所建曲面的状况, 注意检查曲面是否光滑、有无扭曲、 曲率变化等情况,以便及时修改。
检查曲面光滑的方法主要有以下两种:第一,对构造的曲面进行渲染处理, 可通过透 视、透明度和多重光源等处理手段产生高清晰度的逼真的彩色图像,再根据处理后的图像 光亮度的分布规律来判断出曲面的光滑度。图像明暗度变化比较均匀,则说明曲面光滑性 好。第二,可对曲面进行高斯曲率分析,进而显示高斯曲率的彩色光栅图像,这样可以直 观地了解曲面的光滑性情况。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删