ANSYS 19.2模态分析详解：概念、网格划分与模态设置

0.名词解释

模态的分类：有约束普通模态(对应大多数一般工况)、无约束自由模态(对应少数极端工况)

模态分析：是动力学分析的基础，简单来说是求频率、振型等固有特性。

X阶固有频率：模型的固有频率由低到高排列，依次为一阶固有频率、二阶固有频率等等

主振型：当将某个物体振幅设为1时求得的相对幅值比值称为主振型

X阶主振型：x阶固有频率的主振型幅值设为1时的振型

注意：

系统有多少自由度即有多少阶模态

连续弹性体理论上有无限多阶固有频率

1.网格的划分

在视频的1分30秒，点击mesh>insert>sizing后，在definition的type栏修改element size，

element size为2mm的结果如下所示

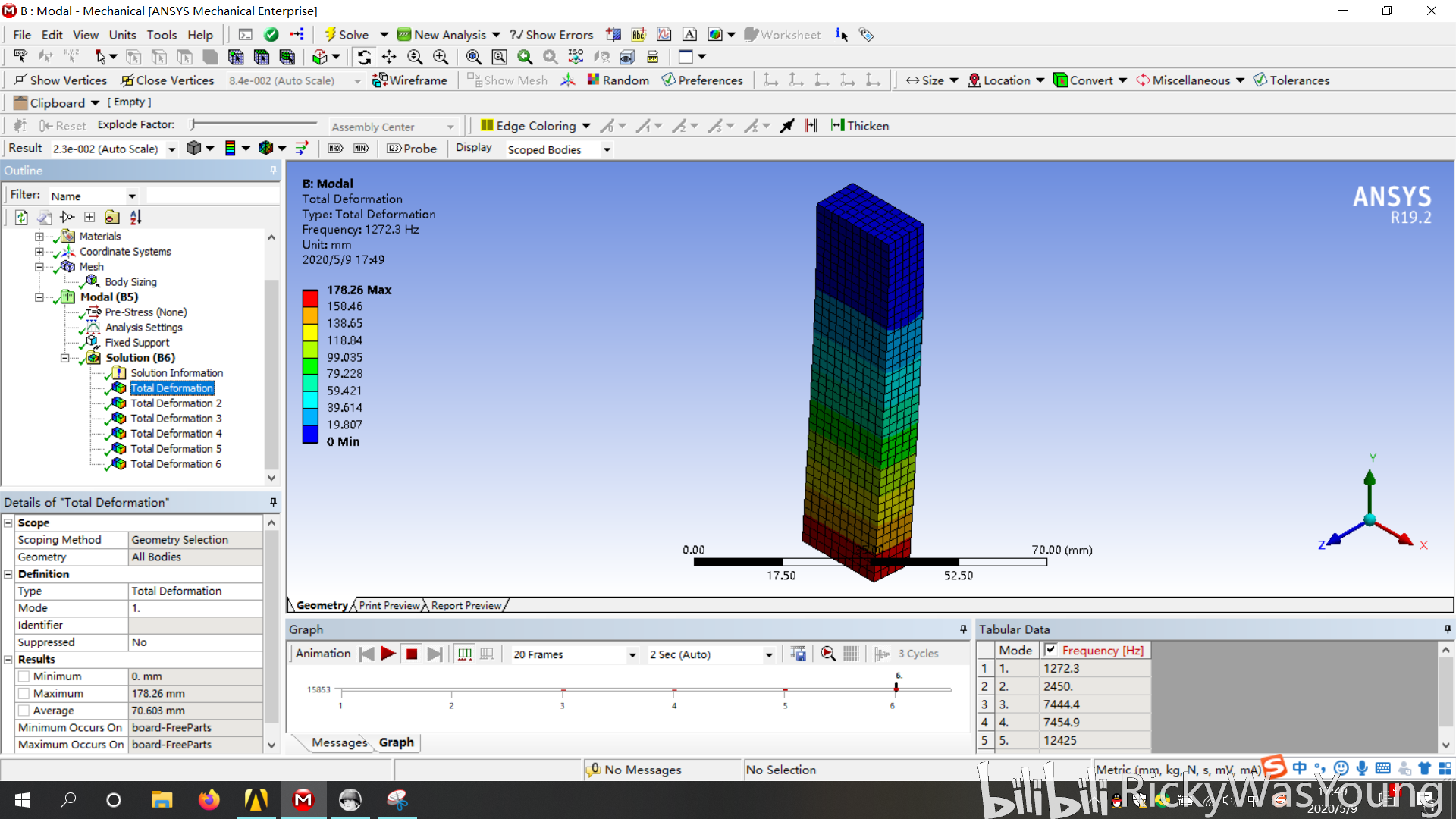
   2mm，一阶模态示意图
 

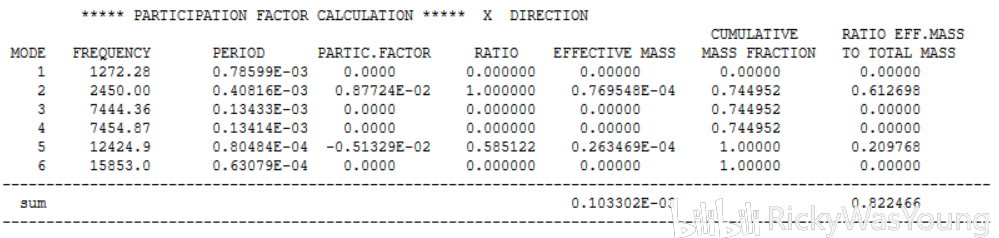
   2mm，x轴结果
 

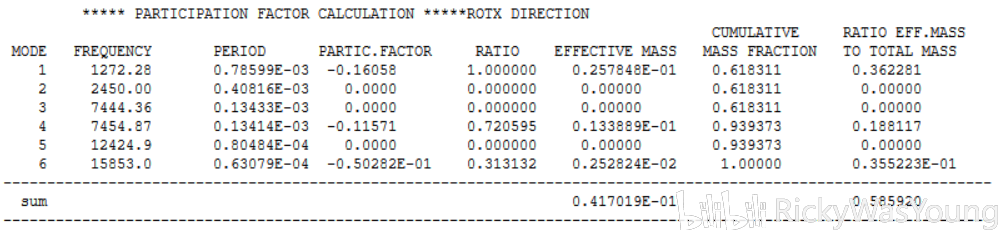
   2mm，x轴旋转结果
 

element size为3mm的结果如下所示

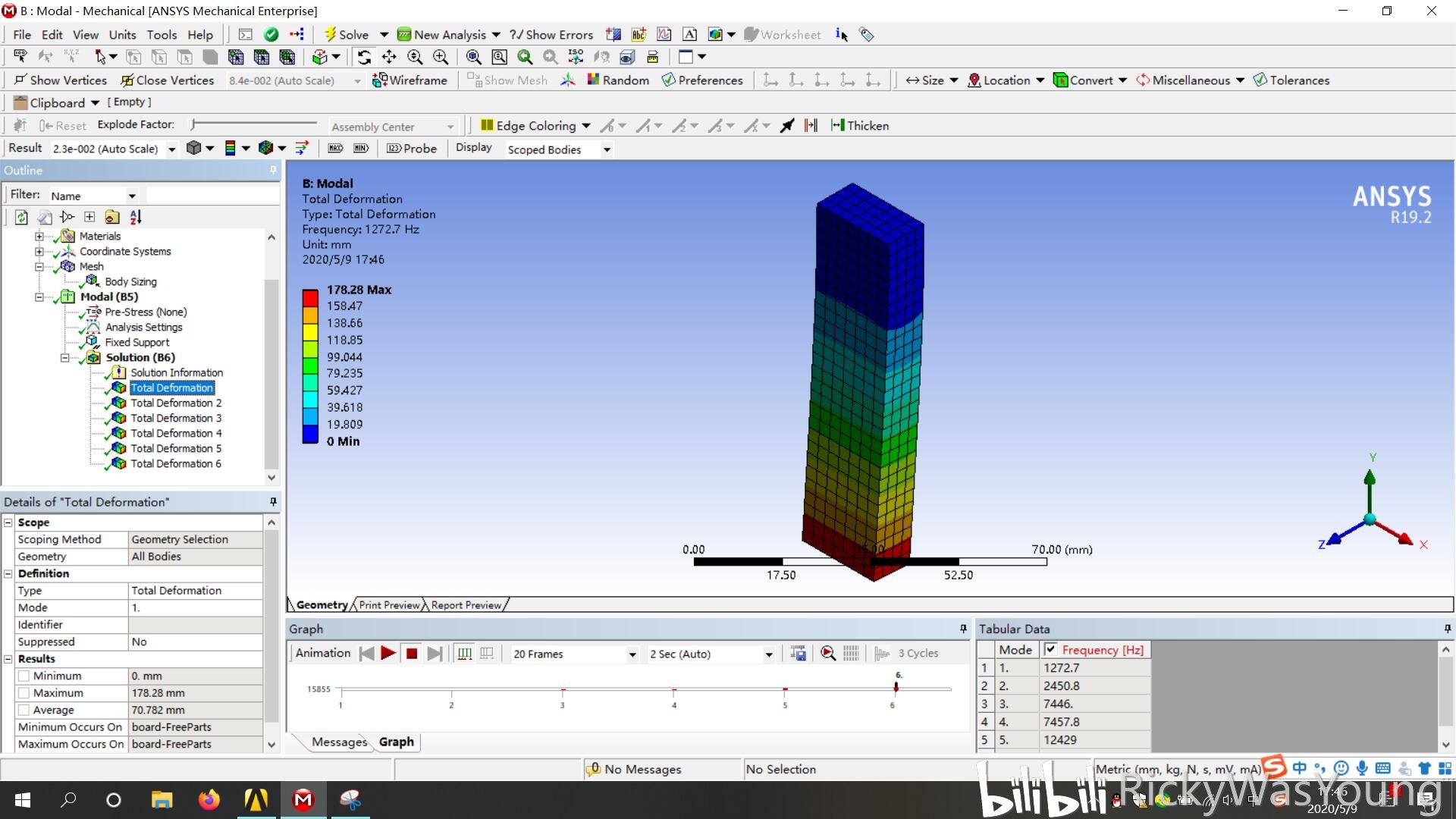
   3mm，一阶模态示意图
 

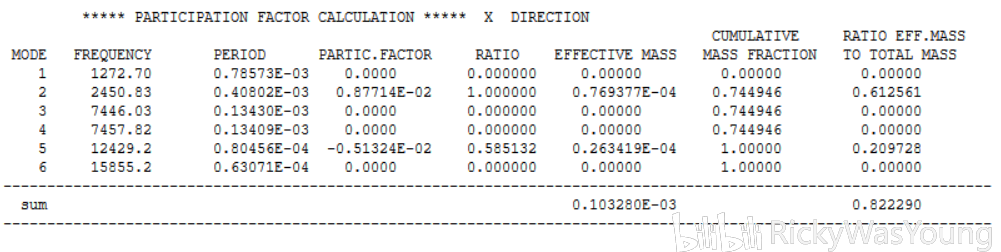
   3mm，x轴结果
 

可以看出，网格疏密对于结果有影响，不同疏密的网格对应结果也不同。一般而言，网格疏密对低阶模态影响较小，对高阶影响较大。

2.结果说明

如下图所示为element size定义为3mm时x轴的结果

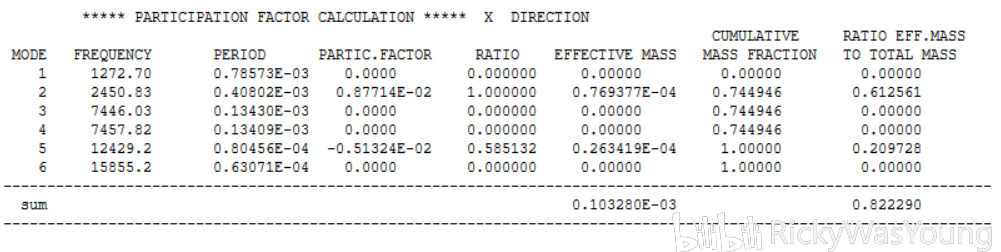
图中，MODE与FREQUENCY是阶次与该阶次对应的固有频率，PERIOD是周期（固有频率的倒数），PRACTIC.FACTOR与EFFECTIVE MASS是参与系数和有效质量（有效质量是参与系数的平方），所有有效质量的sum即为总质量（注意这里的“所有”不一定是当前阶次的总和，比如上图有6阶，但是sum可能是100阶甚至1000阶的总和），最后一项（RATIO EFF这项）是有效质量与总质量的比值，我的理解是，若该值接近于1，则说明目前所选择的阶次是合适的，即目前所选的阶次占比足够，不需要再做更高次的模态分析，反之则说明目前所选的阶次太低，还不足以完全反映模型的阶次，还需要更高阶的说明。

3.无约束的自由模态

视频中给出的是有约束的普通模态，取消掉约束则为自由模态。一般刚体的自由模态的低阶模态值都很小，因此需要多取几阶进行计算：

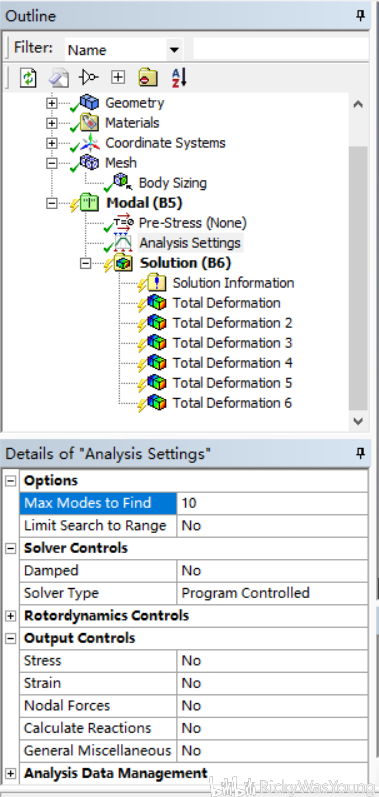
   删除约束，将模态求解设为10
 

以下是无约束自由模态的计算结果

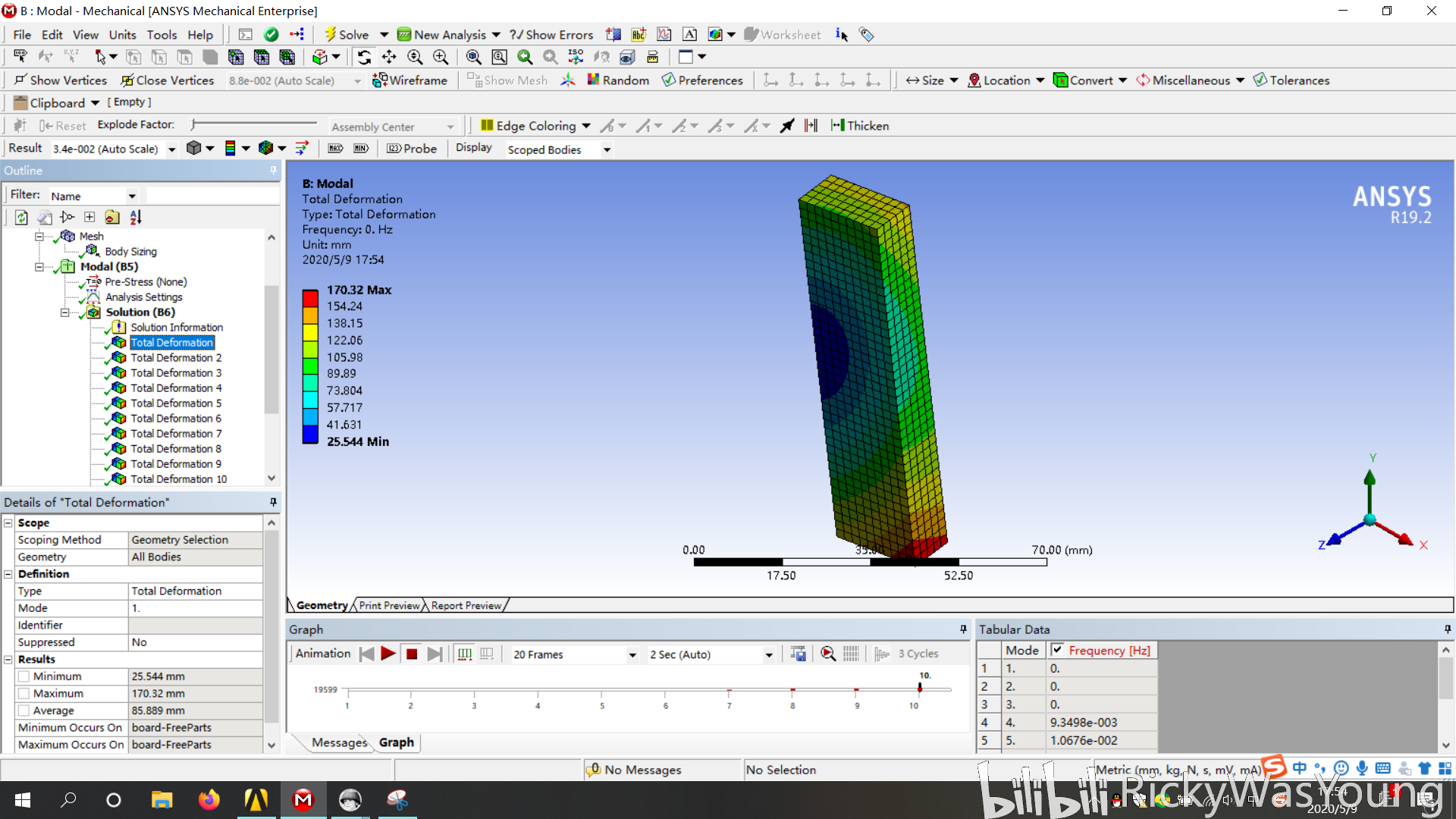
   1阶
 

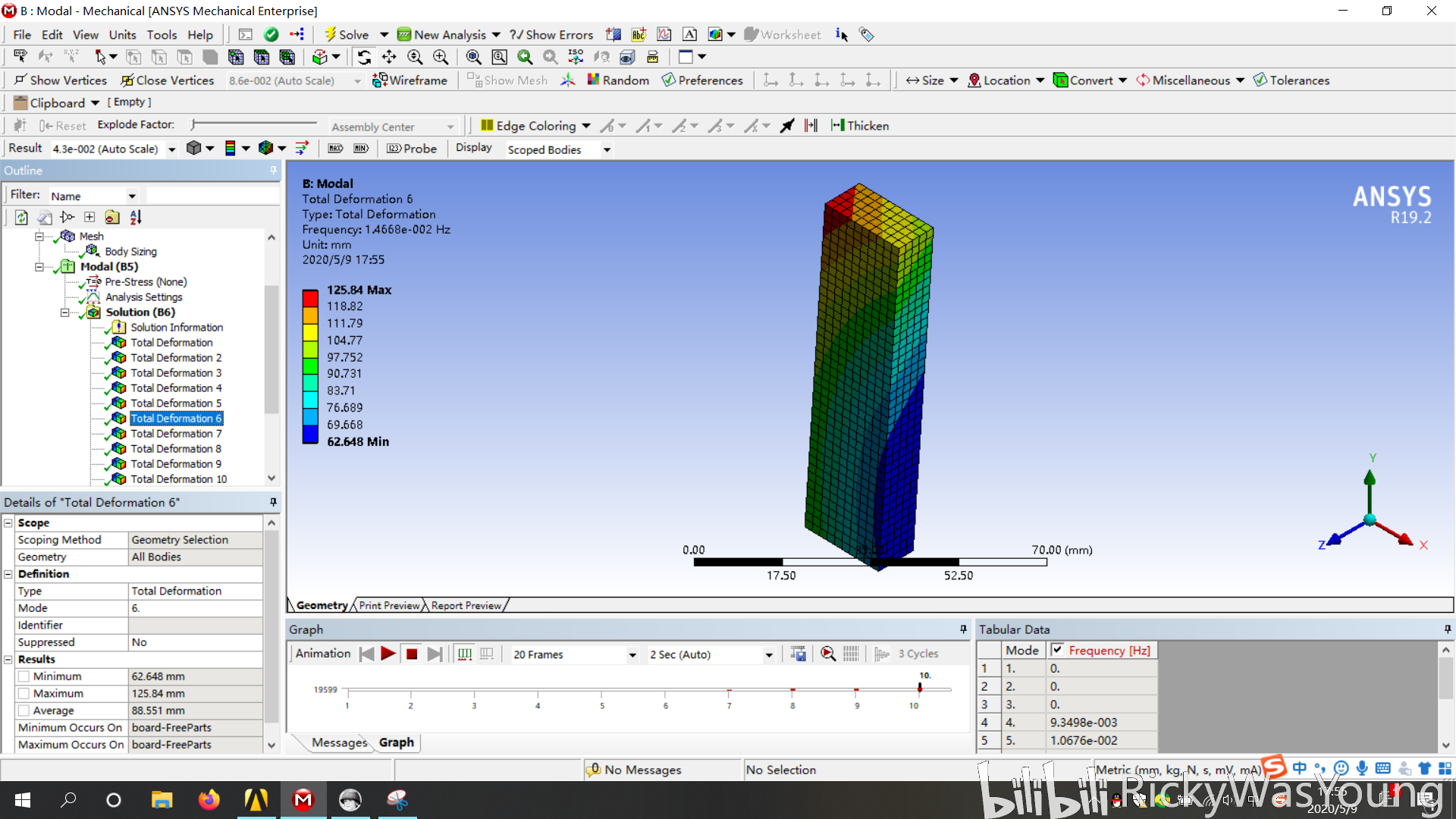
   6阶
 

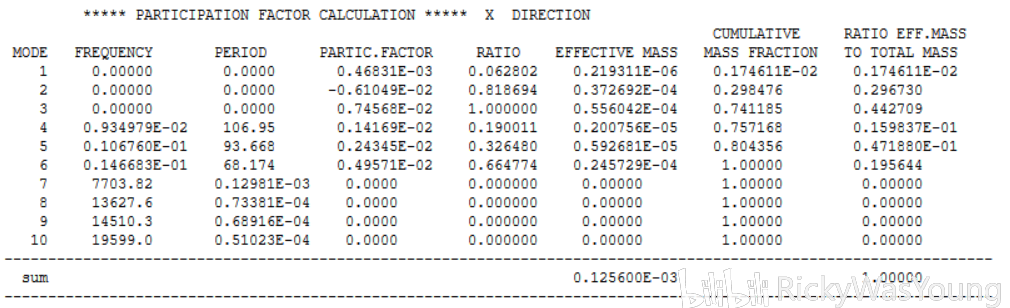
   x轴结果
 

   前五阶结果
 

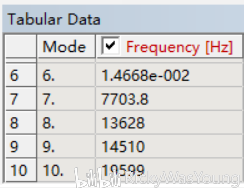
   6-10阶结果
 

可以发现，自由模态与约束模态的结果有较大差别，自由模态前6阶几乎为0，我对此的理解是，对于刚体而言，其自由度数为6，因此刚体在这六个自由度上面的运动形式表现为平移而非产生形变的振动，延伸一下观点，如果模型欠约束，则其低阶模态会产生一定的接近于0的解（这个欢迎大家验证一下）。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删