今天我来结合代码详细介绍一下如何用SciSharp STACK的TensorFlow.NET来训练一个线性回归的基本模型。线性回归模型是初入机器学习领域必修的基本模型。TensorFlow.NET为广大.NET开发者提供了一个除了ML.NET的第二个机器学习框架选择。
线性回归是一种线性方法,利用数理统计中回归分析对因变量与一个或多个独立变量之间的关系进行建模,运用十分广泛。考虑单个因变量y和单个预测变量x的情况。 自变量也称为:协变量,输入,特征; 预测变量通常称为响应,输出,结果。 我们有一组数据并符合高斯分布,假设是一个简单的线性模型。
// Prepare training Data
var train_X = np.array(3.3f, 4.4f, 5.5f, 6.71f, 6.93f, 4.168f, 9.779f, 6.182f, 7.59f, 2.167f, 7.042f, 10.791f, 5.313f, 7.997f, 5.654f, 9.27f, 3.1f);
var train_Y = np.array(1.7f, 2.76f, 2.09f, 3.19f, 1.694f, 1.573f, 3.366f, 2.596f, 2.53f, 1.221f, 2.827f, 3.465f, 1.65f, 2.904f, 2.42f, 2.94f, 1.3f);
var n_samples = train_X.shape[0];
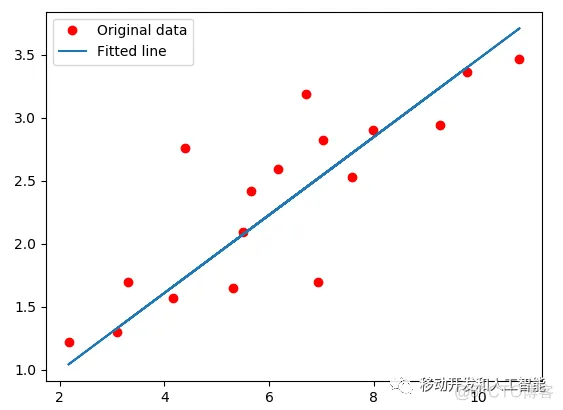
基于给定的这组数据,我们要划一根线,使这根线最接近所有的红点。这根红线可以想成一个线性的等式:y = wx + b。我们要找一组最好的w和b的值,使他的损失函数值最小,理想情况下应该是零。
损失函数帮助我们找出w和b的最佳值,这将为数据点提供最佳拟合线。由于我们找到这个w和b的最佳值,我们将此搜索问题转换为最小化问题,我们希望最小化预测值和实际值之间的误差。
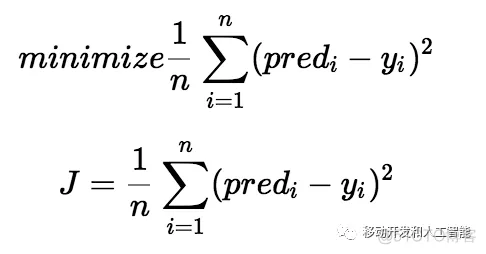
我们选择以上等式来作为最小化的损失函数。 预测值和实际值之间的差异就是误差值。 我们对所有数据点的误差求和,并将该值除以数据点的总数。 这提供了所有数据点的平均平方误差。 因此,该成本函数也称为均方误差(MSE)函数。 现在,使用此MSE函数,我们将反复更新w和b的值,使MSE值在最小值处停止迭代。
// tf Graph Input
var X = tf.placeholder(tf.float32);
var Y = tf.placeholder(tf.float32);
// Set model weights
var W = tf.Variable(rng.randn<float>(), name: "weight");
var b = tf.Variable(rng.randn<float>(), name: "bias");
// Construct a linear model
var pred = tf.add(tf.multiply(X, W), b);
// Mean squared error
var cost = tf.reduce_sum(tf.pow(pred - Y, 2.0f)) / (2.0f * n_samples);
入门机器学习需要理解的另一个重要概念是梯度下降。 梯度下降是一种更新w和b的方法,以最小化成本函数。 我们的想法是,我们从w和b的一些随机初始值开始,然后我们迭代地更改这些值以找到最小损失值。 梯度下降有助于我们了解如何更新值或下一步的方向。 梯度下降也被称为最陡下降。

举一个类比,想象一下U形的坑,你站在坑的最高点,你的目标是到达坑的底部。 有一个条件,您只能采取离散的步骤到达底部。 如果您决定一步一步,最终会到达坑的底部,但这需要更长的时间。 如果你选择每次采取更长的步骤,你会很快达到,但是,你有可能超过坑的底部,而不是完全在底部。 在梯度下降算法中,您采取的步骤数是学习率。 这决定了算法收敛到最小值的速度。
// Gradient descent
// Note, minimize() knows to modify W and b because Variable objects are trainable=True by default
var optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost);
TensorFlow.NET实例了自动梯度下降的算法。完整代码请参考Github仓库。如果我们把这个线性模型计算图用TensorBoard展现出来,就是以下这个样子: 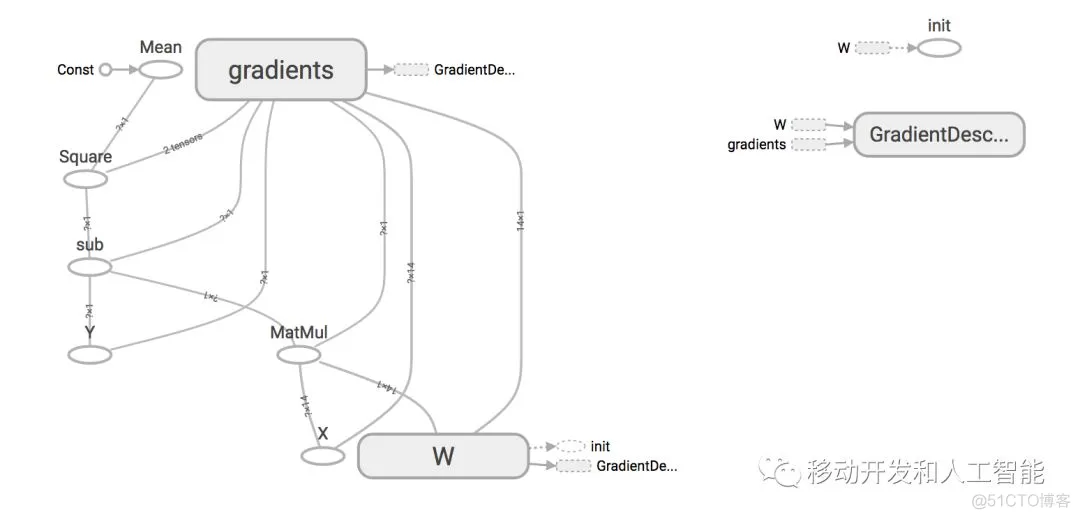
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删