机器学习实战：sklearn与TensorFlow联手

1.线性模型求解方法

闭式解（closed-form）：

直接计算参数，从而使得训练数据可以很好的满足模型。

梯度下降（gradient descent）

通过迭代方式，逐渐使得参数可以最大化的满足代价函数（cost function）。

2.线性回归计算方法

线性问题：

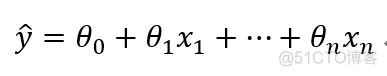
可以写成向量形式：

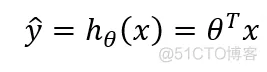
而要使求得的斯塔使得线性拟合结果最好，则需要使得RMSE（root mean square error）或者MSE（mean square error）最小，表示如下：

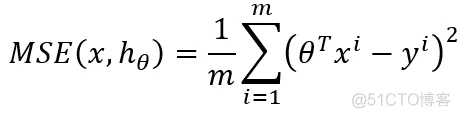
利用闭合解，容易求的解如下（具体求解过程在概率统计浙大版的书上可以查到），

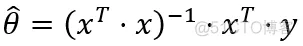
代码如下：

import numpy as np
X = 2*np.random.rand(100,1)
y = 4 + 3*X + np.random.rand(100,1)

x_b = np.c_[np.ones((100,1)),X]
theta = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)
print(theta)

如果直接使用sklearn自带的线性回归模型，则代码如下：

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X=X,y=y)
print(lr.coef_)
print(lr.intercept_)

算法复杂度，矩阵的乘法复杂度介于O（n^(2.4))到O（n^3)之间。

3.梯度下降法

基本原理：随机初始化一些theta值，然后依据局部的误差计算局部的梯度，使得theta沿着梯度反方向运动，直到梯度为0.

theta更新的计算公式为：

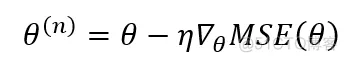
实现代码如下：

import numpy as np
eta = 0.1
LOOPNUM = 100 
m = 100

theta = np.random.rand(2,1)
for iter in range(LOOPNUM):
    gradient = 2/m*x_b.T.dot(x_b.dot(theta)-y)#梯度计算
    theta = theta - eta*gradient
print(theta)

梯度下降法的缺陷：

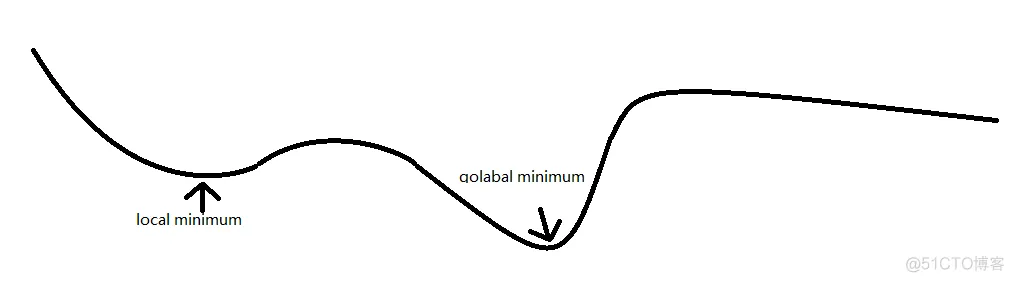
如上图所示，这条代价函数有两个极小值，其中一个是最小值，如果从左向右进行迭代，很容易陷入局部极小值，如果从右向左迭代，则需要经过很多步骤才可以找到全局最小值。

4.梯度下降法的分类

按照算法每次迭代的时候所涉及的实例数量的不同，可以分为批量梯度下降法（batch gradient descent）、随机梯度下降法（stochastic gradient descent）和小批量梯度下降法（mini-batch gradient descent）。

BGD是指每次都计算所有实例求的梯度进行计算；SGD是指每次按照随机取的一个实例计算梯度；MBGD是指

BGD

前面第3部分展示了BGD的算法

SGD

SGD每次按照随机取的一个实例计算梯度,这样可以加快计算速度，但是由于每次是随机选取的实例，因此在迭代过程中，虽然会不断趋近代价函数的全局最小值，但是有可能在最小值附近一直震荡，但是由于每次迭代都有随机性，因此SGD比BGD更容易跳出局部最优值。因此SGD的优点是容易逃离局部最优值，缺点是不太容易获得最优值而是获得次优值。解决上述问题的一个可行方法可以初始迭代速率大一些，逐步缩小迭代速率（模拟退火），这一系列的学习速率被称之为学习计划；

代码如下：

import numpy as ny
t0 , t1 = 5 ,50
LOOPNUM = 100 
m = 100

def learnScheduel(r):
    return t0/(t1+r)

theta = np.random.rand(2,1)

for iter in range(LOOPNUM):
    randNum = np.random.randint(m)
    x_b_r = x_b[randNum:randNum+1]
    y_r = y[randNum:randNum+1]
    
    gradient = 2*x_b_r.T.dot(x_b_r.dot(theta) - y_r)#梯度计算
    eta = learnScheduel( iter )
    theta = theta - eta*gradient
print(theta)

MBGD（mini-batch Grandient Descent）

与BGD和SGD不同，MBGD既不是每次迭代都使用所有实例去计算，也不是只是用单个实例去计算，而是随机取小批量实例去计算。比起SGD，MBGD在最优值的逼近方面更容易逼近最优值，然而却更不容易逃离出局部最优值。

5.多项式回归

利用线性回归的一个假设是如解释变量和被解释变量之间是线性关系，而如果真实的数据之间存在的并不是线性关系，比如是抛物线形状的关系，要怎么处理。这个时候，就可以采用多项式回归去拟合。多项式回归，顾名思义，就是对那些被解释变量和解释变量之间存在多项式关系的实例进行拟合。操作过程也简单粗暴，假设存在一个线性模型，其右侧可以表示为X+2，现在有新的情况是需要拟合结果X^2+X+3，那么就先扩展原来的解释变量成（X、X^2),然后进行线性拟合。

代码如下：

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from  sklearn.linear_model import LinearRegression
m = 100

X = 6*np.random.rand(m,1) - 3
y = 0.5*X**2 + 12*X+ 2 + np.random.randn(m,1)

polyFeatures = PolynomialFeatures(degree = 2,include_bias=False)
XPly = polyFeatures.fit_transform(X)

lnReg = LinearRegression()
lnReg.fit(X = XPly,y = y)
print( lnReg.intercept_ )
print( lnReg.coef_ )

打印结果：

[1.80772977]
[[11.91640908  0.56508895]]
从结果看出，最终拟合效果是：常数项拟合结果是1.80（实际是2），一次项拟合结果是11.91（实际是12），
二次项拟合结果是0.56（实际是0.5）



6.学习曲线

如果线性回归无法很好拟合实例，那么可以利用二次元去拟合，如果效果不好，还可以用三次、四次...、100次，
这个时候很可能就可以非常好的拟合实例，甚至基本上和实例是一致的，但是，这个时候去测试的时候效果可能就不理想，因为
过拟合了。那么如何消除过拟合呢，常用的方法就是观察模型在训练数据和测试数据上面的表现，如果在训练数据上面的拟合效
果很好，但是在测试集上面的效果不好，那么就是过拟合了，如果在训练数据和测试数据上面的效果都不好，那么就是拟合不足了。

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
%matplotlib inline
def plot_learning_curves(model,X,y,ratio):
    X_train,X_val,y_train,y_val = train_test_split(X,y,test_size=ratio)
    train_errors,val_errors = [],[]
    for m in range(1,len(X_train)):
        model.fit(X_train[:m],y[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_val)
        train_errors.append(mean_squared_error(y_train_predict,y_train[:m]))
        val_errors.append(mean_squared_error(y_val_predict,y_val))
    plt.plot(np.sqrt(train_errors),'r--+',linewidth = 2,label = 'train')
    plt.plot(np.sqrt(val_errors),'b-',linewidth = 2,label = 'val')

lnReg = LinearRegression()
plot_learning_curves(model=lnReg,X=XPly,y=y,ratio=0.2)

输出图片如下：

由于上面的实例简单，大概到5个实例的时候，训练效果就很明显了，这个时候训练的RMSE和测试的RMSE就很接近了。

6.线性模型正规化

为了防止过拟合，一个好的办法就是对模型做正规化。对多项式回归的正规化可以是降低维度，对线性模型的约束就是对其权重矩阵的约束，下面分别通过三种方式进行约束，对应模型是岭回归（Ridge Regression）、Lasso回归、弹性网络（Elastic Net）。

岭回归
代价函数：

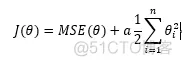
theata的估计：

代码：

from sklearn.linear_model import Ridge
ridgClf = Ridge()
ridgClf.fit(X=X,y=y)
print('coef==%f'%ridgClf.coef_)
print('intercept==%f'%ridgClf.intercept_)

Lasso 回归（Least Absolute Shrinkage and Selection Operator Regression）

代价函数：

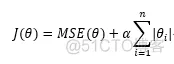
代码：

from sklearn.linear_model import Lasso
ridgClf = Lasso(alpha = 0.1)
ridgClf.fit(X=X,y=y)
print('coef==%f'%ridgClf.coef_)
print('intercept==%f'%ridgClf.intercept_)

弹性网络

代价函数：

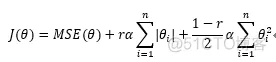
代码：

from sklearn.linear_model import ElasticNet
ridgClf = ElasticNet(alpha = 0.1,l1_ratio=0.5)
ridgClf.fit(X=X,y=y)
print('coef==%f'%ridgClf.coef_)
print('intercept==%f'%ridgClf.intercept_)

7.提前结束（Early Stopping）

还有一个正规化学习算法的方式，比如在GD迭代过程中，可以在验证错误达到最小值的时候就立即结束，这被称为提前结束。如下图所示，随着迭代次数的增加，训练的RMSE和验证的RMSE都会在开始的时候下降，当下降到一定程度的时候，验证的RMSE就开始反弹，这说明开始出现过拟合现象了，那么在验证RMSE反弹之前就停止就是一个好的办法，可以找到最优模型。

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2)
sgd_reg = SGDRegressor(n_iter=1,warm_start=True,penalty=None,learning_rate="constant",
eta0=0.0005)minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train,y_train)
y_val_predict = sgd_reg.predict(X_test)
val_error = mean_squared_error(y_val_predict,y_test)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
        
        

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删