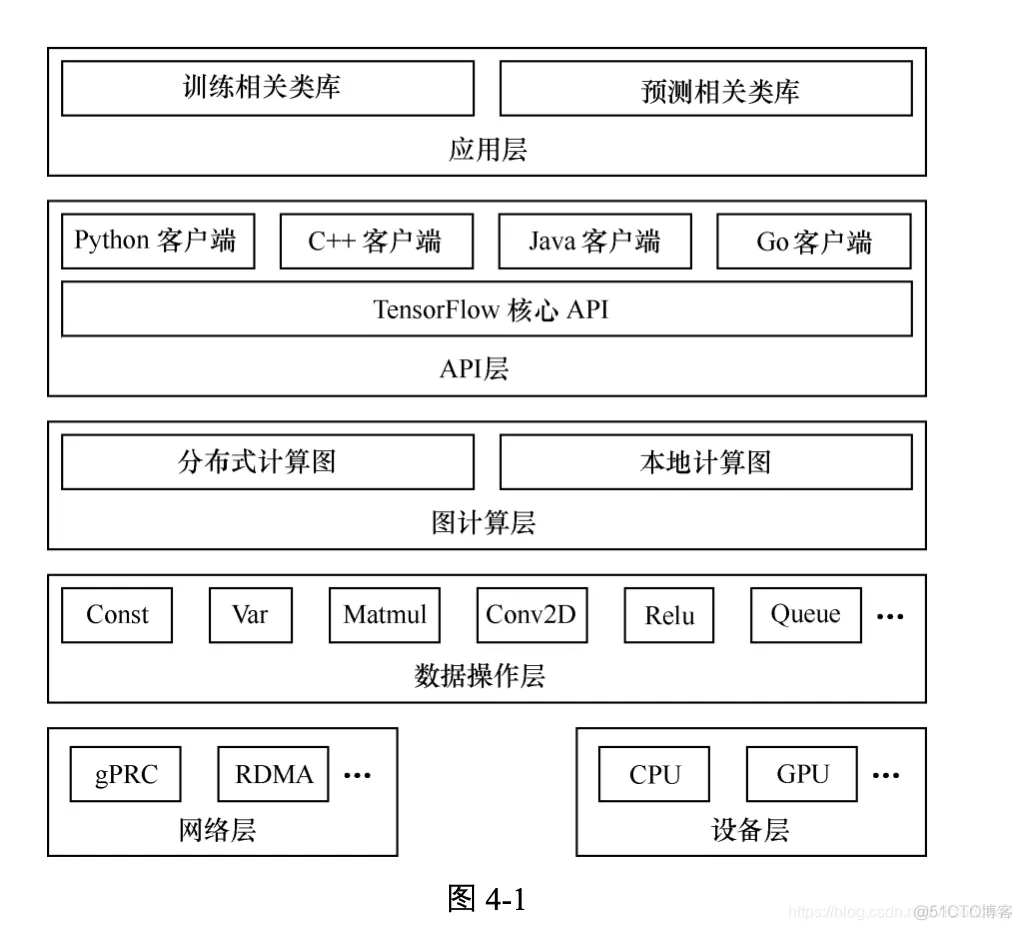
图 4-1 给出的是 TensorFlow 的系统架构,自底向上分为设备层和网络层、数据操作层、 图计算层、API 层、应用层,其中设备层和网络层、数据操作层、图计算层是 TensorFlow 的核心层。
TensorFlow 的设计理念主要体现在以下两个方面。
1)将图的定义和图的运行完全分开。
因此,TensorFlow 被认为是一个“符号主义”的库。
现有的深度学习框架中,Torch 是典型的命令式的,Caffe、MXNet 采用了两种编程模式混合的方法,而 TensorFlow 完全采用符号式编程
符号式计算一般是先定义各种变量,然后建立一个数据流图,在数据流图中规定各个变量之间的计算关系,最后需要对数据流图进行编译,但此时的数据流图还是一个空壳儿,里面没有任何实际数据,只有把需要运算的输入放进去后,才能在整个模型中形成数据流,从而形成输出值。 例如:
t=8+9 print(t)
在传统的程序操作中,定义了 t 的运算,在运行时就执行了,并输出 17。
而在 TensorFlow
中,数据流图中的节点,实际上对应的是 TensorFlow API 中的一个操作,
并没有真正去运行:
import tensorflow as tf
t = tf.add(8, 9)
print(t) # 输出 Tensor("Add_1:0", shape=(), dtype=int32)
定义了一个操作,但实际上并没有运行。
2)TensorFlow 中涉及的运算都要放在图中,而图的运行只发生在会话(session)中。开 启会话后,就可以用数据去填充节点,进行运算;关闭会话后,就不能进行计算了。因此,会 话提供了操作运行和 Tensor 求值的环境。例如:
import tensorflow as tf
##### 创建图
a = tf.constant([1.0, 2.0]) b = tf.constant([3.0, 4.0]) c=a*b
#### 创建会话
sess = tf.Session()
#### 计算c
print sess.run(c) # 进行矩阵乘法,输出[3., 8.] sess.close()
了解了设计理念,接下来看一下 TensorFlow 的编程模型。
TensorFlow 是用数据流图做计算的,因此我们先创建一个数据流图(也称为网络结构图), 如图 4-2 所示,看一下数据流图中的各个要素。
图 4-2 讲述了 TensorFlow 的运行原理。图中包含输入(input)、塑形(reshape)、Relu 层(Relu layer)、Logit 层(Logit layer)、Softmax、交叉熵(cross entropy)、梯度(gradient)、SGD 训练
(SGD Trainer)等部分,是一个简单的回归模型。
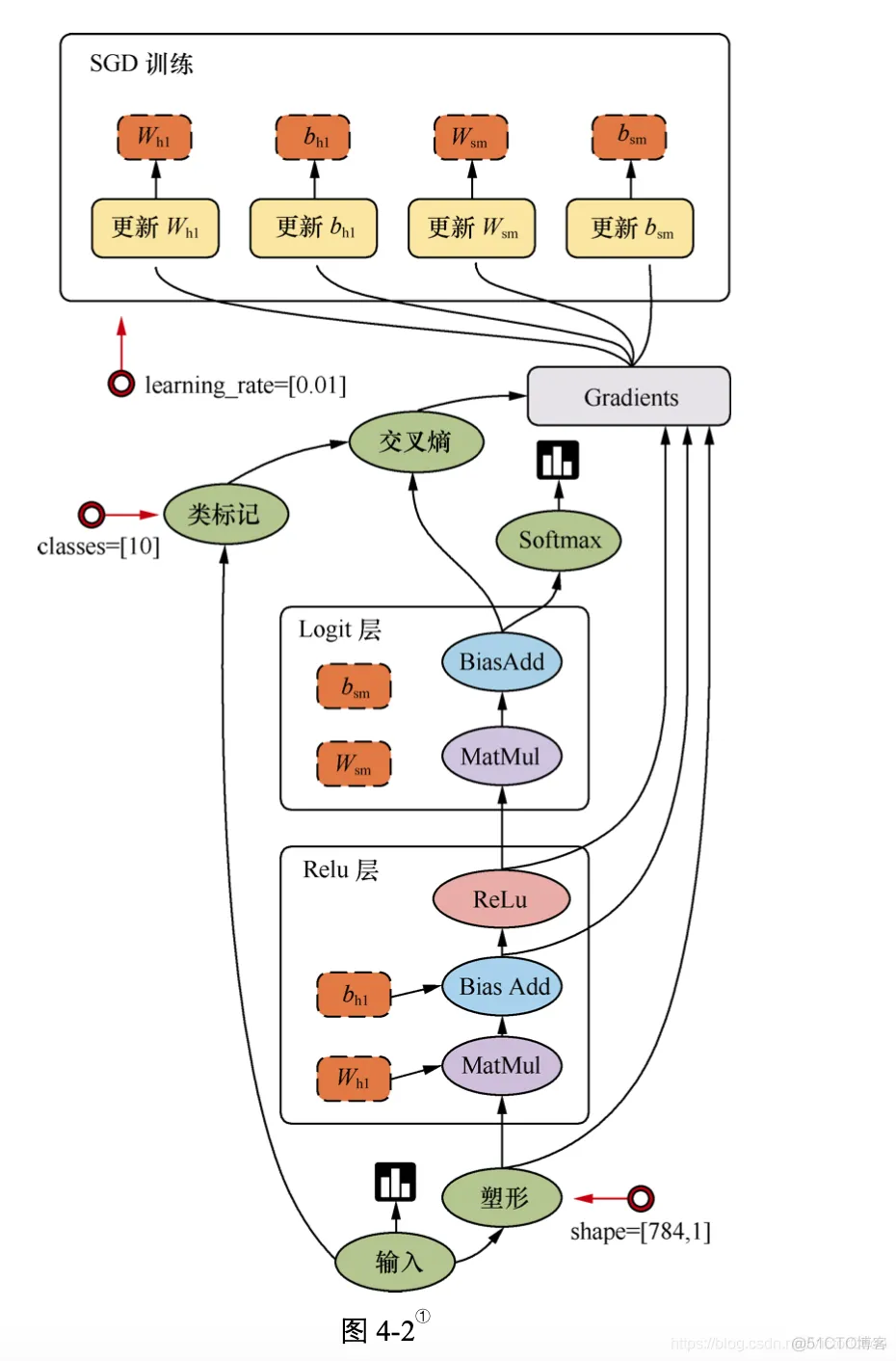
它的计算过程是,首先从输入开始,经过塑形后,一层一层进行前向传播运算。Relu 层(隐 藏层)里会有两个参数,即Wh1和bh1,在输出前使用ReLu(Rectified Linear Units)激活函数 做非线性处理。然后进入 Logit 层(输出层),学习两个参数 Wsm 和 bsm。用 Softmax 来计算输出结果中各个类别的概率分布。用交叉熵来度量两个概率分布(源样本的概率分布和输出结果 的概率分布)之间的相似性。然后开始计算梯度,这里是需要参数 Wh1、bh1、Wsm 和 bsm,以及 交叉熵后的结果。随后进入 SGD 训练,也就是反向传播的过程,从上往下计算每一层的参数, 依次进行更新。也就是说,计算和更新的顺序为 bsm、Wsm、bh1 和 Wh1。
TensorFlow 的边有两种连接关系:数据依赖和控制依赖 。
其中,实线边表示数据依赖,代表数据,即张量。
任意维度的数据统称为张量。在机器学习算法中,张量在数据流图中从前 往后流动一遍就完成了一次前向传播(forword propagation),而残差2从后向前流动一遍就完成 了一次反向传播(backword propagation)。
还有一种特殊边,一般画为虚线边,称为控制依赖(control dependency),可以用于控制操 作的运行,这被用来确保 happens-before 关系,这类边上没有数据流过,但源节点必须在目的 节点开始执行前完成执行。常用代码如下:
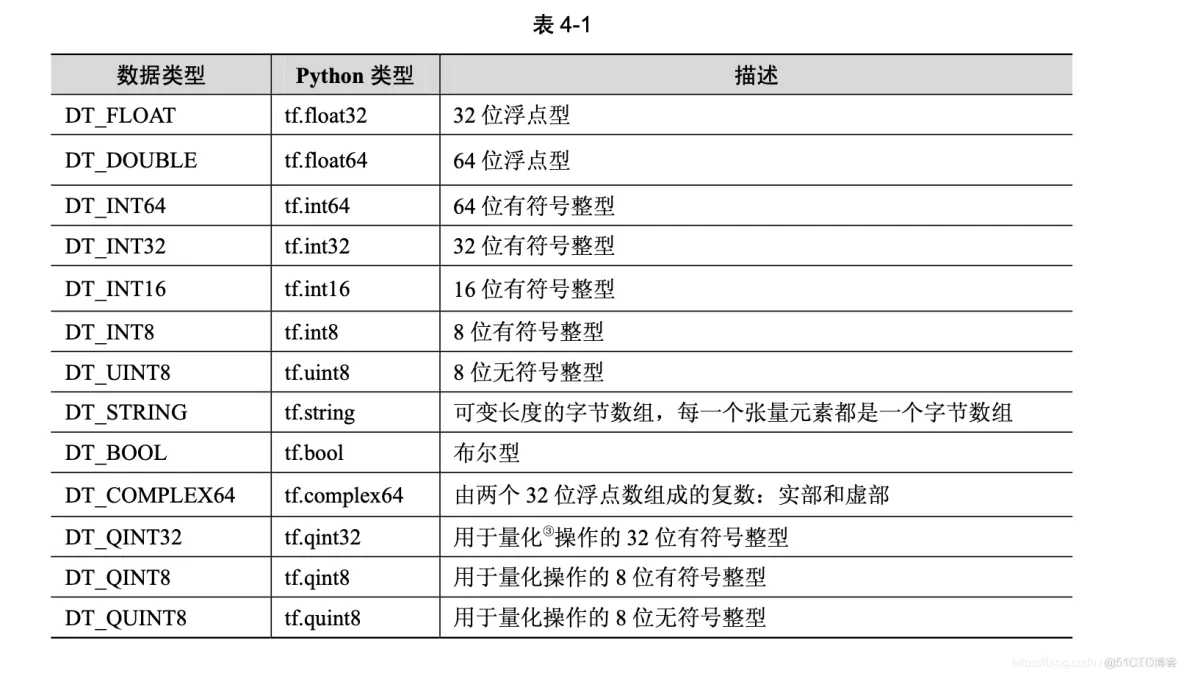
tf.Graph.control_dependencies(control_inputs) TensorFlow 支持的张量具有表 4-1 所示的数据属性。
图中的节点又称为算子,它代表一个操作(operation,OP),一般用来表示施加的数学运 算,也可以表示数据输入(feed in)的起点以及输出(push out)的终点,或者是读取/写入持久 变量(persistent variable)的终点。表 4-2 列举了一些 TensorFlow 实现的算子。算子支持表 4-1 所示的张量的各种数据属性,并且需要在建立图的时候确定下来。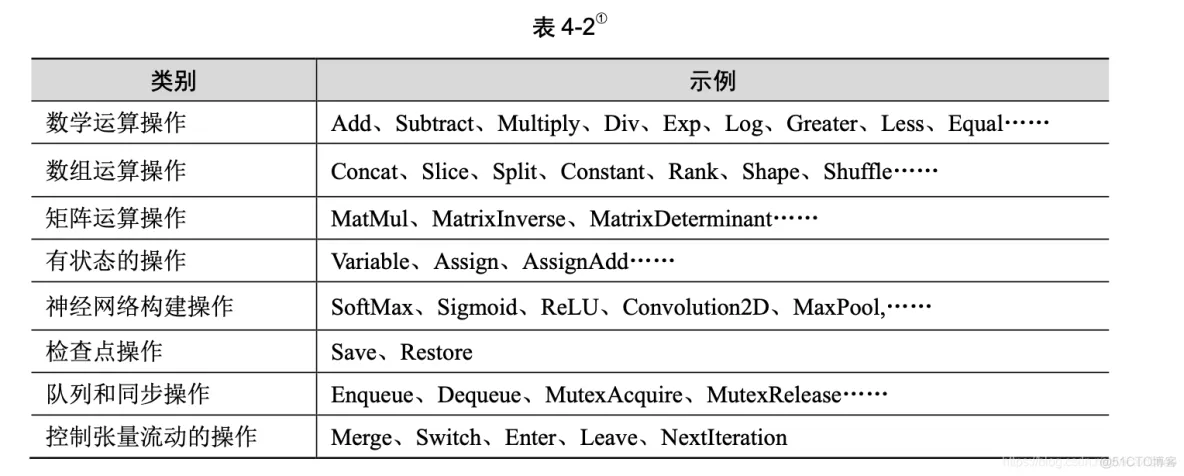
除了边和节点,TensorFlow 还涉及其他一些概念,如图、会话、设备、变量、内核等。
1.图
把操作任务描述成有向无环图。那么,如何构建一个图呢?构建图的
第一步是创建各个节点。具体如下:
import tensorflow as tf
# 创建一个常量运算操作,产生一个 1×2 矩阵
matrix1 = tf.constant([[3., 3.]])
# 创建另外一个常量运算操作,产生一个 2×1 矩阵
matrix2 = tf.constant([[2.],[2.]])
# 创建一个矩阵乘法运算 ,把 matrix1 和 matrix2 作为输入
# 返回值 product 代表矩阵乘法的结果
product = tf.matmul(matrix1, matrix2)
启动图的第一步是创建一个 Session 对象。会话(session)提供在图中执行操作的一些方法。 一般的模式是,建立会话,此时会生成一张空图,在会话中添加节点和边,形成一张图,然后 执行。
要创建一张图并运行操作的类,在 Python 的 API 中使用 tf.Session,在 C++ 的 API 中使用 tensorflow::Session。示例如下:
with tf.Session() as sess:
result = sess.run([product])
print result
在调用 Session 对象的 run()方法来执行图时,传入一些 Tensor,这个过程叫填充(feed); 返回的结果类型根据输入的类型而定,这个过程叫取(fetch)。
与会话相关的源代码位于 tensorflow-1.1.0/tensorflow/python/client/session.py。
会话是图交互的一个桥梁,一个会话可以有多个图,会话可以修改图的结构,也可以往图 中注入数据进行计算。因此,会话主要有两个 API 接口:Extend 和 Run。Extend 操作是在 Graph 中添加节点和边,Run 操作是输入计算的节点和填充必要的数据后,进行运算,并输出运算 结果。
设备(device)是指一块可以用来运算并且拥有自己的地址空间的硬件,如 GPU 和 CPU。
TensorFlow 为了实现分布式执行操作,充分利用计算资源,
可以明确指定操作在哪个设备上执行。具体如下:
with tf.Session() as sess:
# 指定在第二个 gpu 上运行
with tf.device("/gpu:1"):
matrix1 = tf.constant([[3., 3.]])
matrix2 = tf.constant([[2.],[2.]])
product = tf.matmul(matrix1, matrix2)
与设备相关的源代码位于 tensorflow-1.1.0/tensorflow/python/framework/device.py。
变量(variable)是一种特殊的数据,它在图中有固定的位置,不像普通张量那样可以流动。 例如,创建一个变量张量,使用 tf.Variable()构造函数,这个构造函数需要一个初始值,初始值 的形状和类型决定了这个变量的形状和类型:
# 创建一个变量,初始化为标量 0
state = tf.Variable(0, name="counter")
创建一个常量张量:
input1 = tf.constant(3.0)
TensorFlow 还提供了填充机制,可以在构建图时使用 tf.placeholder()临时替代任意操作的张 量,在调用 Session 对象的 run()方法去执行图时,使用填充数据作为调用的参数,调用结束后, 填充数据就消失。代码示例如下:
input1 = tf.placeholder(tf.float32)
input2 = tf.placeholder(tf.float32)
output = tf.multiply(input1, input2)
with tf.Session() as sess:
print sess.run([output],
feed_dict={input1:[7.], input2:[2.]})
# 输出 [array([ 14.], dtype=float32)]
我们知道操作(operation)是对抽象操作(如 matmul 或者 add)的一个统称,而内核(kernel) 则是能够运行在特定设备(如 CPU、GPU)上的一种对操作的实现。因此,同一个操作可能会 对应多个内核。
当自定义一个操作时,需要把新操作和内核通过注册的方式添加到系统中。
这里主要介绍基于 Python 的 API,基于其他语言的 API 也大同小异
TensorFlow 的计算表现为数据流图,所以 tf.Graph 类中包含一系列表示计算的操作对象 (tf.Operation),以及在操作之间流动的数据— 张量对象(tf.Tensor)。与图相关的 API 均位于要的是理解 API 的功能及其背后的原理。 4.4.1 图、操作和张量tf.Graph 类中,参见表 4-3。
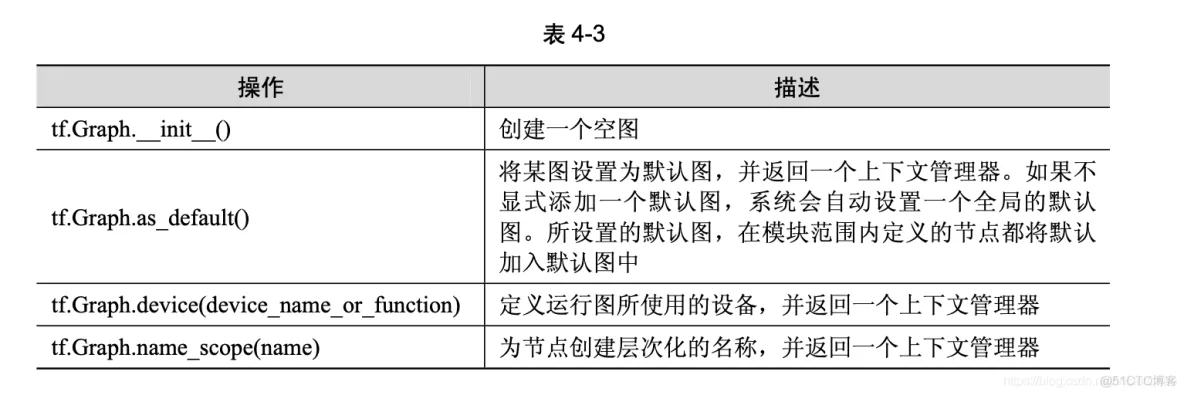
tf.Operation 类代表图中的一个节点,用于计算张量数据。该类型由节点构造器(如 tf.matmul() 或者 Graph.create_op())产生。例如,c = tf.matmul(a, b)创建一个 Operation 类,其类型为 MatMul 的操作类。与操作相关的 API 均位于 tf.Operation 类中,参见表 4-4。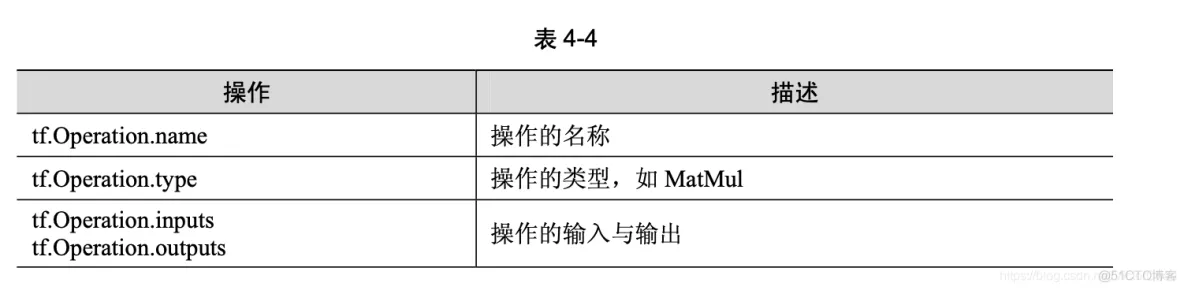

tf.Tensor 类是操作输出的符号句柄,它不包含操作输出的值,而是提供了一种在 tf.Session 中计算这些值的方法。这样就可以在操作之间构建一个数据流连接,使 TensorFlow 能够执行一 个表示大量多步计算的图形。与张量相关的 API 均位于 tf.Tensor 类中,参见表 4-5。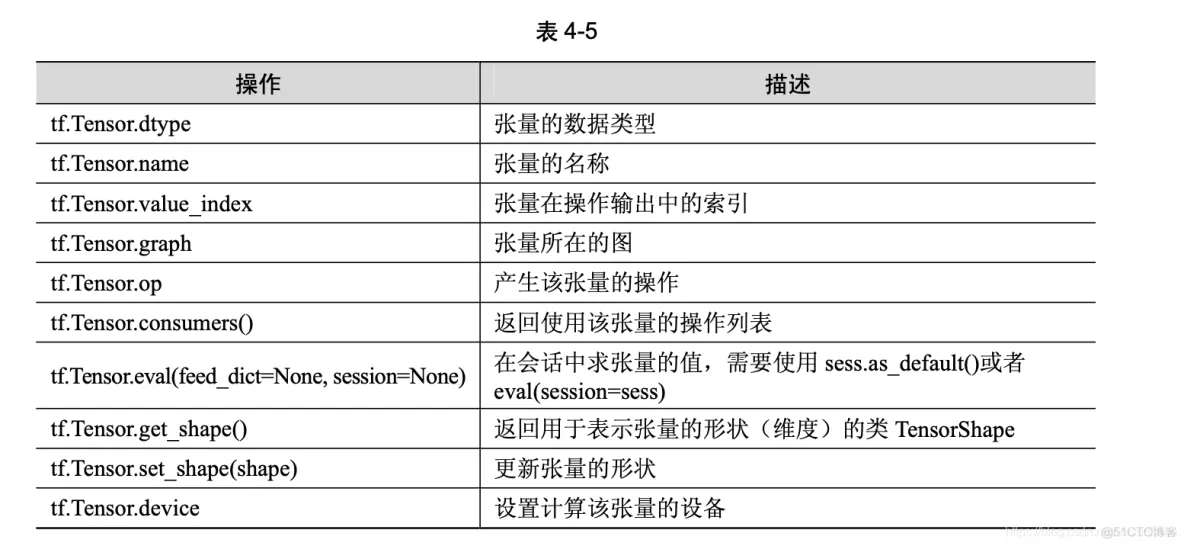
可视化时,需要在程序中给必要的节点添加摘要(summary),摘要会收集该节点的数据,并标记上第几步、时 间戳等标识,写入事件文件(event file)中。tf.summary.FileWriter 类用于在目录中创建事件文件, 并且向文件中添加摘要和事件,用来在 TensorBoard 中展示。9.3 节将详细讲解可视化的过程。
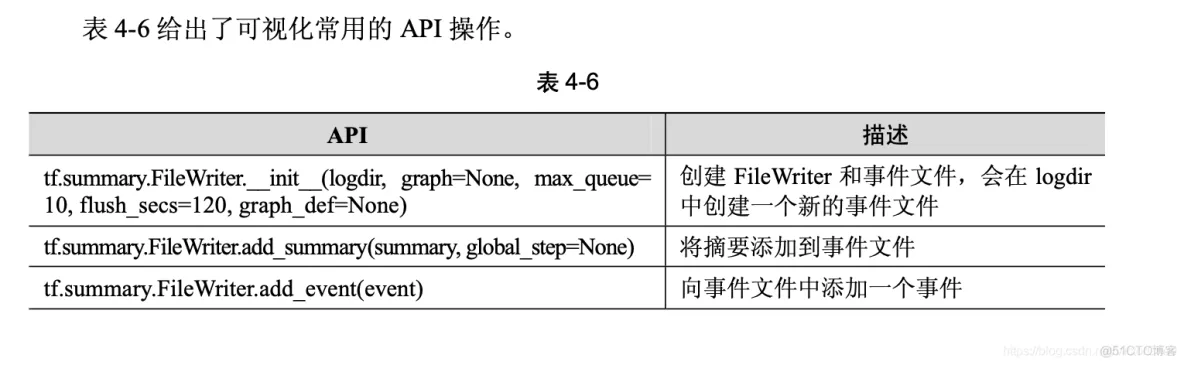
在 TensorFlow 中有两个作用域(scope),一个是 name_scope,另一个是 variable_scope。





批标准化一般用在非线性映射(激活函数)之前,对 x=Wu+b 做规范化,使结果(输出 信号各个维度)的均值为 0,方差为 1。让每一层的输入有一个稳定的分布会有利于网络的 训练。
批标准化通过规范化让激活函数分布在线性区间,结果就是加大了梯度,让模型更加大胆地进行梯度下降,于是有如下优点:
● 加大探索的步长,加快收敛的速度;
● 更容易跳出局部最小值
● 破坏原来的数据分布,一定程度上缓和过拟合
因此,在遇到神经网络收敛速度很慢或梯度爆炸(gradient explode)等无法训练的情况下, 都可以尝试用批标准化来解决。
我们对每层的 Wx_plus_b 进行批标准化,这个步骤放在激活函数之前:
# 计算 Wx_plus_b 的均值和方差,其中 axes=[0]表示想要标准化的维度
fc_mean, fc_var = tf.nn.moments(Wx_plus_b, axes=[0], )
scale = tf.Variable(tf.ones([out_size]))
shift = tf.Variable(tf.zeros([out_size]))
epsilon = 0.001
Wx_plus_b = tf.nn.batch_normalization(Wx_plus_b,
fc_mean, fc_var, shift,scale, epsilon)
# Wx_plus_b = (Wx_plus_b - fc_mean) / tf.sqrt(fc_var + 0.001)
# 也就是在做:
# Wx_plus_b = Wx_plus_b * scale + shift
本节主要介绍 TensorFlow 中构建神经网络所需的神经元函数,包括各种激活函数、卷积函 数、池化函数、损失函数、优化器等。读者阅读时,务必把本节介绍的常用 API 记熟,这有利 于在“实战篇”轻轻松松地构建神经网络进行训练。
激活函数(activation function)运行时激活神经网络中某一部分神经元,将激活信息向后 传入下一层的神经网络。神经网络之所以能解决非线性问题(如语音、图像识别),本质上就 是激活函数加入了非线性因素,弥补了线性模型的表达力,把“激活的神经元的特征”通过函 数保留并映射到下一层。
因为神经网络的数学基础是处处可微的,所以选取的激活函数要能保证数据输入与输出也是可微的。那么激活函数在 TensorFlow 中是如何表达的呢?
激活函数不会更改输入数据的维度,也就是输入和输出的维度是相同的。TensorFlow 中有 如下激活函数,它们定义在 tensorflow-1.1.0/tensorflow/python/ops/nn.py 文件中,这里包括平滑 非线性的激活函数,如 sigmoid、tanh、elu、softplus 和 softsign,也包括连续但不是处处可微的 函数 relu、relu6、crelu 和 relu_x,以及随机正则化函数 dropout:
tf.nn.relu()
tf.nn.sigmoid()
tf.nn.tanh()
tf.nn.elu()
tf.nn.bias_add()
tf.nn.crelu()
tf.nn.relu6()
tf.nn.softplus()
tf.nn.softsign()
tf.nn.dropout() # 防止过拟合,用来舍弃某些神经元
上述激活函数的输入均为要计算的 x(一个张量),输出均为与 x 数据类型相同的张量。常 见的激活函数有 sigmoid、tanh、relu 和 softplus 这 4 种。下面我们就来逐一讲解。
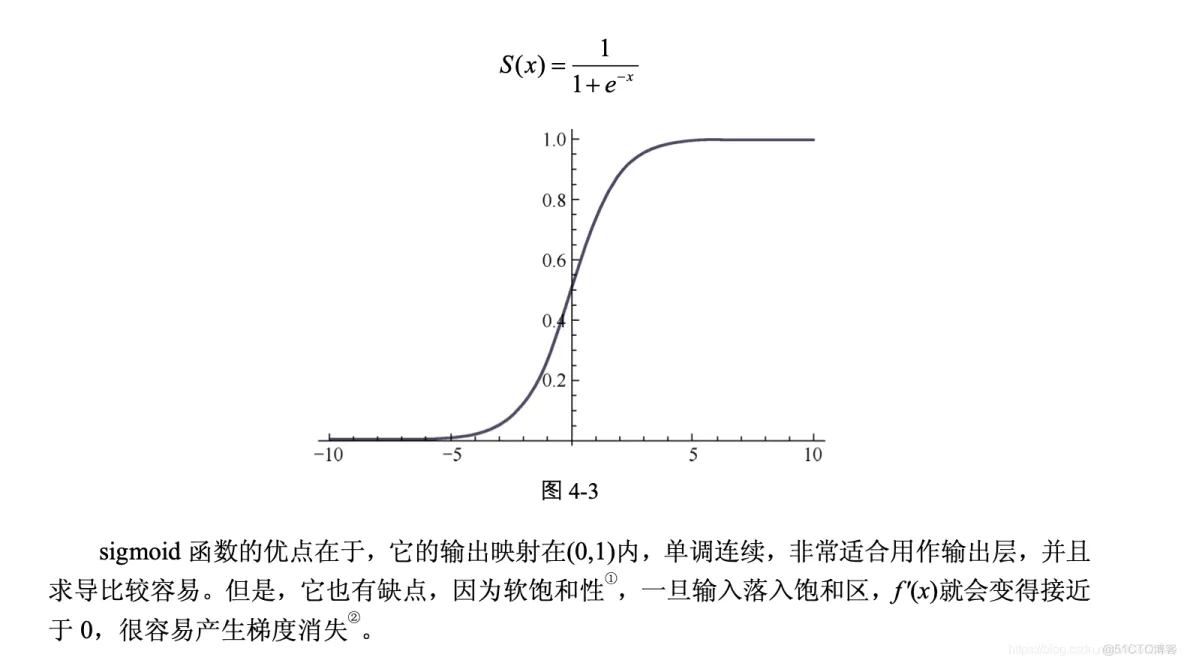
(1)sigmoid 函数。
这是传统神经网络中最常用的激活函数之一(另一个是 tanh),对应的 公式和图像如图 4-3 所示。
使用方法如下:
a = tf.constant([[1.0, 2.0], [1.0, 2.0], [1.0, 2.0]])
sess = tf.Session()
print sess.run(tf.sigmoid(a))
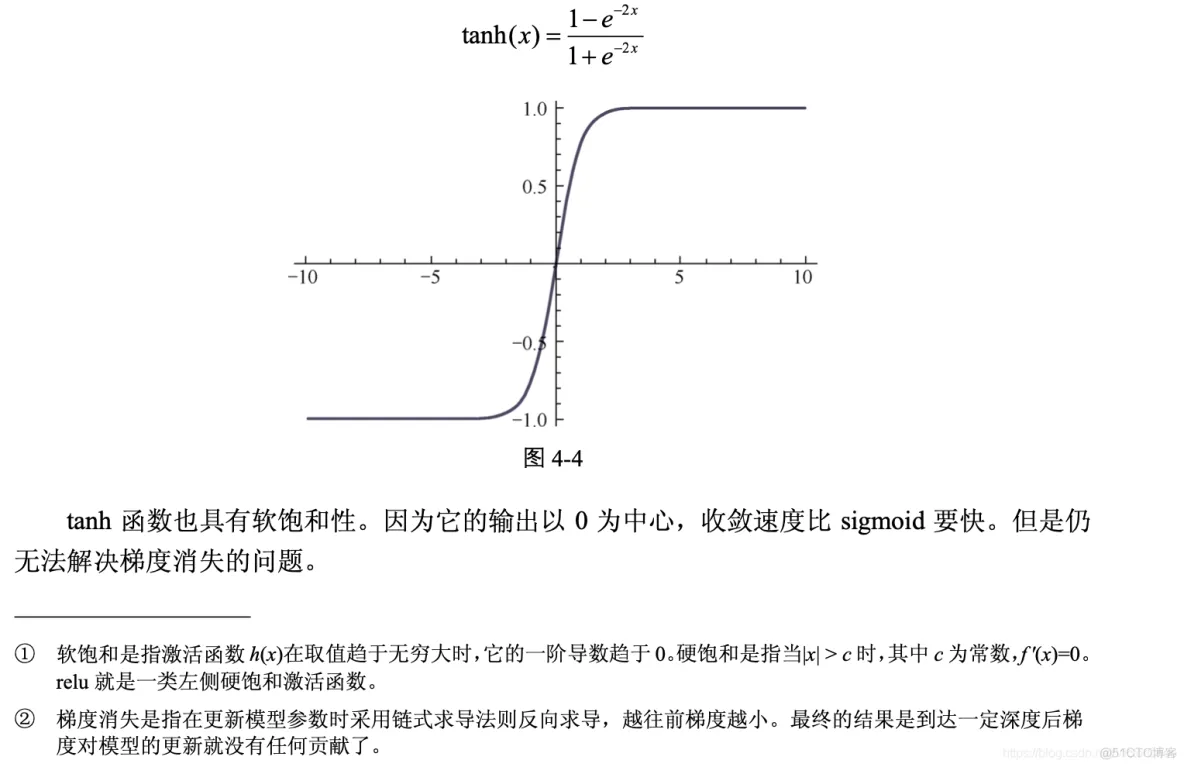
(2)tanh 函数。对应的公式和图像如图 4-4 所示。
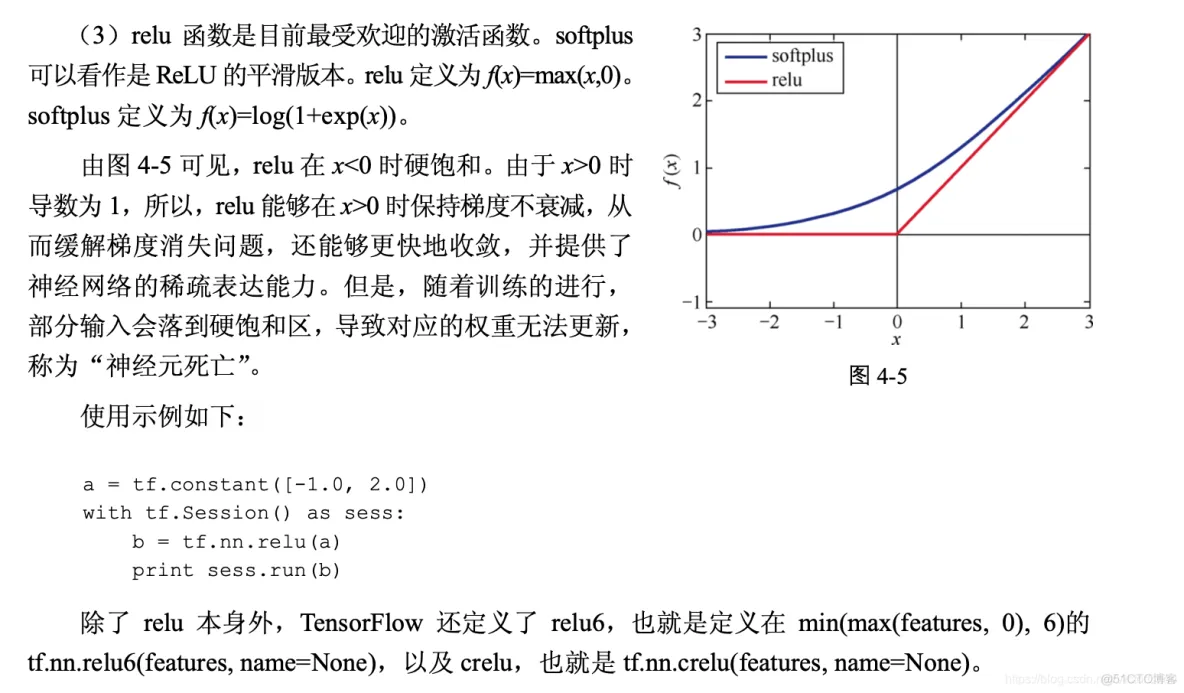

卷积函数是构建神经网络的重要支架,是在一批图像上扫描的二维过滤器
(1)tf.nn.convolution(input, filter, padding, strides=None,
dilation_rate=None, name=None, data_format =None)
#这个函数计算 N 维卷积的和。
(2)tf.nn.conv2d(input, filter, strides, padding,
use_cudnn_on_gpu=None, data_format=None, name=None)
#这个函数的作用是对一个四维的输入数据 input 和四维的卷积核 filter
#进行操作,然后对输入数据进行一个二维的卷积操作,最后得到卷积之后的结果。
def conv2d(input, filter, strides, padding,
use_cudnn_on_gpu=None, data_format=None, name=None)
# 输入:
# input:一个 Tensor。数据类型必须是 float32 或者 float64
# filter:一个 Tensor。数据类型必须是 input 相同
# strides:一个长度是 4 的一维整数类型数组,
#每一维度对应的是 input 中每一维的对应移动步数,
# 比如,strides[1]对应 input[1]的移动步数
# padding:一个字符串,取值为 SAME 或者 VALID
# padding='SAME':仅适用于全尺寸操作,即输入数据维度和输出数据维度相同
# padding='VALID:适用于部分窗口,即输入数据维度和输出数据维度不同
# use_cudnn_on_gpu:一个可选布尔值,默认情况下是 True
# name:(可选)为这个操作取一个名字
# 输出:一个 Tensor,数据类型是 input 相同
使用示例如下:
input_data = tf.Variable( np.random.rand(10,9,9,3),
dtype = np.float32 )
filter_data = tf.Variable( np.random.rand(2, 2, 3, 2),
dtype = np.float32)
y = tf.nn.conv2d(input_data,
filter_data, strides = [1, 1, 1, 1], padding = 'SAME')
打印出 tf.shape(y)的结果是[10 9 9 2]。
(3)tf.nn.depthwise_conv2d (input, filter, strides, padding, rate=None, name=None,data_format= None)
这个函数输入张量的数据维度是[batch, in_height, in_width, in_channels],卷积核的维度是 [filter_height, filter_width, in_channels, channel_multiplier],在通道 in_channels 上面的卷积深度是1,depthwise_conv2d 函数将不同的卷积核独立地应用在 in_channels 的每个通道上(从通道 1 到通道 channel_multiplier),然后把所以的结果进行汇总。最后输出通道的总数是 in_channels * channel_multiplier。
使用示例如下:
input_data = tf.Variable( np.random.rand(10, 9, 9, 3),
dtype = np.float32 )
filter_data = tf.Variable( np.random.rand(2, 2, 3, 5),
dtype = np.float32)
y = tf.nn.depthwise_conv2d(input_data, filter_data,
strides = [1, 1, 1, 1], padding = 'SAME')
这里打印出 tf.shape(y)的结果是[10 9 9 15]。



pooling池化的作用则体现在降采样:保留显著特征、降低特征维度,增大kernel的感受野。另外一点值得注意:pooling也可以提供一些旋转不变性。
池化层可对提取到的特征信息进行降维,一方面使特征图变小,简化网络计算复杂度并在一定程度上避免过拟合的出现;一方面进行特征压缩,提取主要特征。


TensorFlow 中常见的分类函数主要有 sigmoid_cross_entropy_with_logits、softmax、log_softmax、softmax_cross_entropy_with_logits 等,它们也主要定义在 tensorflow-1.1.0/tensorflow/python/ops 的
nn.py 和 nn_ops.py 文件中。

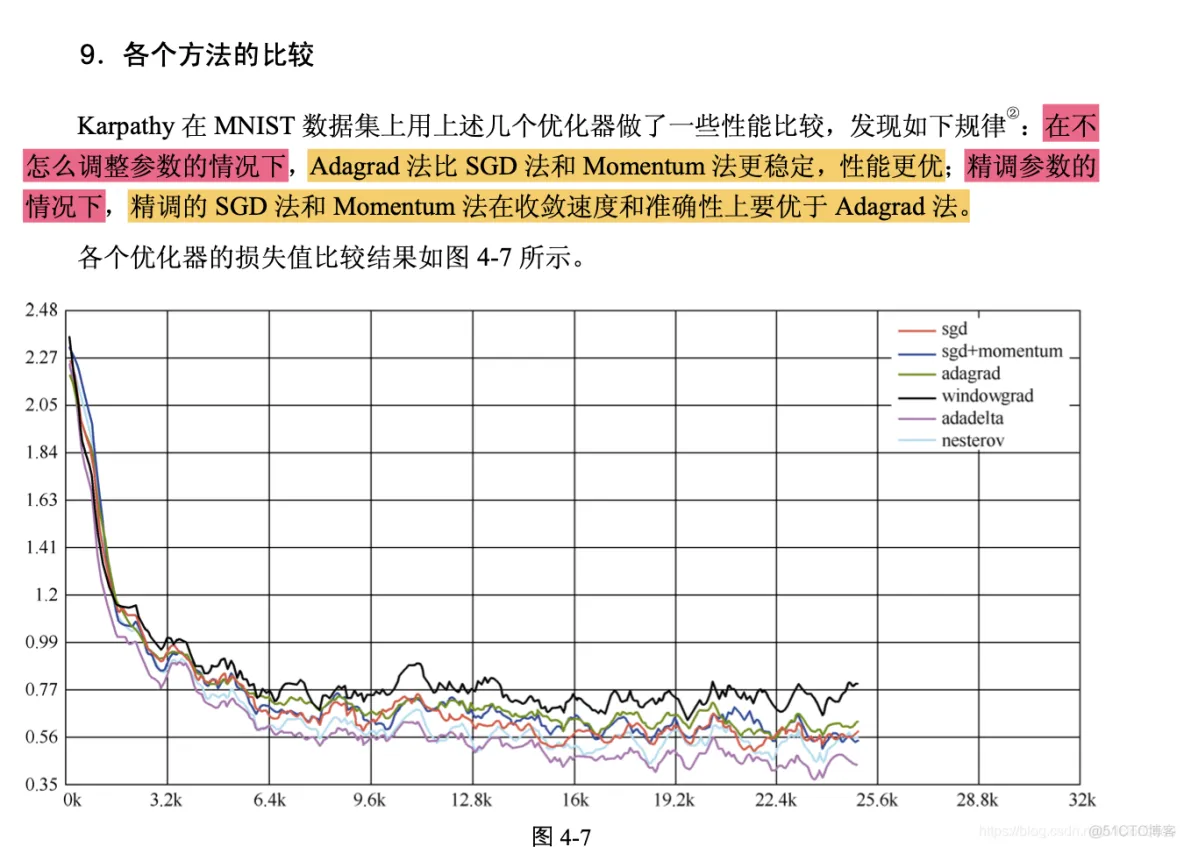
如何加速神经网络的训练呢?目前加速训练的优化方法基本都是基于梯度下降的,只是细 节上有些差异。梯度下降是求函数极值的一种方法,学习到最后就是求损失函数的极值问题。

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删