Delaunay细化网格生成技术揭秘

关键要点

• Delaunay 细化网格生成是平滑初始粗网格以捕获复杂几何结构中流固相互作用细节的过程。
• 该过程涉及将节点添加到现有网格并将流体和结构网格组合起来以精确捕获变形。
• CFD 工具提供专门的模拟选项，例如任意拉格朗日-欧拉，以解释流固耦合的影响。

计算流体动力学 (CFD) 中流动模型仿真的准确性在很大程度上取决于网格生成的质量。考虑到它们对各种几何形状的准确性和网格划分灵活性，用于生成三角形网格的选项是有效的。Delaunay 三角剖分是为高度定义的不规则几何体生成非重叠三角形的有用方法。

通常，必须实施一组特定的算法才能从 Delaunay 三角剖分中生成高质量的元素。这就是 Delaunay 细化网格生成的过程。让我们详细讨论这个概念，并探索它在捕获流体流动的流体-结构相互作用方面的好处。

Delaunay 细化网格生成

Delaunay 细化的主要目的是提高网格的质量。Delaunay 三角剖分包括将离散点集划分为一组符合 Delaunay 准则的非重叠三角形。需要注意两点：

• → 任何顶点都不应位于网格三角形的外接圆内。
• → 三角形最好是等角的，尽管可以使用不同大小的三角形。

因此，由于单元形状良好，生成的网格更加稳定，最大限度地减少了重叠引起的数值误差。

然而，这个初始网格很粗糙，需要细化以使其平滑。Delaunay 细化网格生成过程将额外的点插入到现有网格中，并使用 Delaunay 三角测量将它们连接起来以生成更精细的网格。这样的网格是详细的，因此计算是完成此任务的最可靠和最有效的方法。

这样的细化过程有几个优点：

1. 三角形轮廓分明，纵横比也很好。这最大限度地减少了模拟期间的计算错误。
2. 网格是分级的，即，它通过捕获具有适当网格分辨率的小尺度特征来改进复杂几何形状和流动模式的模拟。在曲率或大应力梯度区域周围，单元密度较高。
3. 当自动化时，细化过程减少了生成和优化网格所需的时间和精力，最大限度地减少了错误，并提高了网格的质量。

下图提供了 Delaunay 细化网格生成过程的基本概述。

使用 Delaunay 细化网格生成捕获流固耦合

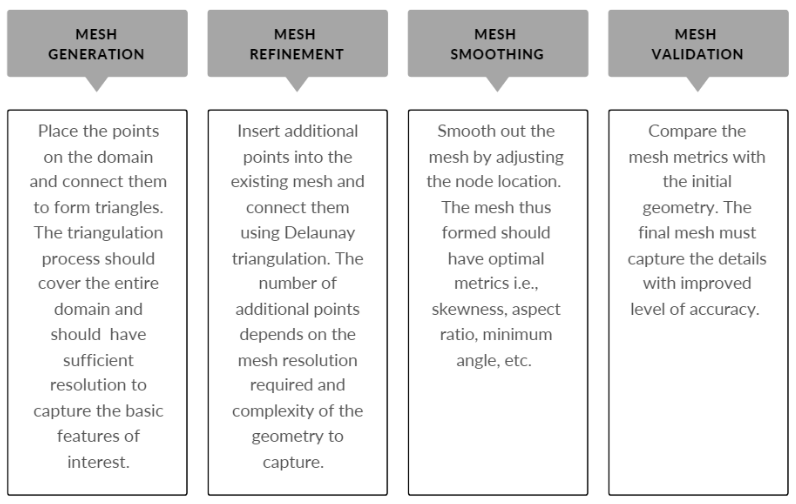
对于复杂的几何形状，Delaunay 细化网格生成有助于在 CFD 模拟中捕获流固耦合 (FSI)。FSI 分析在流体动力学中很重要，可以理解复杂的流体流动及其对固体结构变形的影响。可以使用以下方法在网格中生成和细化流体域和固体域的相互作用：

1. 离散化域。使用 Delaunay 三角剖分为整个流域生成粗网格。
2. 执行网格细化。在 Delaunay 细化网格生成之后，向网格添加额外的节点以优化分辨率并提高流体网格的质量。
3. 为实体结构生成网格。这可以使用专门的方法来完成，例如自适应 ALE* 网格划分或其他可以捕获实体结构变形的方法。
4. 结合流体和固体结构网格。定义适当的界面和边界条件以组合两个域。
5. 执行模拟。使用适当的 FSI 算法（例如 ALE*、CEL* 或 IBM*）。

*ALE - 任意拉格朗日-欧拉*CEL - 耦合欧拉-拉格朗日*IBM - 浸没边界法

使用 Delaunay 细化网格生成优化 CFD 中的 FSI 模拟

Delaunay 细化是捕获流体-表面相互作用的复杂细节的有效方法。CFD 工具可以生成带有 Delaunay 三角剖分的初始粗网格，可以通过向网格添加节点和元素来围绕实体结构对其进行细化，以实现最佳网格分辨率。CFD 工具通常提供专门的模拟选项，例如 ALE，它允许网格移动和变形以解决由于流体力引起的实体结构变形。

这种变形可以在 CFD 工具中可视化，以了解流动行为。网格运动的程度可以通过求解与网格相关的偏微分方程来计算。系统设计人员更喜欢使用 Cadence 的 CFD 求解器来计算这些用于网格细化的控制方程。通过生成高质量的网格，Fidelity Pointwise等 CFD 工具支持在广泛的航空航天、汽车或生物医学系统设计应用程序中对流固耦合进行可靠的模拟。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删