非结构化网格技术探秘：Voronoi图与Delaunay三角剖分

关键要点

• Voronoi 图和 Delaunay 三角剖分是生成非结构化网格复杂几何模拟的理想方法。
• Voronoi 图是 Delaunay 三角剖分的对偶。两者都使用相同的点集，并且适用于一个点的属性也适用于另一个点。
• 通过使用高阶网格划分流域，Voronoi 图和 Delaunay 三角剖分有助于深入了解流动行为。

在流体系统的计算分析中，用于模拟的网格生成是一种常用的方法。生成的网格可用于模拟广泛应用中的流动行为或传热行为，包括航空航天和汽车行业。

对于复杂的几何形状，可以使用 Voronoi 图和 Delaunay 三角剖分方法完成网格生成。在计算流体动力学 (CFD) 中，这些方法在网格划分过程中产生准确性和稳定性。让我们详细了解 Voronoi 图和Delaunay 三角剖分的概念，并分析它们对生成高质量网格的影响。

用于网格生成的 Voronoi 图和 Delaunay 三角剖分

在 CFD 分析中，系统设计人员寻求在几何域中表示真实的流动问题。网格生成将该域划分为有限数量的较小单元格，其中控制方程使用不同的技术离散化并求解以用于复杂工程问题的数值分析。这些网格可以是结构化的或非结构化的，具体取决于几何体的复杂性；但是，它们的质量是模拟准确性的极其重要的决定因素。

非结构化网格更灵活地表示复杂的几何形状，通常使用三角剖分方法来精确地表示此类复杂的域。Voronoi 图和 Delaunay 三角剖分通常用于生成非结构化网格。

德劳内三角剖分

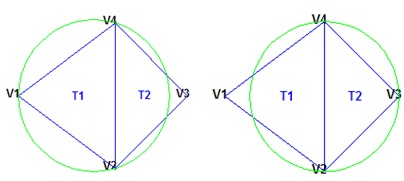
德劳内三角剖分

Delaunay 三角剖分是一种有助于将平面中的离散点集划分以形成一组三角形的算法。虽然有许多方法可以实现三角剖分，但 Delaunay 三角剖分的不同之处在于：

• 每个三角形的外接圆仅包含给定三角形的三个顶点。
• 这个三角形的外接圆内不存在顶点。
• 三角形是等角的或有非常轻微的变化。

如果生成的网格不够精细，可以通过插入额外的点来细化以提高分辨率。这种方法的优点是提高了精度并完全反映了几何的自然边界。

Delaunay 三角剖分的另一个好处包括构建 Voronoi 图。

维诺图

Voronoi 图是网格生成的过程，其中根据称为“站点”或“种子”的点的接近程度将平面划分为较小的区域。例如，假设有多个点散布在一个平面上。对于这些点中的每一个，绘制一条距离更近且与两个相邻点等距的线。Voronoi 图是通过这些线的连接形成的，它将域划分为一组多边形。

Voronoi 图也被认为是 Delaunay 三角剖分的对偶。鉴于这两种方法使用相同的点集，Delaunay 三角剖分的属性适用于 Voronoi 图，反之亦然。

Voronoi 图的含义 - Delaunay 三角剖分在 CFD 网格划分中

Delaunay 三角剖分算法和 Voronoi 图在 CFD 网格生成过程中具有许多优势，包括：

• 大量点的高效计算
• 适应复杂几何形状的灵活性
• 具有明确定义的单元的高质量网格划分
• 用于解决边界附近复杂性的自适应网格生成

可以使用以下 CFD 网格划分步骤来利用这些优势：

1. 定义流动几何并确定域的形状。
2. 生成一组有限的点以充分捕捉域内的几何复杂性。这些点将在 Voronoi 图和 Delaunay 三角剖分中引用。
3. 使用生成的点计算 Voronoi 图和 Delaunay 三角剖分以创建一组多边形和三角形。这可以使用 Bowyer-Watson 算法等技术来完成。
4. 定义边界条件以理想地表示边界处速度和温度等流动参数的影响。
5. 如果需要改进网格以提高网格的分辨率和精度。
6. 使用 CFD 求解器运行仿真并通过求解控制方程来分析流体流动行为。

高质量网格生成以提高仿真精度

网格质量越高，对流体系统行为的分析就越准确。Voronoi 图和 Delaunay 三角剖分等工具有助于生成非结构化网格以定义复杂的几何流域。在此域中，可以离散化和求解控制偏微分方程，以了解流动行为及其对结构的影响。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删