抽象的：非结构化网格划分方法因其不断提高的自动化程度而获得关注，周转速度比结构化网格技术快得多，但在质量和流动解决方案精度方面，流动域内部的四面体仍然无法替代结构化单元。与其选择结构化网格形式，不如用 Cadence® Fidelity™ Pointwise™ Mesh Generation 的六核体素网格替换大量非结构化四面体，可以保留结构化网格提供的截断误差消除。体素网格化从少量根体素元素开始，然后通过八叉树框架将其细化为尺寸字段规范。体素元素被分类为切割、在规定的表面网格内部或外部，从而导致元素集完全在表面网格边界之外。

为什么要改进非结构化 Tet 网格？

三十年前，结构化（映射）网格是 CFD 研究和应用中的主要网格类型。随着几何形状复杂性的增加，多块结构化网格的构建很快成为解决方案周转的瓶颈。这些限制启动了对更有效的网格方法（即非结构化四面体网格）的研究，以自动填充一般空隙。

尽管这些方法的应用自动化程度不断提高，周转速度比结构化网格技术快得多，但在质量和流动解决方案精度方面，在流域内部使用四面体仍然不能很好地替代结构化单元。此外，tet 网格的生成成本很高，而且它们的求解精度可能会降低。

二进制和八叉树结构

典型的空间二叉树数据结构是节点的层次网络，每个节点包含三个指针（父节点、左节点和右节点），节点角的六个实数，每个节点中根以下的层数分裂方向，以及节点子节点的分裂方向。典型的空间八叉树数据结构类似，每个节点包含九个指针（父节点和八个子节点）、节点角的六个实数以及根以下的层数。

虽然二叉树的节点包含较少的数据，但需要更多的节点来表示与八叉树相同的分区。通过使用存储指向子节点的固定长度数组的单个指针的块表示，可以进一步减小数据结构的大小。这通过从节点中删除七个指针来增加八叉树节点的好处，而它仅通过单个指针减少二叉树节点。

八叉树数据结构的另一个优点是易于对数据结构内的节点位置进行编码。当数据结构从根节点遍历到给定节点时，此位置代码是八叉树每个级别的子索引。

各向同性六角核心网格

一种避免四面体网格中几何随机性的技术是用一组笛卡尔对齐的六角立方体或体素替换各向同性四面体。这样，棱镜和六边形单元仍然可以用来解决近体现象，而体素单元可以用来更好地解决一些离体区域包含梯度的问题。由于大小字段会在空间上发生变化，因此通过将体素重复细分为由八叉树框架控制的八分圆来允许体素细化是合乎逻辑的。

八叉树方法允许相邻体素上的面不相交，因为没有定义明确的连接。正如将要讨论的那样，通过将体素转换为占据与体素相同空间的六角核心网格来强制执行严格的细胞到细胞连接。

根体素

各向同性体素网格化已以三种相似但不同的模式实施到 Fidelity Pointwise 中。这些方法中的每一种都从构建根体素系统开始，其中根体素尺寸很小，同时仍然允许体素大小在 x、y 和 z 方向上保持一致。根体素的初始尺寸是根据用户设置的范围框纵横比计算的。

1. 在外部模式下，块范围是用户指定的，任意数量的用户选择的封闭和开放表面网格被插入到块中，从而产生一个共形网格，其中包含外部和表面的体素和/或内部的各向异性网格块内部。

图 1. 外部模式体素网格

1. 在内部模式中，规定了一个封闭的外部边界和零个或多个封闭和开放的内部边界，并且在外部边界内部和可能的内部边界外部形成体素。虽然这种类型的网格通常表示内部流动几何形状，但它们也可以用于外部边界需要遵守规定的网格或间距的情况，例如当两个或多个块彼此相邻时。

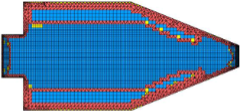
图 2. 内部模式体素网格

体素细化

一旦根维度和范围框被计算出来，根体素就会被递归地细化以匹配局部尺寸字段。在下面的大纲中，目标级别等于满足大小字段所需的根体素的二元划分数。

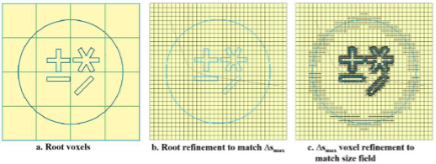
图 3. 根体素的初始细化

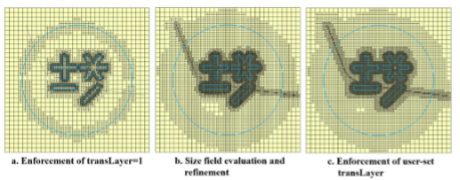
图 4. 跨层执行和进一步的体素细化

体素分类

此时的网格将由完全包围表面和边界网格的矩形体素块组成，每个体素都细化到大小字段指定的级别。在本节中，体素将被分类为切割边界网格 (cut)、位于边界网格外 (out) 或位于边界内 (in)——后一种分类代表唯一的非丢弃集。

1. 如果体素或三角形的任何部分通过相交或相邻占据相同的空间，则体素单元切割三角形。每个三角形最终必须针对每个体素（笛卡尔形状）进行交叉测试。
2. 进/出体素：在上一节中未被识别为剪切的体素现在将被分类为进或出。只有少量体素，特别是每个相邻体素区域一个，需要明确分类。所有其他体素将通过分类体素的递归泛洪填充分配进/出状态。

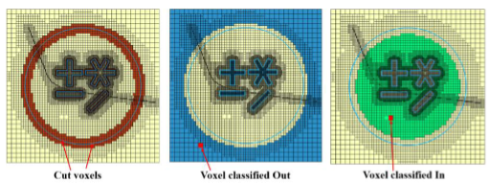
图 5. cut、out 和 in voxels 的分类

属于不同组号的体素将对应于体素的物理上不相交的区域。分类完成后，对分配给每个区域的体素数进行统计，并且标记出属于包含少于体素总数 1% 的组的体素。这可以防止网格中出现非常小的体素袋（与四元组隔离没有优势）。

体素转换为六角核心形式

通过用单个六角形或一小组占据相同物理空间的四面体和金字塔替换每个体素矩形，将体素表示转换为六角形核心形式（棱镜不是从体素创建的）。

首先枚举代表标记为 In 的所有体素角的 xyz 顶点列表。接下来，检查每个体素与其相邻体素的面部一致性。如果所有六个面都完全匹配相邻的单元面（或表示边界），则体素将导出为十六进制元素。对于所有其他情况，将至少有一个体素面孔，其邻居的面孔是该面孔的子集或超集。当邻居细化附加层时，将这些单元格转换为一般元素可以简单地通过用四个面替换体素中的一个面来进行。然而，转换为四角形、金字塔形和六角形需要更复杂的逻辑。通常，只有不同细化级别的体素之间的层中的单元区域需要转换为四面体和金字塔。

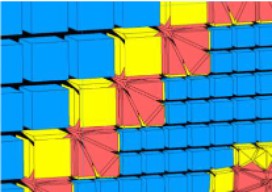
图 6. 过渡金字塔和连接十六进制细化级别的四边形

前沿分类和各向同性 Tet 生成

剩余的要用网格元素填充的空隙是“拉链”区域——那些由表面网格和六角形核心单元的边界界定的区域。然而，可能存在多个封闭和开放的表面网格和六角形核心边界，这极大地复杂化了代表各个网格区域的单元格的正确分组。

幸运的是，可以实施一些简单的启发式方法来识别应该匹配哪些表面。首先，表面网格和六核边界网格被独立地划分为流形前沿，定向使得方向上的法线点尚未被填充。对于六核网格，所有前沿都是封闭的，但如果在网格中插入了挡板，则表面网格上可能存在开放前沿。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删