粘度是影响流体行为和边界层形成的关键流体特性。粘度导致流动流体的速度在与固体表面接触并受到摩擦力时减慢。速度从自由流下降到表面附近的零,形成薄层,称为边界层。
但是当流体没有任何粘性时会发生什么?在无粘流中,没有粘性意味着形成的边界层很薄,可以认为不存在,即表面附近和表面以外的压力相同。但是固体表面仍然影响流动。在本文中,我们将研究无粘流中的边界层方程,以探索边界条件如何影响流体行为以及 CFD 如何帮助分析这种行为。
无粘流是指粘性力可以忽略不计的流体流动类型,即流体与接触表面之间的摩擦力为零。因此,在这种流动中没有剪应力,在分析过程中只能考虑法向应力。此类流动模型可用于流体应用中流动行为的理论分析,包括空气动力学设计、天气模式预测或流体动力学分析。
由于缺乏粘性,无粘性流动的边界层方程不适用。在这种情况下,只要适当指定边界条件,就可以使用欧拉方程分析流场。欧拉方程基于无粘性流动的无滑移边界条件,这表明边界处的流体速度为零。
一般的边界层方程可以用Navier-Stokes 方程表示:
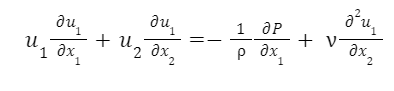
此处,ν 是运动粘度,ρ 是流体密度,P 是流体的压力。u 1和u 2分别 是沿方向x 1和x 2的速度。
对于无粘流,上式可以简化为:
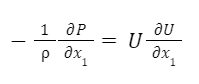
U 是流体的速度。
上述欧拉方程有助于理解非粘性流动时边界附近的速度和压力分布。靠近表面的速度很低,并在上游不断增加,直到达到自由流速度。对该流速和相关雷诺数的研究有助于预测流动模式和湍流的发生,这有利于空气动力学和流体动力学设计。
CFD 一直是系统设计人员用来预测复杂系统设计的流动行为的流行工具。虽然无粘流对于实际应用可能不实用,但简化的流动模型可以帮助对流体行为进行初步估计,从而确定优化区域。以下是 CFD 如何帮助分析无粘流中的边界层方程:
| 数值分析 | CFD 工具可用于求解与边界层相关的偏微分方程。数值分析有助于理解流动行为和流动可能分离或变成湍流的过渡区域。 |
| 流动分离 | 在无粘流中,当方向突然改变时,流动可能会分离。压力的突然降低和速度的增加可能导致流体从表面分离。可以通过速度场和压力场的 CFD 模拟来评估流动分离。 |
| 边界层厚度 | CFD通过确定从表面到流体达到 99% 自由流速度的位置的距离来预测边界层的厚度。为此,必须指定边界条件,包括无粘流的无滑移条件。 |
| 系统优化 | 表面周围流动行为的模拟有助于分析不同的设计概念。然后可以比较不同的结果以优化设计以获得最大效率。 |
无粘流中边界层参数的数值分析可以通过求解与流动相关的偏微分方程组来完成。CFD 求解器可以通过使用欧拉方程对无粘流进行建模和分析来帮助进行此分析。从仿真中获得的结果是确定流体系统中速度和压力分布的关键,这对于理解流动的关键变化非常重要;例如,分离、湍流、冲击波和涡流。利用CFD进行数值模拟和分析,工程师可以轻松求解无粘流中的边界层方程,便于对复杂流体系统进行评估和优化。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删