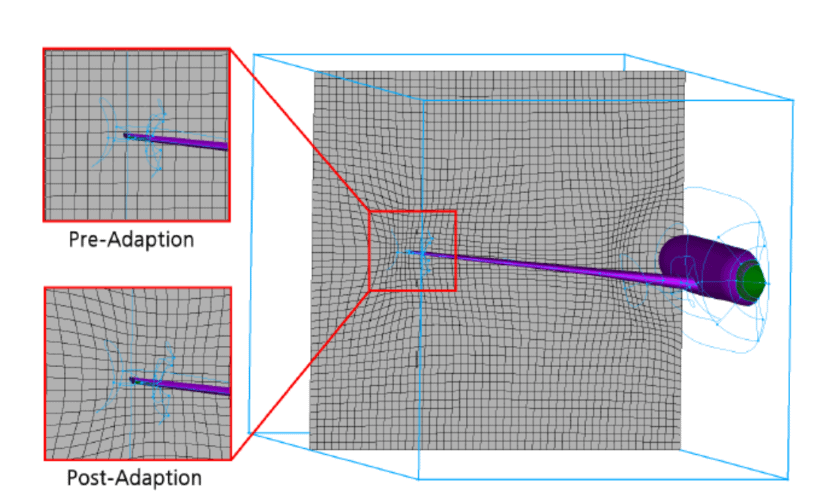
计算流体动力学 (CFD)模拟的基础是生成高质量的网格。网格划分过程将感兴趣的域离散化为有限数量的小几何元素,在这些元素中求解应用的控制方程以进行流体运动分析。在许多情况下,准确捕获几何图形及其特征可能是一项挑战。通过网格变形,可以对网格进行修改以提高 CFD 模拟的准确性。
CFD 中使用不同的网格变形技术对网格进行修改,以便更好地表示问题的几何形状并确保效率模拟。本文将概述网格变形过程及其各种技术。
网格变形是在不影响流体流动域的基础几何结构的情况下对网格进行修改的过程。在 CFD 中,当初始域不能代表手头的问题时,可能需要进行修改。例如,当流体力导致结构变形时,可能需要网格变形来分析这种变化。同样,在优化研究中,可能需要网格变形来探索不同的设计变化。
对于网格变形,移动网格中的节点和顶点。这是以受控方式完成的,因此不会损害网格的连接性。这种网格变形过程在 CFD 分析中具有以下优势:
网格变形的上述重要性可用于 CFD 中,使用不同类型的网格变形技术,我们将进一步讨论。
网格变形方法可以分为两类——传统的基于网格的方法和无网格方法。
基于网格的变形技术考虑了固定网格的作用,并依赖于网格的顶点或节点的受控移动来解释变形或其他几何变化。基于网格的方法可以进一步分为以下技术:
| 基于变形 | 网格通过节点和顶点的受控移动而变形。例如,自由变形技术。 |
| 基于网格 | 网格被离散化为单元网格以表示流体域。每个单元独立变形以详细捕捉流固相互作用。例如,格子玻尔兹曼方法。 |
| 基于水平集 | 使用水平集函数,其中为网格中的每个点分配一个值,表示到流体界面的距离。然后通过移动点来模拟流固耦合来完成网格变形。例如浸入边界法。 |
| 基于优化 | 网格变形基于衡量网格质量的成本函数。将节点的坐标调整到最佳点以提高仿真精度。 |
无网格方法不依赖于固定的网格结构。相反,它使用一组节点表示域。可以通过以受控方式重新定位这些节点来解决变形问题。无网格方法可能包括以下方法:
| 径向基函数 (RBF) 插值 | 离散控制点集和径向基函数用于插值。 这是通过评估 RBF 并根据相关控制点的位移值对它们进行加权来完成的。 |
| 移动最小二乘 (MLS) 插值 | 多项式函数用于对每个节点处的位移值进行插值。 多项式函数最小化数据点和多项式函数之间的最小二乘误差。 |
| 平滑粒子流体动力学 (SPH) | 流体由一组离散的移动粒子表示,并且进行内核近似以在任何给定点插入粒子属性。 |
| 无元素伽辽金 (EFG) | 该域由一组节点离散化,并且使用基函数的加权组合来计算任何特定节点处的解。 |
网格变形是一种解决方案,可以准确地对流域中的问题进行修改,而不会产生失真等问题。由于其灵活性和效率,工程师和系统设计师广泛执行网格变形以提高 CFD 仿真的质量。CFD 工具可以根据需要使用基于网格或无网格的网格变形方法。通常,基于网格的方法用于定义明确的几何体,而无网格方法用于边界不断变化的复杂问题。
使用 Cadence 的 CFD 求解器等工具,可以高效地执行网格离散化、变形、插值和修改,以解决流动和边界条件的变化。通过更好地表示流动问题,可以准确预测流动行为和变形,以实现高效模拟和设计优化。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删