计算流体动力学 (CFD)本质上是一系列近似值,CFD 从业者的职责是管理这些近似值中的误差大小。最基本的近似值之一在于用于模拟的细胞类型。近似值可以是好的(地球是球形的)也可以是坏的(地球是平的)。两者都可以根据用户的观点和目标服务于一个目的。CFD 从业者必须决定几个模拟方面,例如求解算法、湍流模型和收敛方案。同时,了解他们对计算网格的选择的后果对于生成高保真模拟结果至关重要。

在 CFD 进入画面之前,需要选择离散化方案。关于计算网格的决策需要对求解器有很好的了解——它支持什么类型的单元格?它对与网格相关的错误有多敏感?– 及其对计算网格的控制。理想情况下,网格将仅由流动对齐的正交六面体单元组成,但这种方法不适用于复杂的几何形状。此外,在高梯度区域中未充分细化的网格可能会通过低估流动中存在的剪切而对解决方案产生不利影响。按照这些思路,在 CFD 工作流程中做出的选择将最终决定解决方案的适用性和可信度。
由于 Navier-Stokes 方程解中固有的动力学复杂性,评估任意情况下由网格引入的误差具有挑战性。在检查网格的影响时,Navier-Stokes 方程中的对流导数似乎是一个合适的候选者(由于其非线性性质)。
在本研究中,考虑了被动标量平流情况,并采用了仅平流求解器。这项工作展示了给定求解器的网格类型之间的基线差异,理解更复杂的算法可能会提高解决方案的质量,但趋势将保持不变。
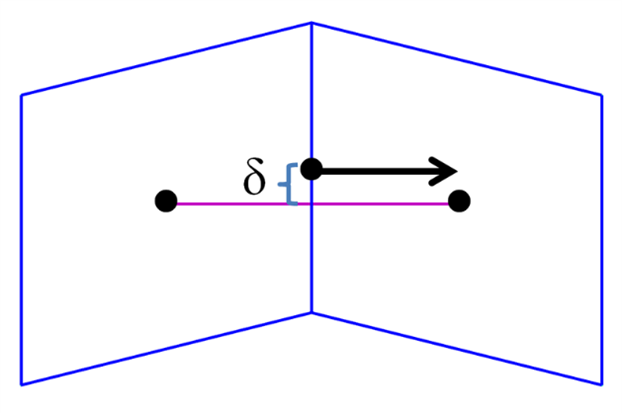
图 1. 在存在垂直梯度的情况下,面中心与连接单元中心的线(单元偏度)之间的偏移量 δ 会影响共享面的计算通量的准确性,从而引入数值误差。
这种类型的错误主要影响平流项,例如 Navier-Stokes 方程中的对流导数。该术语驱动了湍流中存在的许多非线性,任何错误陈述都会对模拟精度产生不利影响,特别是对于具有离体梯度的分离流。
图 2 说明了一个简单的 2D 案例,其中热剖面在模拟域中平流。
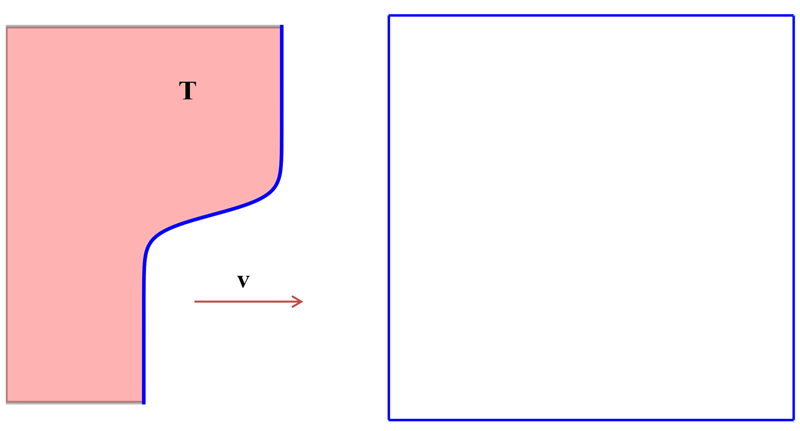
图 2. 该图显示了由矩形域组成的测试用例和施加的热梯度,该梯度将平流穿过模拟体积。
这里的误差是从纯四边形网格考虑的。解决方案中存在的小误差只是有限离散化大小导致的基线插值误差。也就是说,解决方案中存在的错误完全是由于网格分辨率的限制,而不是电池质量差的结果。
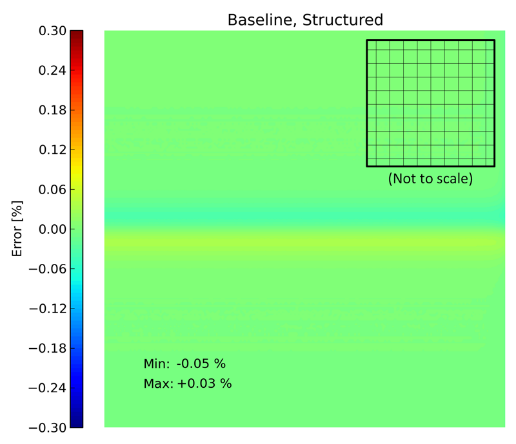
图 3. 在具有四边形元素的正交网格上计算的解决方案中的基线误差显示完全由分辨率限制引起的误差。
然后可以将这些结果与两个具有三角形元素的非结构化网格的计算结果进行比较。第一个是使用 Delaunay 算法生成的,具有非零偏度的单元分布,如图 4 所示,可以清楚地看到偏度对解决方案准确性的影响。使用 Advancing Front 算法生成的第二个非结构化网格包含在大部分计算域中具有零偏度的等边三角形。
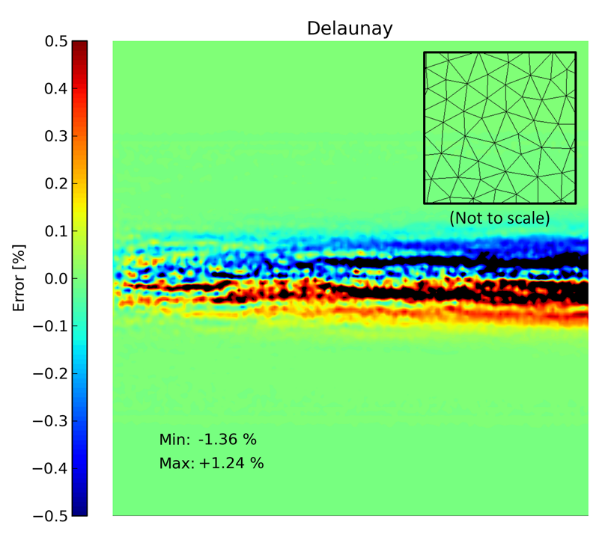
图 4. 在 Delaunay 三角网格上计算的解的误差比结构化网格的误差高得多。
非零偏度可能是对任何有用的几何体建模不可避免的结果。然而,这项研究旨在激励希望尽量减少与网格相关的错误的研究人员。对预期流场的直观预见指导经验丰富的 CFD 从业者隔离感兴趣的关键区域并最大限度地提高该区域的细胞质量。
这些简单的二维示例可以扩展到三维,如图 6 所示。与图 3 所示的结构化案例一样,产生的误差完全是由于分辨率的限制。

图 6. 具有强加高斯温度分布的立方域将简单问题扩展到三维。
这些结果并未说明要避免非结构化网格。相反,这些结果来自专门设计用于突出网格对解决方案的影响的隔离测试用例。
现代 CFD 求解器可以在六面体和四面体网格上生成稳健的解(当然取决于求解器)。此外,用于计算这些结果的简单算法缺乏许多现有技术来减轻求解器中可能存在的不良细胞质量的影响。最后,所讨论的错误通常会随着网格分辨率的增加而减少。因此,如果网格足够精细,这些错误是无关紧要的。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删