很多同学在采用实体单元进行模拟时,需要施加扭矩,然而实体单元节点只有平动自由度,因而不能类似梁单元那般直接施加扭矩,今日水哥就ANSYS中常见的实体单元施加扭矩方法做一个简单的总结,希望对部分同学能有所裨益!
实体单元施加扭矩的方法常见思路有两种:
一、扭矩实质是矩,是力和力臂的乘积,因而如果要施加扭矩,可以考虑将扭矩折算为力和力臂,直接在相应部分施加力即可。
二、实体单元之所以不能直接在节点上施加力矩,说白了就是节点无转动自由度,因而只要我们引入了具有转动自由度的节点,在进行一定的耦合操作,就可以实现扭矩的输入。
第一种思路很简单,水哥这里就不详细阐明。这里重点说说第二种思路。
引入转动自由度在进行一定的耦合,常见的方法有两种,一种是cerig刚性区域法,另外一种是mpc184刚性梁法。其实还有一种方法,rbe3,但这种方法较为复杂,这儿不做推荐。
一、cerig刚性区域法
cerig 这个命令其实就是建立一定的刚性区域,然后将荷载施加在跟这个刚性区域相连的主节点(master node)上。而具有转动自由度的节点,我们经常引入质量单元mass21,赋值时候对质量单元赋予很小的质量即可。
该方法本质上是建立了约束方程,但需要特别注意的是约束方程是线性的,因而该方法只使用于线性问题,对于大变形等非线性问题,该方法并不适用。
二、MPC184刚性梁法
刚性梁相信大家并不陌生,其主要引入的单元便是ANSYS中最为特殊的单元MPC184,通过设置单元实常数,使其该单元成为刚性梁,在具体使用过程中,需要在构件中心部分建立一个节点,跟其他受力节点分别形成多根刚性梁,从而形成刚性面,最后直接在构件中心节点施加荷载,通过刚性梁来传递荷载。
该方法适用范围相对刚性区域法来讲更广,对于大应变分析也能很好的使用。
下面以一个简单的例子来简单演示两种方法的具体使用过程。
题目:某长方体块,材料为钢材,截面尺寸为10mmX10mmX30mm,一端固定,另一端承受 1 N.m的扭矩,采用上述两种方法求解该模型。
一、cerig刚性区域法
finish
/clear
/prep7
et,1,solid186
et,2,mass21
r,2,1e-6
mp,ex,1,2.0e5
mp,prxy,1,0.3
mp,dens,1,7850e-12
blc4,,,10,10,30
esize,2
vmesh,all
!=========
*get,nodemax,node,0,num,maxd
n,nodemax+1,5,5,35
type,2
real,2
e,nodemax+1
!===============
!建立刚性区域
nsel,s,loc,z,30
nsel,a,,,nodemax+1
cerig,nodemax+1,all,all
!===================
f,nodemax+1,mz,1e3
nsel,s,loc,z,0
d,all,all,0
!==============
/solu
allsel,all
solve
二、MPC184刚性梁法
finish
/clear
/prep7
et,1,solid186
et,2,mpc184
keyopt,2,1,1
mp,ex,1,2.0e5
mp,prxy,1,0.3
mp,dens,1,7850e-12
blc4,,,10,10,30
esize,2
vmesh,all
!================
*get,nodemax,node,0,num,maxd
n,nodemax+1,5,5,35
nsel,s,loc,z,30
*get,node1,node,0,num,max
*get,node2,node,0,num,min
num1=node1-node2
type,2
e,nodemax+1,node2
*do,i,1,num1
e,nodemax+1,node2+i
*enddo
!=======
/solu
allsel,all
f,nodemax+1,mz,1e3
nsel,s,loc,z,0
d,all,all,0
allsel,all
solve
两者模型对比情况如下:
刚性区域模型
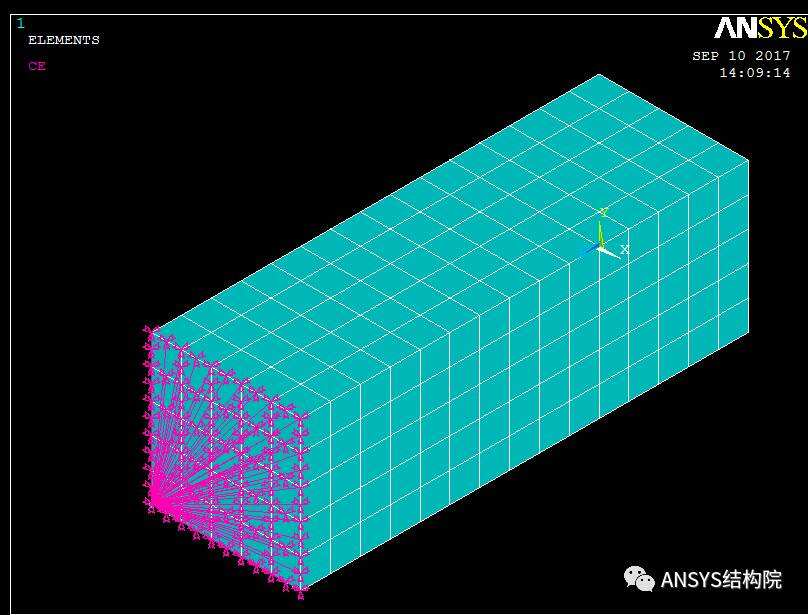
刚性梁模型

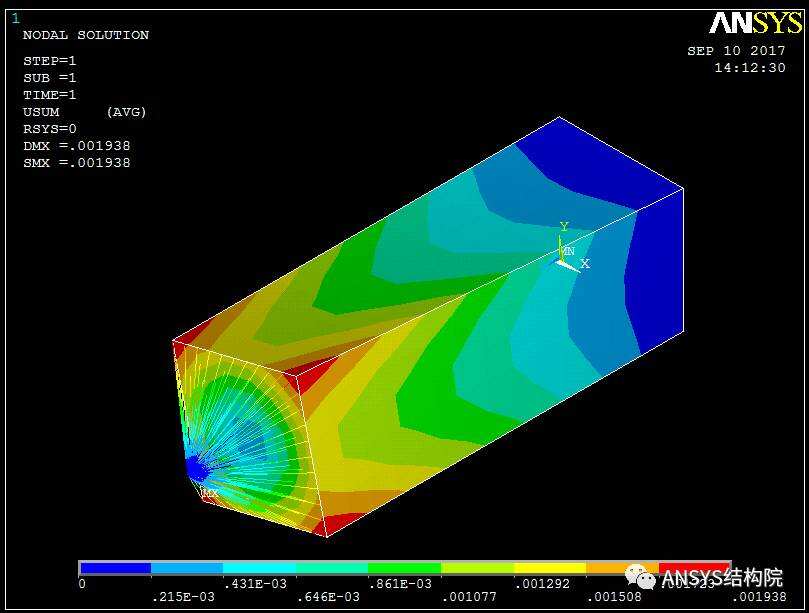
刚性区域位移云图
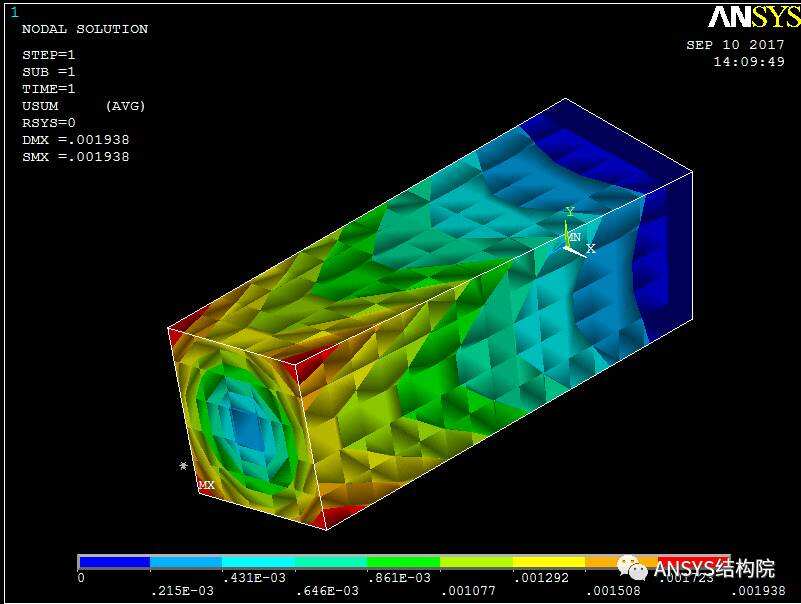
刚性梁位移云图
刚性区域von mise应力云图
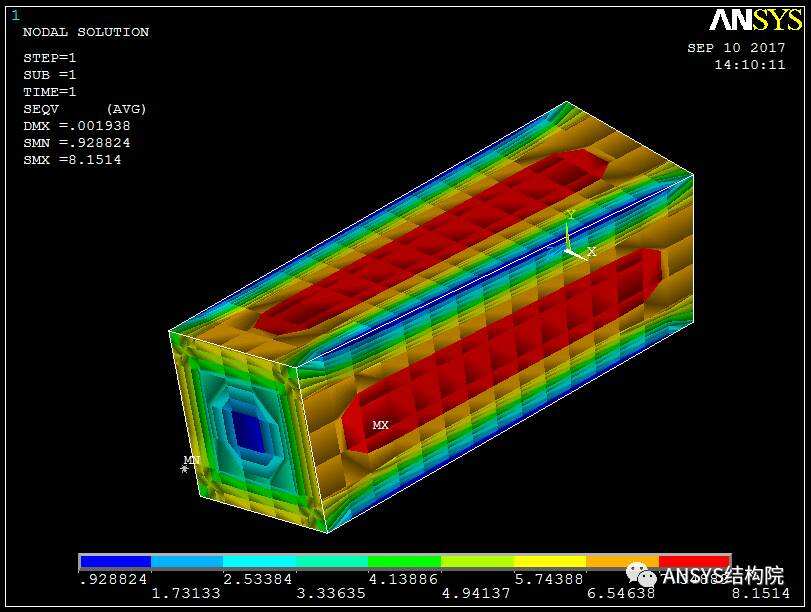
刚性梁von mise应力云图
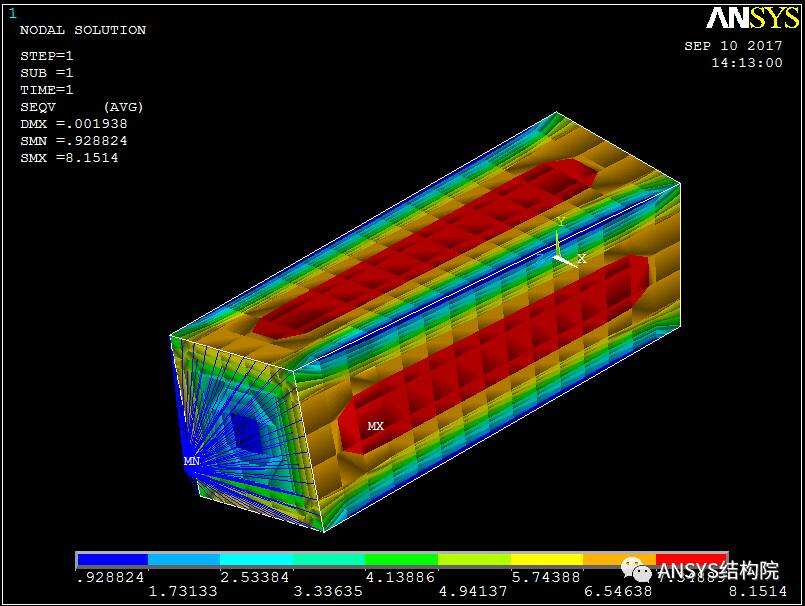
对比上图可见,两者结果一致。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删