一、实物模型演示
一个单独的钢尺和一个由两个相同的钢尺栓接在一起的组合钢尺,如图1(1)所示,以悬臂的形式并排在一起。对这两个钢尺的悬臂端施加相同的初位移,然后同时迅速释放,使之产生自由振动。可以发现,由两块组合的钢尺要比单块钢尺更快停止振动,见如图1(2)。

1) 施加相同的初始位移

2)两块组合的钢尺要比单块钢尺更快停止振动
图1 自由振动衰减与结构固有频率的关系
本模型演示表明,结构的固有频率越高,其自由振动衰减越快。
二、问题描述
假设钢板尺子的长度L= 0.5 m,宽度h = 40mm,厚度b = 2 mm。弹性模量E = 200 GPa,泊松比u= 0.3,密度 7800 kg/m3。分别计算单独的钢尺和组合钢尺的振动情况。

三、问题分析
一端用压在桌子上,可处理成固定端,约束可处理成全固定。悬臂端施加相同的初位移,然后松手释放,约束可处理成自由边界。

由此可见,振幅对数衰减率仅取决于阻尼比。本算例初始的振幅相同,振幅对数衰减率也一样,但是组合钢尺的固有频率是单块钢尺的2倍,组合钢尺振动快一些,其自由振动的衰减也就快一些。因此,从理论上证实前面的概念:结构的固有频率越高,其自由振动的衰减越快。
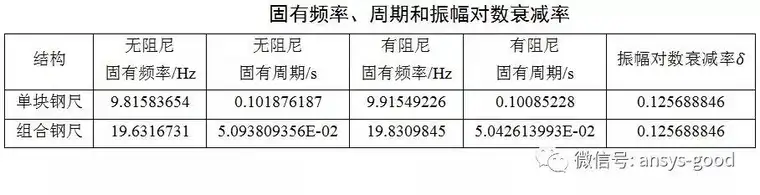
在ANSYS计算中,不是直接输入阻尼比。而是通过对数衰减率δ、阻尼系数c、α质量阻尼或者β刚度阻尼等方式输入的。本算例考虑阻尼,采用振幅对数衰减率输入。下表给出了两种结构的固有频率、周期和振幅对数衰减率。
ANSYS分析主要步骤:
1)建模,进行模态分析,求出固有频率。
2)在悬臂端施加集中力,进行静力学分析。得到各节点的初位移数值,初位移包括初始挠度和初始转角。
3)进行瞬态动力学分析,施加振幅对数衰减率。在第1载荷步,关闭时间积分影响,施加初位移;第2载荷步,时间积分时间增量取一个周期的1/60,保存每个子步的结果进行求解。在时间历程后处理中,得到的挠度随时间变化曲线见图3。
由此可见,组合钢尺的振动周期的时间短固有频率高,组合钢尺比单个钢尺衰减得更快一些。
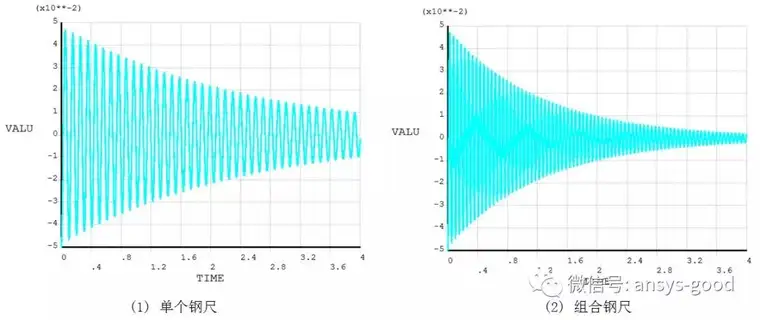
图3 挠度随时间变化
四、命令流
Ex1=2e11 !弹性模量Pa
b1=1*3e-3 !截面宽度m,修改此处b1=2*3e-3
h1=40e-3 !截面长度m
L1=0.5 !长度m
rou1=7800 !密度
m1=b1*h1*rou1 !单位长度的质量
I1=h1*b1**3/12 !惯性矩
pi=acos(-1)
k1=(Ex1*I1/(m1*L1**4))**0.5
Fre0=3.516/(2*pi)*k1 !第1阶固有频率解析解Hz
T0=1/Fre0 !第1阶固有周期s
kesi=0.02 !阻尼比或相对阻尼系数0.02
Fre1=Fre0/(1-kesi)**0.5 !有阻尼条件下第1阶固有频率
T1=1/Fre1 !有阻尼条件下第1阶固有周期s
!c1=2*kesi*m1*L1*(2*pi*Fre1) !阻尼系数,好像有问题
afa1=2*kesi*(2*pi*Fre1)
uy1=0.05 !假定的初位移
F1=3*Ex1*I1*uy1/L1**3 !悬臂梁已知初位移求载荷
/PREP7
ET,1,BEAM188 !单元类型
KEYOPT,1,3,3 !形函数
MP,EX,1,Ex1 !材料属性Pa
MP,PRXY,1,0.3
MP,DENS,1,rou1
!MP,DMPR,1,kesi !阻尼比
SECTYPE,1,BEAM,RECT,,0 !截面属性m
SECOFFSET,CENT
SECDATA,b1,h1
K,1,0,0,0 !关键点mm
K,2,L1,0,0
L,1,2 !线
/PNUM,KP,1 !关键点编号
/PNUM,LINE,1 !线编号
LATT,1,,1,,,,1 !线的单元属性
LESIZE,all,,,20 !单元份数
LMESH,ALL !线分网
/ESHAPE,1.0 !单元形状
DK,1,ALL !施加位移约束
FINISH
/SOLU
ANTYPE,2 !模态分析
MODOPT,LANB,6
MODOPT,LANB,6,0,0,,OFF
SOLVE
FINISH
/POST1
SET,LIST
fre=Fre1
/SOLU
ANTYPE,0 !静力求解
FK,2,FY,-F1 !集中力N
SOLVE !求解
FINISH
/POST1
*DIM,uyy,ARRAY,21,3,1 !数组
*do,i,1,21
uyy(i,1)=i !节点号
uyy(i,2)=uy(i) !挠度
uyy(i,3)=rotz(i) !转角
*enddo
FINISH
/SOLU
ANTYPE,4 !瞬态动力学
TRNOPT,FULL
TIMINT,ON
delta=2*pi*kesi/(1-kesi**2)**0.5 !对数衰减率
GAMMA=delta
TINTP,GAMMA
TIMINT,OFF !时间积分影响关闭
TIME,1e-6 !小的时间增量
NSUBST,2 !两个载荷步
KBC,1 !阶跃
FKDELE,2,FY !删除载荷
*do,i,1,21
D,uyy(i,1),UY,uyy(i,2) !施加初位移
D,uyy(i,1),ROTZ,uyy(i,3)
*enddo
SOLVE !求解
TIMINT,1 !打开时间积分影响
DELTIM,1/fre1/60,0,0 !时间增量,一个周期计算60次
OUTRES,ALL,1 !输出每步的结果
DDELE,ALL,all !删除初位移约束
D,1,all !施加固定端约束
KBC,0 !斜坡
TIME,20*1/fre1 !计算时间20个周期
TIME,4 !计算时间4s
!ALPHAD,afa1
SOLVE !求解
FINISH
/POST26 !时间历程后处理
FILE,'file','rst','.'
NSOL,2,2,U,Y,
XVAR,1
/YRANGE,-uy1,uy1,1
PLVAR,2, !挠度曲线
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删