ANSYS模态计算：原理与实战详解

如图1给出了结构振动计算中各模块之间的关系，由此可见模态计算是振动冲击计算的基础为其他模块提供了相应的数据支撑。

图1 结构振动计算中各模块之间的关系

模态分析用于确定机械部件的振动特性，即结构的固有频率、振型、振型参与系数和有效质量，它们是结构承受动态载荷设计中的重要参数。

结构整体的动力平衡方程：

其中：[M]-总体质量矩阵；[C]-总体阻尼矩阵；[K]-总体刚度矩阵；{u}-节点位移；{Fa}-结构的外部随时间变化的载荷。
 

模态计算中，假设条件之一：结构没有外载荷，即结构是自由振动；所以（1）式变为：

对于大多数问题，模态计算都是忽律阻尼的影响（这是为什么呢？请读者往下看），因此对于无阻尼模态计算，（2）式可以转换为

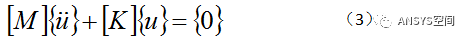
再利用模态的另一个假设条件：

结构是线性的，即具有恒定的总体质量矩阵和总体刚度矩阵，则可以得到方程（3）的变形通解为：
 

（4）把（4）式代入（3）式，消去时间变量，得

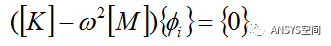
（5）上述方程的成立的两种情况：

（1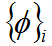）= 0：表明结构没有振动，这个情况不考虑舍去；

（2）

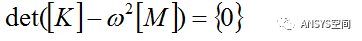
  求解上述方程，可以求解出n个方程的根

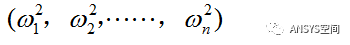
对于每一根（特征值），都对应着一个特征向量

对于单自由度弹簧振子系统，有以下结论：

无阻尼的结构固有频率：

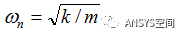
考虑阻尼的结构振动频率

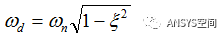
由上述两式可知，对于一般结构的阻尼比都小于0.1，因此有阻尼的固有频率和无阻尼的固有频率基本一致，因此大部分问题，在模态计算中是忽律阻尼的，但是对于振动系统中存在阻尼器的问题，就需要考虑阻尼对其固有频率的影响。

通过模态计算的理论推导可以得到以下结论：

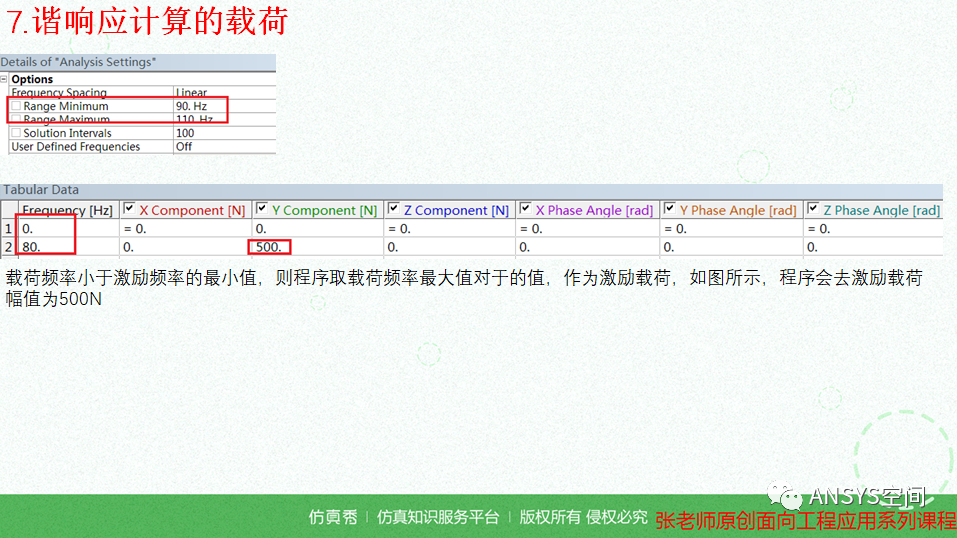
1）-模态计算是自由振动，因此模态计算中不支持力载荷，软件操作也证明了这一点：

2）-影响模态计算结果的两个主要因素：结构刚度和结构质量，其中结构质量主要和材料属性有关，但是结构刚度的影响因素就较多了。

3）结构刚度主要由：材料属性，结构特征和连接关系确定，材料属性即弹性模量，结构特征即产品的结构特点，连接关系即单体部件的约束方式和装配体部件中不同子部件的连接刚度。

4）对于复杂结构的模态计算，在简化模型过程中，需要取保合理的刚度和质量，才能保证计算精度，尤其是准确处理连接刚度是影响模态计算结果的重要影响因素。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删