1问题的提出
单纯用FEM算法建立有限元网格模型在模拟大变形问题经常会出现网格畸变,且FEM算法在模拟不连续的问题,如断裂等问题并不具有优势,SPH算法由于不用依赖网格算法,可以很好解决这一问题,但随之带来的边界难以处理,计算效率低的问题也一直难以很好解决。为此本文尝试用FEM-SPH耦合算法来耦合两者优点,以期获得理想的仿真结果。本文以单颗球形磨粒等切深划擦碳化硅工件的FEM-SPH耦合模型为例,验证这一耦合算法的高效性、正确性。
2 FEM-SPH耦合模型算例
2.1模型建立
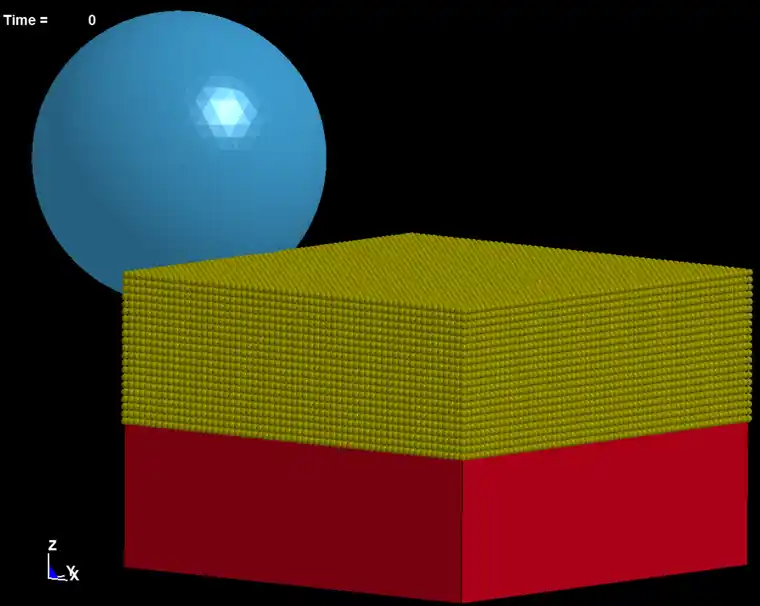
图2-1磨粒仿FEM-SPH模型
由于在磨削加工中,实际是金刚石磨粒的刀尖圆弧半径划过工件表面实现的材料去除,因此在介观尺度下,不规则形状的磨粒可以简化成球体,工件简化成与磨粒尺度相匹配的长方体,工件在7.5μm的切深范围内采用SPH算法建模,剩下部.分采用FEM算法建立有限元网格,SPH粒子总数为144000个,粒子间隔为0.25μm,SPH粒子下的FEM网格工件网格大小并不影响计算结果,为提高计算时间,可适当取大网格间距,本文中取1μm,即4个SPH粒子与1个有限元网格匹配。磨粒仿真模型如图2-1所示。几何模型的具体参数如表2-1所示。因为磨粒为金刚石材质,其硬度和弹性模量远远大于单晶碳化硅工件,因此在研磨过程中,磨粒几乎不会发生变形,因此将磨粒(密度3560kg/m3、泊松比0.2、杨氏模量1000GPa)设为刚体。单晶碳化硅是典型的的各向异性材料,本文仿真选用6H-SiC,单晶碳化硅(6H-SiC)工件的本构参数如表2-2所示。
表2-1几何模型具体参数
| 参数 | 数值 |
| 磨粒半径 切深 | 5μm 4μm |
| 工件整体尺寸 | 15×15×10μm3 |
| SPH工件尺寸 | 15×15×7.5μm3 |
| FEM工件尺寸 | 15×15×7.5μm3 |
表2-2 6H-SiC的JH-2本构参数[1,3]
| 参数 | 取值 | 参数 | 取值 |
| R(kg/m3) | 3215 | EPSI | 1 |
| G(GPa) | 193 | T(GPa) | 0.75 |
| A | 0.96 | SFMAX | 0.11 |
| B | 0.35 | HEL(GPa) | 11.7 |
| C | 0.009 | PHE(GPa) | 5.13 |
| M | 1 | BETA | 1 |
| N | 0.65 | K1(GPa) | 220 |
| D1 | 0.48 | D2 | 0.48 |
| K2(GPa) | 361 | K3(GPa) | 0 |
2.2算例实现
2.2.1选用的软件
本文为方便建模过程,采用联合建模。选用的软件有:ANSYS 19.0、WORKBENCH协同仿真平台(主要用于几何建模)、LSDYNA(用于K文件求解)、LS-PREPOST(用于模型前后处理、K文件修改、模型检查)、UE编辑器(K文件修改)。
2.2.2联合建模的单位制
全程建模均采用统一的μg-μm-μs单位制。
2.2.3建模步骤
首先,在Workbench中选用Workbench LSDYNA模块,完成磨粒和工件的有限元模型工作,建立工件时为方便后面工件的SPH粒子化及部分工件的网格划分,通过平面分割命令将工件分成两个PART,球形磨粒可以直接调用sphere命令生成。在完成磨粒和工件的几何建模后,忽略其他信息,将该模型保存为x_t格式导入到ANSYS 经典版中,继续选用ANSYS/LSDYNA模块进行单元、材料参数、网格划分工作;单元选用显示3D SOLID164实体单元,之后设置金刚石磨粒的材料本构(rigid),包括:密度、杨氏模量、泊松比;4H-SiC的材料本构选用任意一种弹性材料代替即可,后期在LSPP软件中直接修改工件的本构参数,当然也可以直接通过UE编辑器修改工件本构的关键字。在完成单元定义、材料赋予工作后,开始对磨粒和工件模型网格划分,磨粒采用四面体网格划分,网格单元大小设为1μm,工件的网格划分需要注意网格的大小。对于磨粒正下方的这部分工件,由于直接承担着磨粒的划擦作用,因此网格单元应当加密,对于下方的工件网格可以稀疏,其网格大小本质上并不会影响算例的准确性。因此,上方工件采用六面体网格划分,网格大小为0.25μm,下方网格同样采用六面体网格划分,但单元大小取大网格划分,设为1μm。网格划分完成后,可以对仿真时间、磨粒划擦速度、磨粒自由度约束、工件约束、能量控制等进行设置,也可以不设置,留在LSPP软件中对这些参数进行集中处理,这也是联合建模的最大优势所在:在联合建模中可以不必严格按照前处理→求解→后处理的CAE分析步骤进行,不必担心参数设置不全的问题。之后设置需要输出的三个物理量(能量、接触力、损伤)写出K文件完成ANSYS经典界面下的分析过程。然后在LSDYNA的LS-PREPOST前后处理模块打开保存的K文件,进行网格化工件的SPH替换、工件材料的替换、接触约束边界条件的设置等操作。对于SPH工件的转化一定要注意实际建模尺寸与转化成SPH尺寸之间的对应关系,在选用Solid Nodes SPH创建方法时,实际建模尺寸与SPH尺寸之间是对应相等的(本文选用此种方法创建SPH粒子),而在选用Solid Center方法创建SPH粒子时,转化后的SPH粒子总长度是要小于实际建模尺寸的,这是由于Solid Center是将每个网格的中心点转化为一个SPH粒子,这可以理解成每一个网格都简化成一个具有网格质量位于网格中心的理想质点,因此网格转化成点,在尺寸上就减少了一个粒子间隔长度。因此,选用Solid Nodes方法创建上方SPH工件,下方网格工件保留不作处理。之后设定SECTION-SPH关键字,选用材料模型MAT 110(JH-2),设定材料模型所需参数,并将材料关联到工件Part;之后设定DEFINE-CURVE 关键字定义磨粒轨迹与速度并关联到rigid Part部分。对磨粒的约束通过PRESCRIBED_MOTIOM_RIGID关键字定义,较为简单,而对FEM-SPH耦合工件的接触设置用固连点面接触(TIED_NODE_TO_SURFACE)定义,这就避免了单纯SPH工件需要定义关键字*BOUNDARY及 SPH_SYMMETRY_PLANE来对边界处粒子进行约束。本文的FEM-SPH耦合之处除了工件之间的耦合,还有磨粒与SPH工件的耦合,对对磨粒与SPH工件的耦合接触采用AUTOMATIC_NODES_TO_SURFACE 关键字进行定义。最后,对仿真时间、沙漏能等进行最后的设置,另外对于工件损伤裂纹的查看需要借用UE编辑器修改EXTENT_BINARY关键字完成,将所有已经定义的关键字在 Part 中进行关联后,并用UE编辑器最终检查K文件后,完成球形磨粒划擦6H-SiC工件算例。
2.2.4求解算例
最后在LSPP将文件保存为K文件格式,用LSDYNA Solver求解器求解K文件。在LSPP中可以打开binary文件(D3PLOT)查看云图,绘制二维图像等。
3 FEM-SPH、SPH对比
仿真效率的高低与电脑的配置有关,本次算例在如图3-1所示的电脑配置下进行。为了较为客观比较采用FEM-SPH算法与采用SPH算法建模的计算效率,本文进行了两次仿真,仿真参数及几何模型尺寸均设为相同,但采用SPH算法建模的计算效率低下,在设置相同仿真时间1μs时,计算时间实在太长(>90h),因此经过多次仿真调试试验后,在设置仿真时间为0.04μs时,采用SPH算法建模的计算时间约为14h37min,这比仿真1μs,采用FEM-SPH算法建模的计算时间(10h42min)还要长(如图3-2所示),由此可见,采用FEM-SPH算法的计算效率要远远高于采用SPH算法建模的计算效率。
图3-1电脑配置
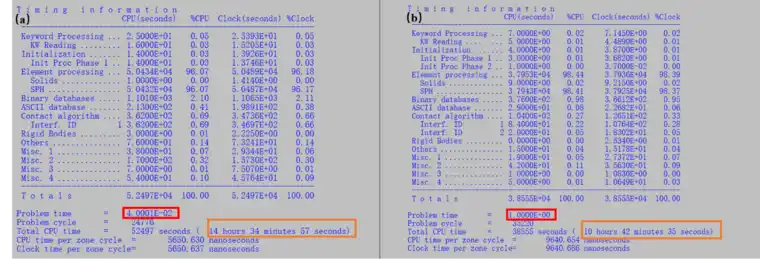
图3-2不同算法计算时间对比
4分析与讨论
4.1接触反力分析
在ANSYS对模型进行前处理时定义输出 RCFORC,即可用 LS-PREPOST 提取出单颗磨粒在等切深刻划过程中受到的切向力、法向力和轴向力。三向接触力如图4-1所示。分析:Y-force从磨粒进入工件开始一直在0上下波动。这是由于Y向与加工方向垂直;X、Z-force从磨粒进入工件后数值急剧上升到30mN、50mN,但Z向力更大,且在t=0.3μs后,Z、X向力出现波动,呈现先减小后缓慢增大再减小的波动,且X向力方向为负,但t=0.8μs后,三向力都可以减小。这是由于磨粒与工件接触面积逐渐增大,受力面积增大,磨粒不断压迫(斜向下)工件破碎,法向力也就不断增大,而切向力由受力分析可知其方向始终与磨粒刻划方向相反,即为负值。t=0.8μs后磨粒逐渐离开工件,所以力值逐渐变小。
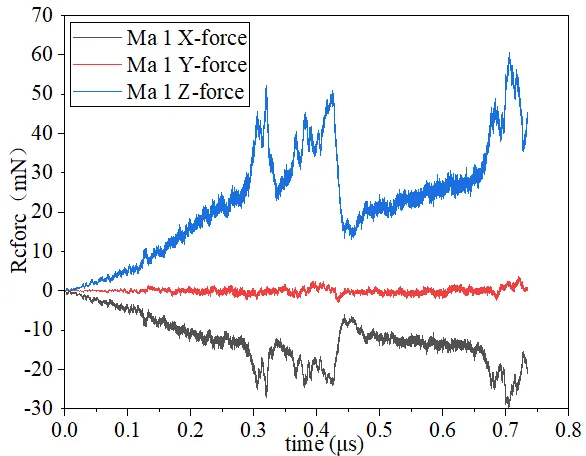
图4-1三向接触力分析
4.2能量分析
在LSPP中通过定义matsum可以查看SPH工件(PART 4)的能量变化。SPH工件的内部能量随时间的变化关系如图4-2所示。由Griffith[4]提出的断裂能量分析可知:球形磨粒在开始与工件接触后,材工件内部能量迅速增长,形成尖峰,表明在研磨初期,磨粒能量完全被工件吸收且工件没有对外做工,因此表现为塑性变形,没有损伤和脆性断裂出现,之后工件能量急剧下降,表明此时脆性断裂出现,能量释放转化为磨屑动能、工件变形能、工件表面自由能、热的形式。
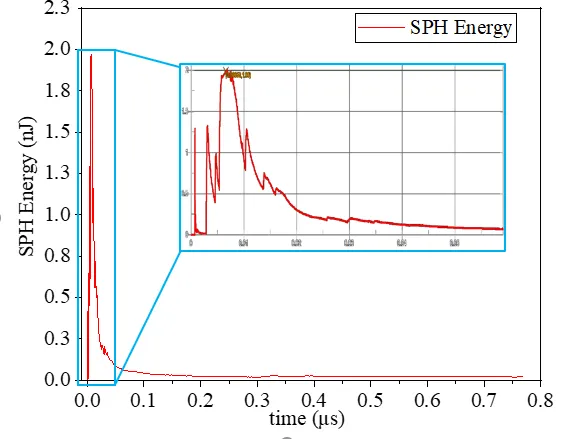
图4-2 SPH工件能量变化图
4.3最大等效应力
图4-3表示划擦过程中不同时刻的等效应力折线图。分析:比较大的应力值主要集中在划擦的初始阶段。可以发现等效应力的趋势与三向接触力的趋势有一定的对应性。当 t=0.076μs 时,也就是塑脆临界共存态到脆性模式的转变点,应力值急剧上升到12.2Gpa,然后持续上下震荡,在t=0.4μs、t=0.7μs左右时,最大应力值出现尖峰,这与三向接触力变化趋势相对应,在此时法向力、切向力以及轴向力(轴向力在0左右波动)达到相应最大值。
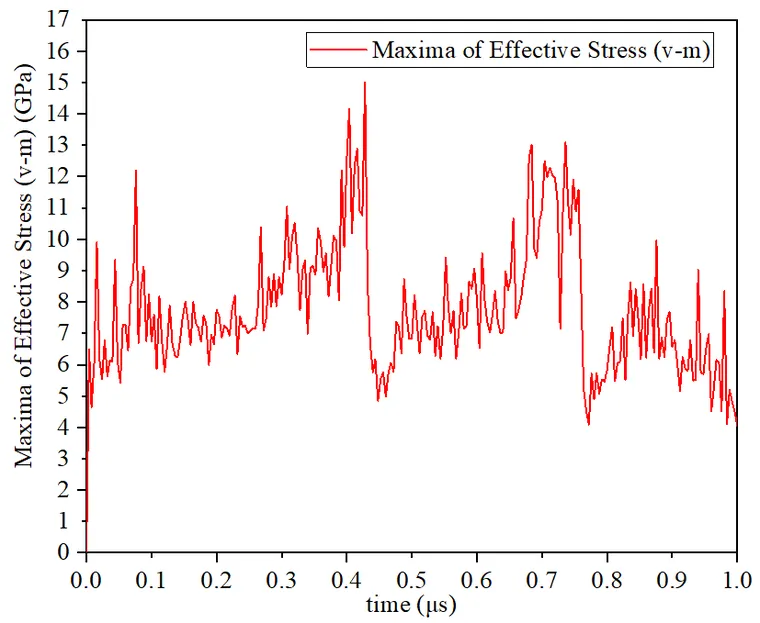
图4-3最大等效应力
4.4材料去除状态分析
球形磨粒在研磨加工硬脆工件时,一般是以脆性断裂的形式去除材料。图4-4分别给出了在相应时刻的塑性应变、等效应力图。可以看出磨粒正前方45°范围内所受应力最为严重,也就意味着工件在这一范围内最容易产生损伤堆积,同时磨粒以粉末状飞溅去除与实际加工单晶碳化硅工件相一致,也初步验证了仿真结果的正确性。而从磨粒对SPH工件的三向压力来看工件损伤区域的方向更为直观,如图4-5(a-c)所示,通过FCOMP→Misc→history#2可以看裂纹损伤情况如图4-5(d)所示。

图4-4应力应变图
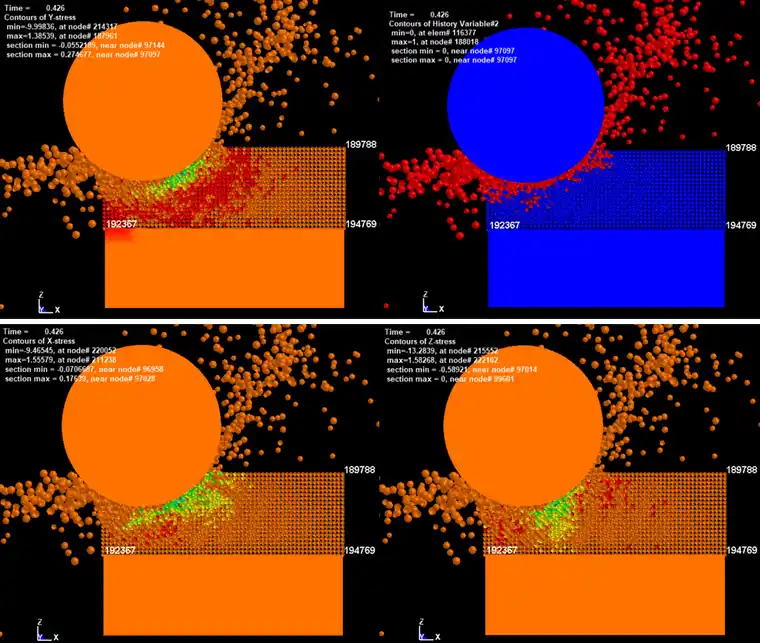
图4-5X Y Z向磨粒对SPH工件的压力显示云图(a-c),SPH工件损伤图(d)
5 总结
经多次调试与仿真实验,得出结论:
1)计算效率方面:发现其计算时间比单纯用SPH快了16倍(SPH算法耗时约16小时,而采用FEM-SPH耦合算法仿真耗时1小时13分钟左右),仿真结果文件D3PLOT文件平均十秒一个,仿真过程极度丝滑。
2)SPH边界难以处理问题:FEM-SPH耦合模型不用考虑用虚粒子约束法定义SPH边界,在耦合模型中直接将外层SPH粒子固连在FEM网格上即可。
因此,采用FEM-SPH耦合建模同时避免了单纯S9PH算法的边界难以处理、FEM网格算法难以处理大变形的两个棘手问题。这为金属切削、磨削加工、研磨抛光加工过程的仿真提供了一种更加高效的仿真手段,具有一定的理论与实践意义。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删