ANSYS/LS-DYNA SPH-FEM耦合拉伸模拟实战

1、背景

有限元方法作为数值计算的强大工具，计算结果精确且可重复，降低了试验成本，缩短了研发周期，但有限元方法在切削仿真时容易造成网格畸变，造成求解中断。

光滑粒子动力学（smoothed particle hydrodynamics，SPH）的基本思想是将连续体离散为相互作用的粒子，每个粒子具有密度、质量以及相关物理属性，粒子间运动遵循牛顿第二定律；其本质是一种拉格朗日方法，运用插值理论将宏观变量（如压力、密度以及温度等）一系列无序点的值通过微分形式转换成积分运算。SPH法采用粒子划分，不依赖于网格，具有很好的自适应性，可以避免网格畸变，适合切削引起的大变形问题。然而SPH法对每个粒子进行计算时，需要搜索影响区域内近邻的粒子信息、粒子物理量计算和搜索信息都比较费时，因此计算效率比普通的有限元法低，对于三维模型占用计算机资源较大。

针对SPH与FEM的各自特点，为提高计算效率并消除网格畸变，采用SPH与FEM耦合的方法解决切削数值模拟问题。在变形大的区域采用SPH，避免FEM的网格畸变过大造成计算困难。在变形小的区域采用FEM，以提高计算效率。SPH与FEM耦合算法分为固定耦合算法和自适应耦合算法。固定耦合算法在计算之前就已确定SPH区域和FEM区域。自适应耦合算法则在计算之前都是FEM网格，在计算过程中自动地将大变形的有限元网格单元转换为光滑粒子，并按SPH法计算物理量。

基于以上考量，本文运用ANSYS/LS-DYNA进行了SPH-FEM耦合算法的拉伸试验模拟。

2、模型设置

分析模型如下图所示，拉伸件两端采用壳单元，中间段采用SPH粒子法划分。粒子与壳单元接触段采用tie功能进行绑定，以实现FEM与SPH之间的耦合计算。

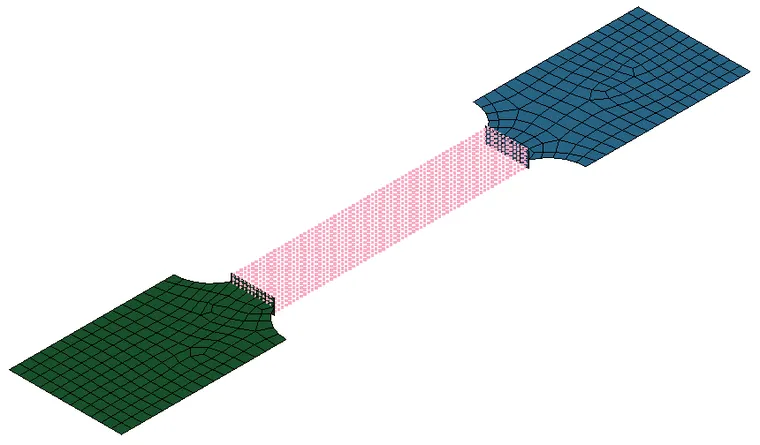
由于采用了耦合算法，还需要对壳单元和SPH粒子进行相关的设置，具体内容如下：

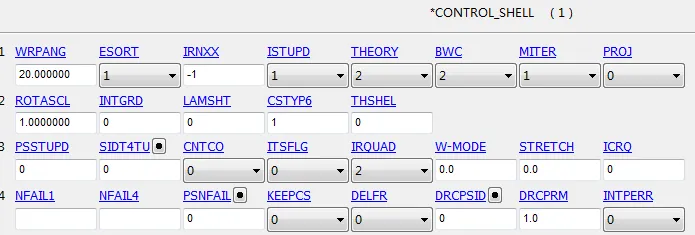
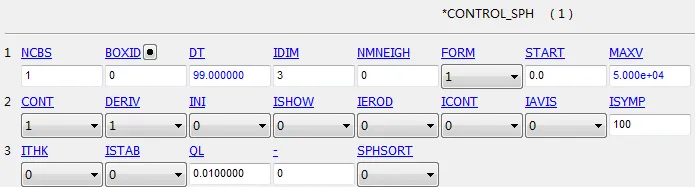
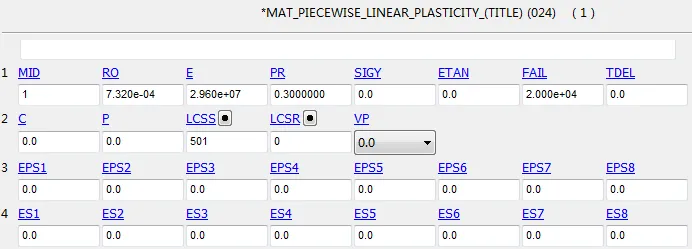
对于模型的材料设置，考虑到模型的形状，断裂破坏肯定会发生在中间粒子区域，而模型的两端壳单元区域属于加载区域，不会发生破坏，也不是本次模拟的关心区域，因此为了进一步提高求解效率和节约求解资源，模型将壳单元区域赋予刚体材料模型，即不考虑模型两端的变形情况。粒子区域的具体材料参数如下图所示：

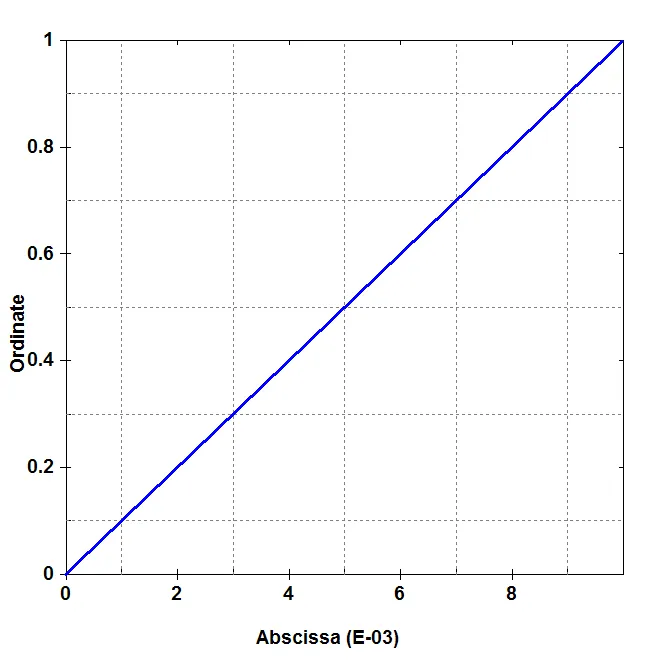
为模拟拉伸工况，本次模拟中将模型的一端壳单元的自由度全部约束，使其成为固定端，在另一端壳单元采用线性位移加载，加载曲线如下图所示：

除此之外，还需要设置相关的输出，计算终止时间等内容，在此不进行一一赘述。模型摄制完成之后即可导出K文件，利用ANSYS/LS-DYNA求解器进行求解。

3、结果分析

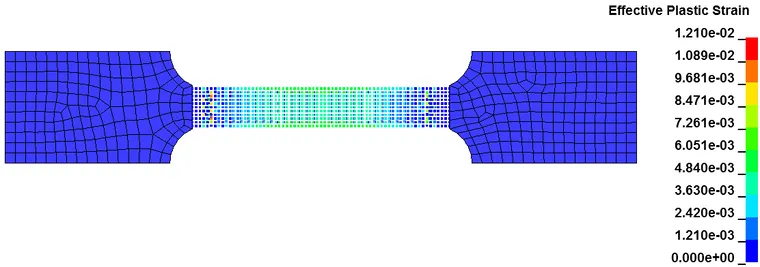
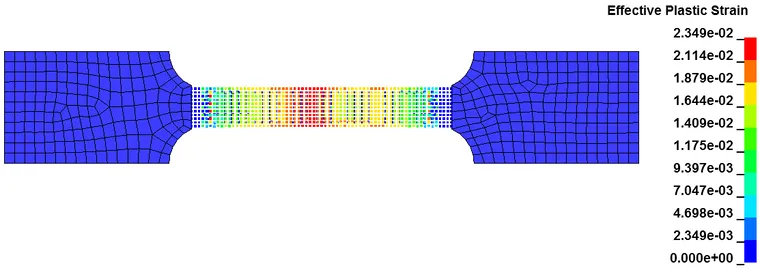
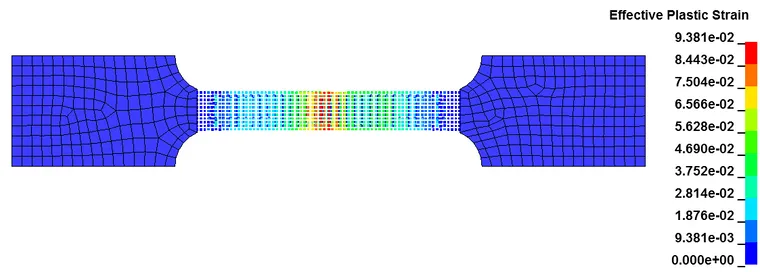
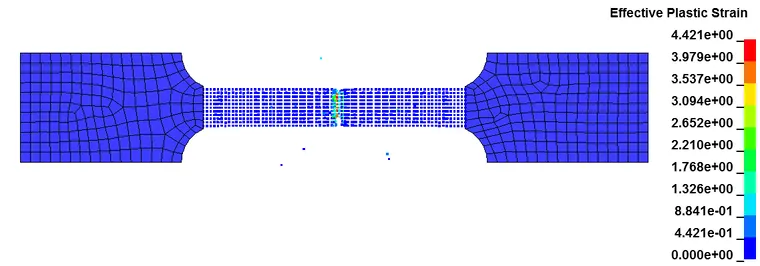
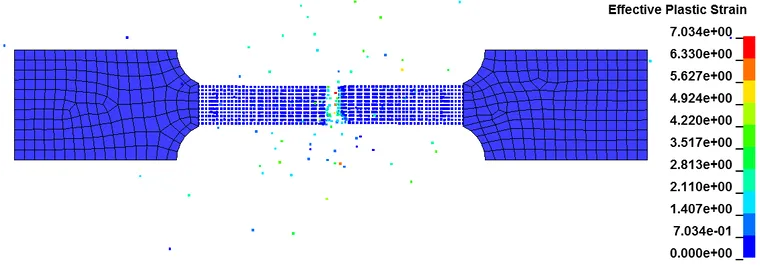
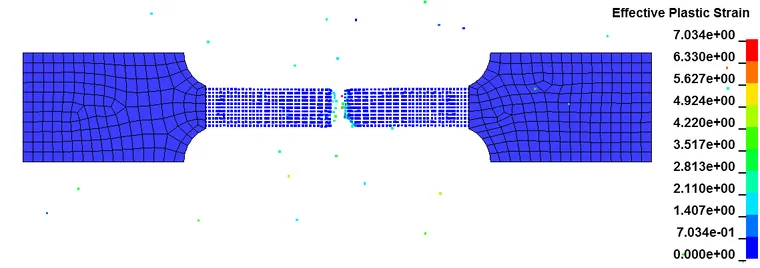
以上为拉伸件的塑性应变随时间的分布图，可以看出断裂发生在预期位置，证明了采用SPH-FEM耦合方法进行联合仿真是可行的。SPH-FEM耦合的方法，吸收了FEM法计算效率高和SPH法模拟大变形能力强的优点，可以为大变形的材料仿真如切削等提供一种高效、准确的途径。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删