1工程背景
无论是在军事还是民用领域,爆炸都有着极为广泛的应用,如东风导弹部队的战斗模拟、金属爆炸成型等。目前,对于爆炸动力学研究一般有两种方法,即实验与仿真。爆炸实验模拟是对爆炸精确分析的较好手段,但通常成本高,花费精力大,用仿真的手段对爆炸过程进行模拟,拟合仿真数据与前人实验结果比对验证,也是获得较为准确可靠的数据。对于爆炸过程模拟的常用方法有公用节点算法、接触耦合算法及流固耦合算法等。但考虑到后两种方法的计算时间较长(ALE算法计算效率较低)[1],同时,本文经过多次仿真调试发现:流固耦合算法所得到的的计算结果对控制参数的取值十分敏感,得到的数字结果差距很大。因此,本文采用共节点算法来模拟炸药在混凝土中的爆炸过程。
2模型建立
2.1模型分析
本文设想是将炸药放入混凝土中心位置进行起爆,因此炸药和混凝土整个模型可以看成是一个完全对称的模型,因此,本文建立1/8模型,将炸药单元建立在模型中心位置。炸药单元与混凝土结构之间共节点算法定义连接。对于网格划分,炸药单元网格划分密与混凝土结构。被爆炸物尺寸社设为1m3的立方体块,炸药尺寸较小,设置为5cm3的立方块,简化模型如图1所示。

图1共节点算法爆炸有限元模型
2.2炸药、混凝土本构模型
炸药本构采用LSDYNA提供的8号高爆炸药本构模型*MAT_EXPLOSIVE_BURN,同时使用JWL状态方程模拟炸药爆炸过程中的压力与体积的关系。炸药本构参数和JWL状态方程参数分别如表1、2所示。被爆炸物为混凝土材料,选用111号材料本构。
表1 8号炸药本构参数
| /kg·m-3 | D/m·s-1 | PCJ/Pa | BETA | K | G | SIGY |
| 1.631e3 | 0.6718e4 | 0.1852e11 | 0 | 0 | 0 | 0 |
表2 JWL状态方程
| A | B | R1 | R2 | OMEG | E0 | VO |
| 5.409e11 | 0.094e11 | 4.5 | 1.1 | 0.35 | 0.08e11 | 0 |
2.3ANSYS LSDYNA源程序建模生成K文件
因为模型较为简单,直接在ANSYS LSDYNA中建立几何模型并进行前处理操作,本文使用图形交互环境建模,熟练者也可以直接使用APDL语言建模。为避免建模尺寸混乱,本文选用的单位制为国际单位制,在完成工程属性的相关定义后,开始定义变量、单元类型、材料和实常数,被爆炸物的材料本构可以先任意设置一种弹性本构材料,后处理可以手动修改K文件添加上被爆炸物的混凝土本构关键字及参数。最后建立实体模型采用自下而上的建模法,先建立点在建立线最后形成面。实体模型完成后开始划分网格,建立有限元模型,被爆炸物的网格次尺寸为1/17m,炸药网格为0.025m大小。接着开始定义初始条件与边界条件,对于边界条件的设置本文建议直接在ANSYS中完成,虽然在LSPP中也可以实现,但很繁琐不及ANSYS来的快捷方便。在ANSYS中实现边界条件仅6行代码如下:
!NSEL,S,LOC,X,
DSYM,SYMM,X,
Nsel,s,loc,Y,
DSYM,SYMM.Y,
Nsel,s,loc,Z,
DSYM,SYMM,Z,
最后定义求解参数,计算终止时间设为0.8ms,其他设为默认,直接写出K文件,保存为1.k。
2.4修改K文件并求解
炸药材料本构关键字需要手工修改,用UE或者LSPP打开L文件,本文直接使用UE修改K文件。首先用UE打开K文件,然后使用搜索功能,找到MAT,将炸药关键字及参数替换掉预设的弹性本构材料,并按照表1和表2参数写入JWL状态方程,赋予炸药PART上,将文件命名为explode.k,这样K文件完成修改。
2.5求解
求解可以用ANSYS求解也可以用LSDYNA求解器求解,均可。
3 LSPP后处理
3.1等效应力云图
由于爆炸时间极短,本文选取#STATE 1 3 4 5 6 7状态的爆炸点应力云图变化情况如图2所示,可以看出在起爆瞬间,爆炸边缘处的混凝土结构就出现破裂痕迹,炸药边缘处应力集中明显,破碎沿着边缘处不断延伸直至撕裂开来。而随着爆炸能量的瞬间集中释放后,本文截取#STATE 20 22 24 26 28 30状态来表示混凝土在爆炸后的表面应力情况,如图3所示。可以看出应力开始减小,中间起爆处撕裂现象渐渐成型,不在继续向外扩展。

图2起爆瞬间应力变化

图3 起爆后表面应力变化
3.2表面损伤
在LSPP中定义输出变量为vary#2,可以看损伤云图如图4所示。其基本与应力云图变化一致,通过损伤云图,可以通过图像处理的方法来准确计算出整个表面的损伤情况占比,这是损伤云图的一个巨大优势,但由于需要图像识别相关技术,本文只从云图表现特征简要分析。
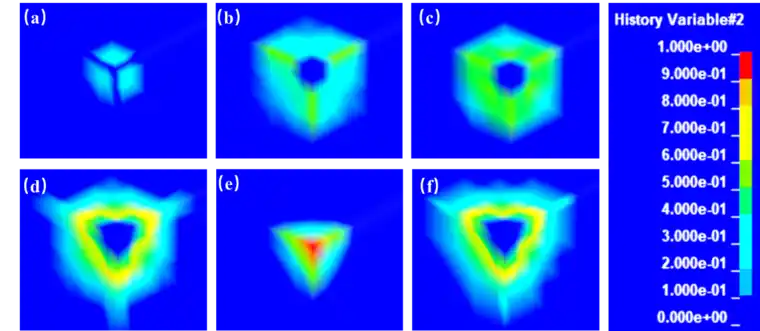
3.3其他后处理
其他后处理,如最大等效应力曲线绘制,内能动能变化曲线等都可以通过LSPP软件进行提取与二次筛选,本文着重爆炸模型的共节点算法的实现,对LSPP中众多后处理功能的实现需要进一步挖掘。
4结论
1)实际上,不管是采用何种算法进行爆炸模拟分析,在每一种算法中都有多个控制选项,其参数的不同取值直接影响计算结果。因此仿真结果应当结合实际,以实验为基础在调整参数。使仿真结果与实验匹配,这样的仿真结果才有可信度。
2)爆炸模拟分析的精度依赖于材料本构、状态方程等参数的合理设置,因此参数设置的合理性影响仿真精度。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删