1引言
EFG方法与SPH方法相比具有较好的协调性及稳定性,比FEM方法具有更高的精度和收敛速度,而且没有体积锁死现象。因此,本文尝试采用EFG算法进行圆形铜柱Taylor冲击测试仿真,对圆形铜柱Taylor冲击测试实验具有一定的实践指导意义。
2 EFG算法
2.1无网格伽辽金算法(EFG)
无网格伽辽金方法(EFG)最早于1994年由美国西北大学Belytschko T教授提出,属于无网格算法中的一种。
2.2数值求解流程
由EFG算法的基本原理及主要软件操作步骤,查阅相关无网格法书籍和关键字文件,总结出采用EFG算法的数字求解流程如下,流程图如下图1所示。
1)根据分析对象的形状布置节点和边界,并将分析对象所在空间划分背景积分网格,在背景网格内布置高斯积分点,记录下高斯积分点的位置和积分参数。
2)在每步计算中,完成以下步骤:
1)扫描高斯积分点,如果高斯积分点在分析域内,则执行步骤2) ~4)。
2)根据高斯积分点的坐标以及该高斯积分点的影响半径,找到位于该高斯点影响域内的所有节点。
3)根据高斯点和影响域内节点的坐标进行最小二乘运算,得到形函数矩阵以及形函数矩阵的导数矩阵B。
4)计算并存储该高斯积分点的刚度矩阵和载荷向量。
5)集成并求解整体刚度方程,得到位移向量u'
6)根据1',由最小二乘法拟合出节点的真正位移u。
7)计算积分点的应变、应力等。
3)更新节点位置和边界位置,重复执行步骤(2),直至计算结束。
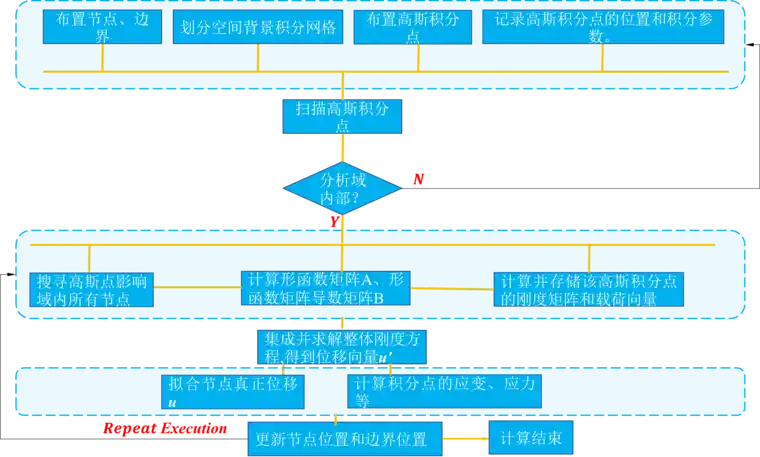
图1 EFG算法实现流程图
3圆形铜柱Taylor冲击计算模型
3.1基本建模流程
在WB LSDYNA中建立圆柱的几何模型(WB LSDYNA只在ANSYS19.0版本及以上才有,本文选用的版本为ANSYS19.0),圆柱底面半径设为5cm,圆柱高度设为50cm。圆柱材质为铜,铜柱材料模型为*MAT PLASTIC KINEMATIC,铜柱的材料参数见3.2关键字所示。约束及初速度设置:铜柱除底部节点设置为全约束外(关键字*SPC_SET),所有节点具有负Z方向初始速度200m/s。计算时间为0.9ms,整个冲击测试模型采用EFG算法(*Solid_EFG)进行计算,本文建模不考虑热力学因素,故建模单位采用国际单位制kg-m-s,计算模型如图2所示。在WB LSDYNA中完成上述设置后,继续在ANSYS LSDYNA中进行模型的前处理,设定单元为实体三维显示SOLID164单元,由于铜柱材料参数设置较多,可以先任意设置一种弹性材料,只要保留材料的关键字即可,后面在LSPP中替换材料本构。网格划分大小为5mm,在完成这些操作后忽略所有警告,直接写出K文件进入LSPP中进行节点速度(200m/s)、底部节点全约束、EFG单元替换、材料替换、仿真时间设置操作,最终完成的K文件导出命名为2.k,见附件。本文建模方法采用的是联合建模技术,步骤较多的同时却大大方便了软件操作,灵活性更强。

图2计算模型
3.2使用的相关关键字
$EFG计算控制,采用默认值,核函数选项为立方样条函数

0 0 12
$输出控制
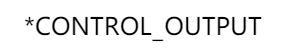
0 0 0 0 0 2 1000
$计算结束时间

0.00090000
$能量信息输出
*DATABASE_GLSTAT
0.500000
$材料信息输出
*DAIABASE_NODOUT
0.500000
$结果数据输出时间间隔
*DATABASE_BINARY_D3PLOT
5
0
$BOX方式定义初始速度
*INITIAL_VELOCITY
0.000 0.000 1
0.000 0.00 -200
$定义BOX1,包括除底部节点外的所有节点
*DEFINE_BOX
$PART定义
*PART
1 1 1
*SECTION_SOLID_EFG
1 1 41
1.3 1.3 1.3
$铜柱采用弹塑性材料本构
*MAT_PLASTIC_KINEMATION
1 8930.000 1.170000e11 0.350000e6 0.004000e6 0.001000e6 1.000000
0 0 0 0
*ELEMENT_SOLID
*END
3.3后处理显示
本质上,EFG和FEM两种算法共享同样的数据库,因此采用LSPP读入2.k结果文件后,将FEM网格显示为EFG质点时,可以通过Page1的Appear按钮选择Pick Part,之后更改显示方式为Sphere,点击AIIVis,Done就可以显示EFG粒子,此外,可以使用Setting按钮调整质点的显示效果,如图3所示。
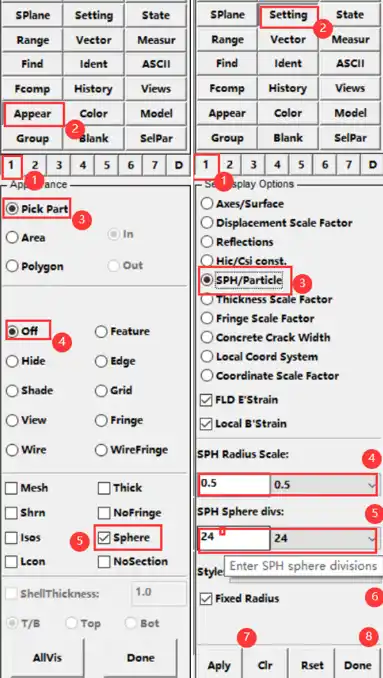
图3 EFG实体粒子后处理显示
4结果分析
4.1等效应力
铜柱经过高速-z向的冲击后,从各个方向的等效应力云图(如图4所示)来看,被冲击铜柱底面圆圈外侧发生变形最为严重,表现为底边铜片被快速压扁后向四周扩散,并发生边缘翘曲(如图4(d)所示);而从上往下的俯视图来看(图4(a)),铜柱远离底面的部分中心圈内变形不大,由于底部被约束,底部中心圈变形最大,但中心圈外圈受力要大于内圈(如图4(b)所示);从图4(c)明显可以看出被约束的粒子变红(承受大应力)。

图4(a)俯视图

图4(b)仰视图

图4(c)左视图
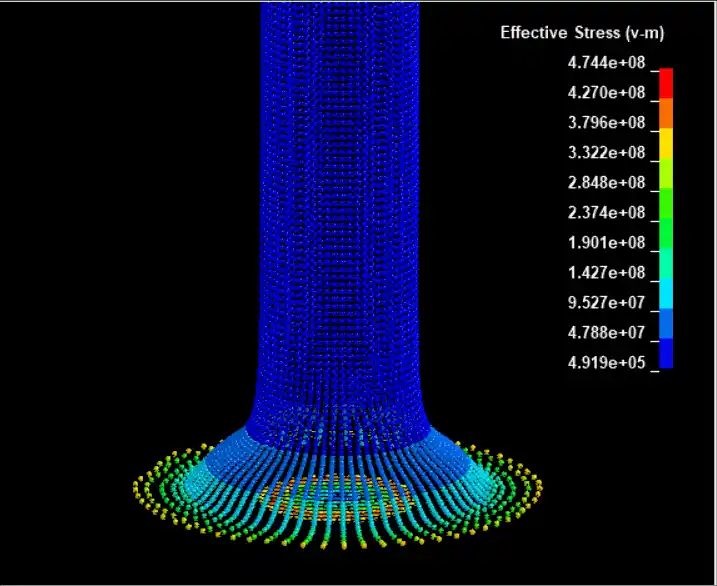
图4(d)三维图
4.2等效应变
等效应变图如图5所示。应变过程可与等效应力一一对应起来,不同之处在于t=0.85-0.90ms时(冲击末期),铜柱底面中心圈内并不是最大应变处(如图5(b)所示),这与图4(b)不同。
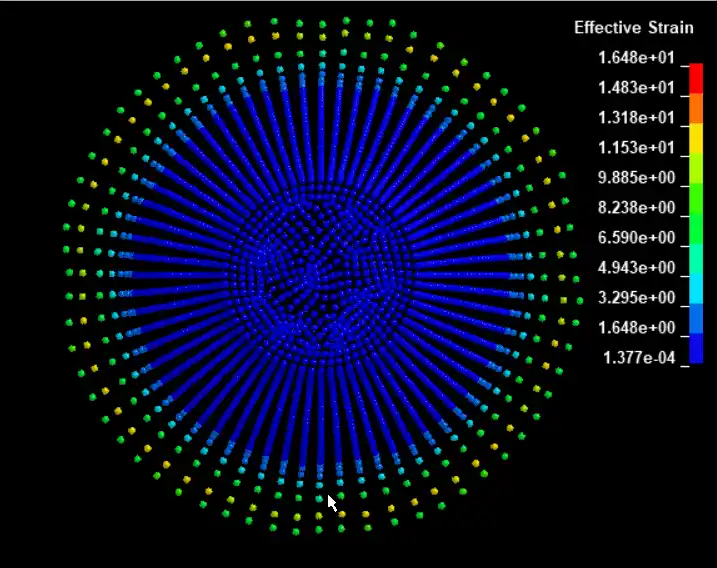
图5(a)俯视图

图5(b)仰视图

图5(c)左视图
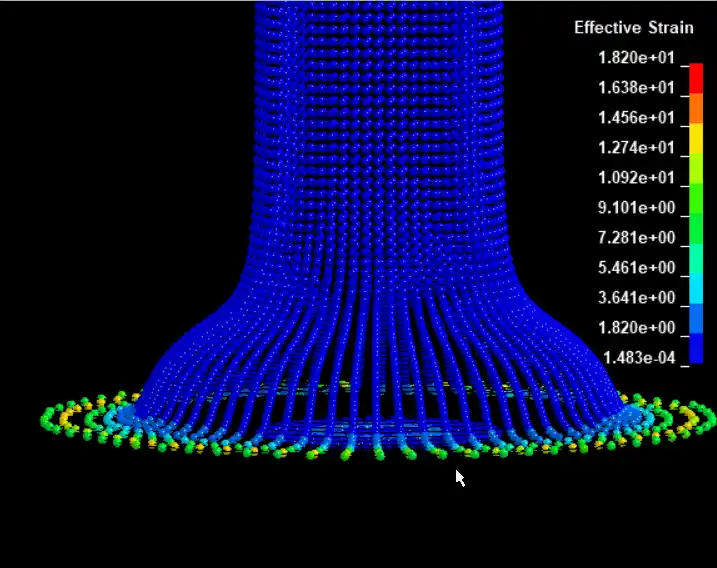
图5(d)三维图
4.3加速度
从加速度的角度可以可以分析铜柱在冲击瞬态的动力学变化过程,在XYZ三个方向上的加速度变换云图如图6所示。可以看出不管哪一个方向,加速度的变化都是呈现对称变化:X方向:左右对称(红、蓝左右对称,按图示方向),Y方向:上下对称(红、蓝左右对称,按图示方向),Z方向:圆形对称(红、蓝左右对称,按图示方向)。在LSPP中可以提取铜柱在XYZ方向的加速度数据,可以定量反映加速度变化情况,如图7所示。可以看出XYZ向的加速度是关于0线对称波动变化的,这与云图表现形式一致,另外,加速度在波动变化中最终趋于0,这是由于底部的全约束导致的。
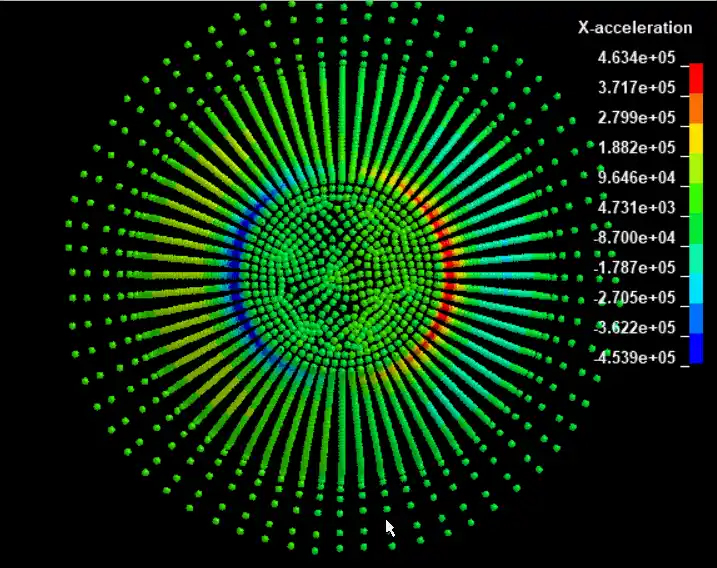
图6(a)X方向加速度

图6(b)Y方向加速度
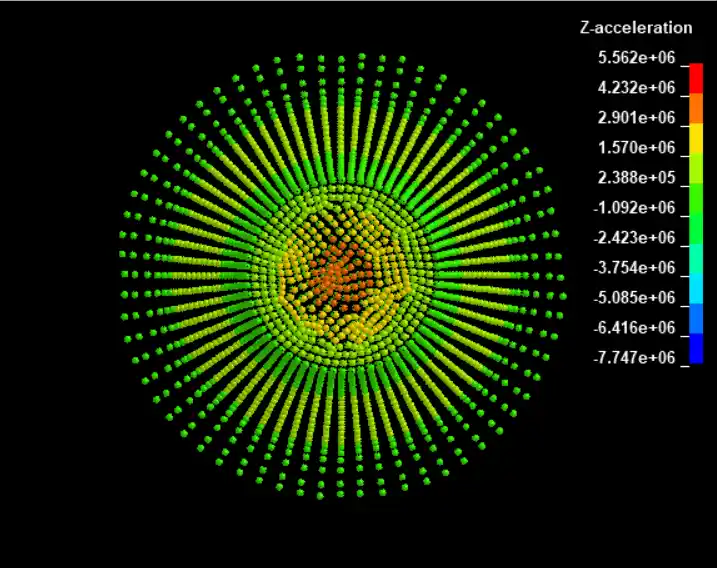
图6(c)Z方向加速度
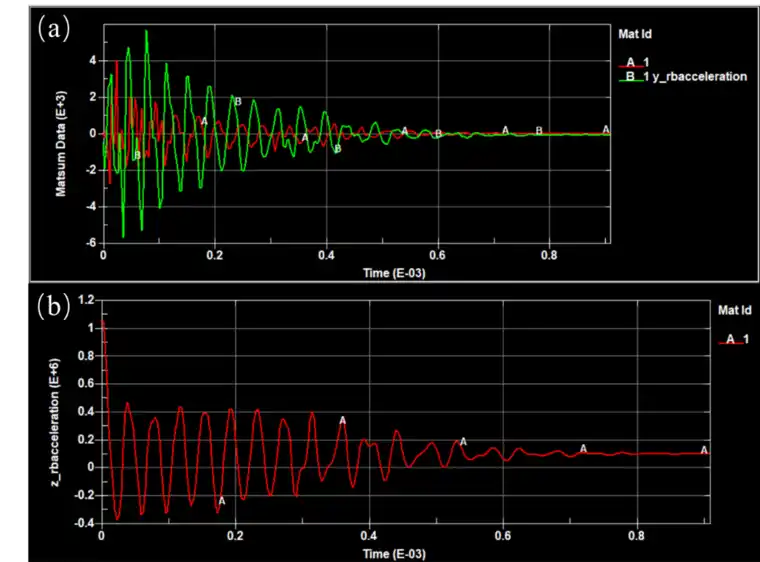
图7 加速度变化曲线
4.5能量
从图8(b)可以看出在冲击过程中,能量是守恒的,由于底部的约束,动能在不断变小,而铜柱的内能因此不断变大,整体的能量是守恒的,因此动能、内能曲线相加于一点。而从铜柱整体的动能-内能变化曲线(如图8(a)所示)中(对应LSPP中matsum中21号关键字),不断出现的波峰表示铜柱的变形不断加重,波峰数值逐渐降低,表明铜柱的变形速度变慢,最终波峰变成一条直线表明变形停止,能量降为0(几乎为0),能量以摩擦、热等形式散失。
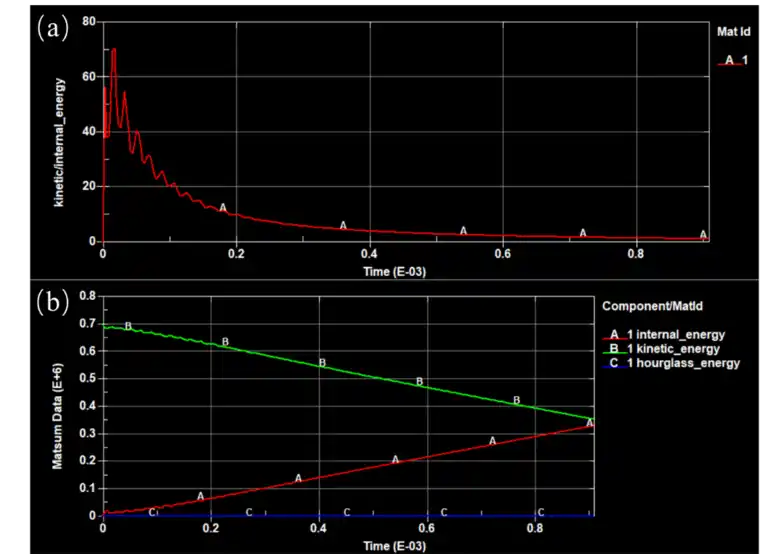
图8 能量变化曲线(a)铜柱内部动能-内能变化曲线图(b)整体能量守恒变化曲线图
5结论
1)EFG方法比FEM方法具有更高的精度和收敛速度,没有体积锁死现象。但同时EFG方法计算量要比FEM方法大得多,且还必须借助背景网格进行数值积分才能进行计算(下图中黑色线体部分是背景网格)。
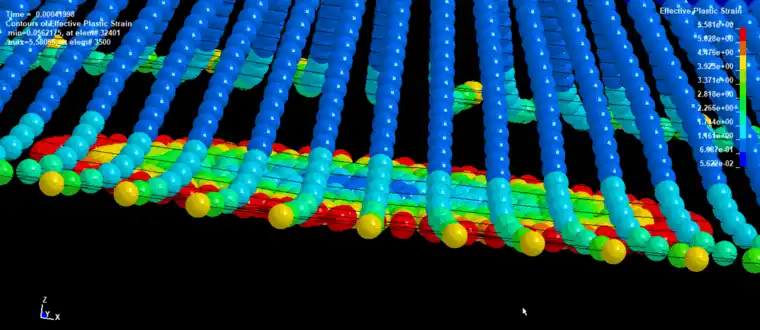
2)为节省计算时间,可以建立圆柱形铜柱的四分之一模型,计算模型设置关于YOZ和XOZ平面对称,进行Taylor冲击测试仿真分析。
3)EFG方法目前的理论部分还不够完善,这也是无网格法包括SPH法的薄弱点,想要得以推广还得不断完善底层理论。需要注意的是:在EFG算法中,计算时为确定EFG PART,对于三维问题,需要使用六面体单元作为背景网格;对于二维问题,需要使用四边形单元作为背景网格。
4)本文并未进行铜柱的Taylor冲击测试实验,将实验结果与仿真结果对比分析会更加具有说服力。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删