1背景及意义
利用LSDYNA进行跌落分析计算是其在民用领域的重要功能。比如常见的家电抗震性能测试、冰箱跌落等。从底层算法上来讲,冰箱跌落、家电产品跌落抗震性测试在软件操作技术上都是相通的,这都可以看成一个物体从一种介质落入另一中介质中。因此,本文从最简单的矩形金属板跌入水中来探索跌落仿真模拟的实现,这对于理解跌落分析的软件操作实现具有一定的实际意义。
2有限元模型的建立
2.1模型描述
金属板在距离水面0.1m的高度以50m/s的速度下落,金属板、空气域及水域的尺寸如图1所示。
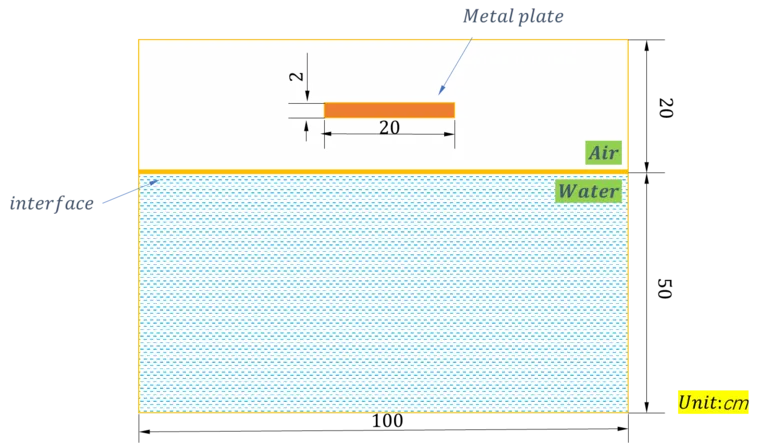
图1模型示意图
2.2ANSYS LSDYNA建模分析
由图1可知,本文的跌落模型由水介质、空气介质、金属板三个部分组成,水和空气属于常见的流体,因此并不适合采用拉格朗日网格建模;另外由图可知金属板与空气、水的交界面需要采用耦合算法,模型中空气和水域周边采用映射边界条件,另外本文假设水域无限大,那么本文模型就可以采用单层实体网格建模以减小计算量同时可以充分利用LSDYNA中的多物质ALE算法。由于模型尺寸为cm尺度,故单位制选用cm-g-μs单位制。模型各个部分采用的算法及单元赋予如表1所示。
表1 算法及单元赋予表
| PARTS | ELEMENTS | ALGORITHM | MATERIALS |
| Air | SOLID_ALE | ALE | NULL |
| Water | SOLID_ALE | ALE | NULL |
| Metal Plate | SOLID | LAGRANGE | JHC |
3算例求解
3.1 ANSYS求解
本文所用软件为ANSYS 19.0经典版,模型的建立、空气、水、金属板的材料赋予都是在ANSYS LSDYNA经典版中完成,由于ansys中并没有多物质耦合ALE单元的定义,故可以先只设置三维实体SOLID164单元,之后在LSPP中进行替换。这种思维在进行ANSYS与LSDYNA联合建模时候经常用到。之后对空气水及金属板进行网格划分操作,空气及水的网格单元大小设置为1,金属板的网格单元大小设置为2即可。由于ANSYS进行约束定义、节点组定义相当繁琐,故对约束、节点组的定义放置在LSPP进行设置。那么在网格划分完成后直接可以设置求解时间为5e-3,之后进行能量控制选择(选择默认),时间步输出为10微秒一个,最后输出K文件。
3.2 LSPP求解
将上一步骤输出的K文件导入到LSPP中进行再处理,对约束及节点组进行定义。作者认为处理流固耦合相关问题,用ANSYS和LSPP联合处理约束、网格划分、节点组定义、流固耦合问题更加方便高效。原因:ANSYS建模并不能直接生成耦合算法所需要的*SET_SEGMENT组件,那么只能通过“借用定义法”定义NON_REFLECTION的办法来生成*SET_SEGMENT组件,这样就显得繁琐臃肿,因此对于这一块的设置完全可以用LSPP处理,在LSPP中直接找到相关关键字进行编辑就可以快速完成流固耦合的相关定义,其对于流固耦合的理解性更好,但缺点在于需要在LSPP中进行第二次关键字处理。
3.3求解
在进行最后的约束节点组定义后检查K文件无误后即可存盘,在LSDYNA SOLVER中进行K文件求解。
4后处理
4.1 浪花形成过程的动态显示
选择主菜单区域Fcomp>Misc>Species Mass Mat#1,单击Apply按钮,播放动画得到的金属板落入水中激起的浪花现象如图2所示。图中可以看出仿真得出的浪花与实际较为相符贴合。

图2浪花动态显示
4.2金属板下落过程中的速度变化
图3给出了在不同关键时刻金属板的速度变化情况。
图3(A)表明:在金属板刚刚进入水面(刚刚离开空气),金属板是以5*e-3cm/s的速度向下运动,而在金属板已经进入水中的瞬间(图3(B)所示),金属板左端速度依顺时针变化,右端速度依逆时针变化,速度大小从左右端点向外增大扩散,金属板(除去端点效应)击打水面,因此激起水流也向外圆周扩散;
在此后这种扩散趋势没有明显变化(如图3(C)所示),但速度值逐渐增大,这是因为金属板不断击打水面,水的动能增加,速度因此增加;图3(D)可以看出明显的金属板击打水面引起的浪花现象;
随着金属板跌落水面深度增加,被激起的浪花按照速度变化的方向,在浪花末端呈“卷起”状(如图3(E)所示),这与现实生活中浪花的打卷现象也是相符的,而由于空气域的边界定义较小,浪花开始向空气域左右两边扩散(溢出)如图3(F)所示。
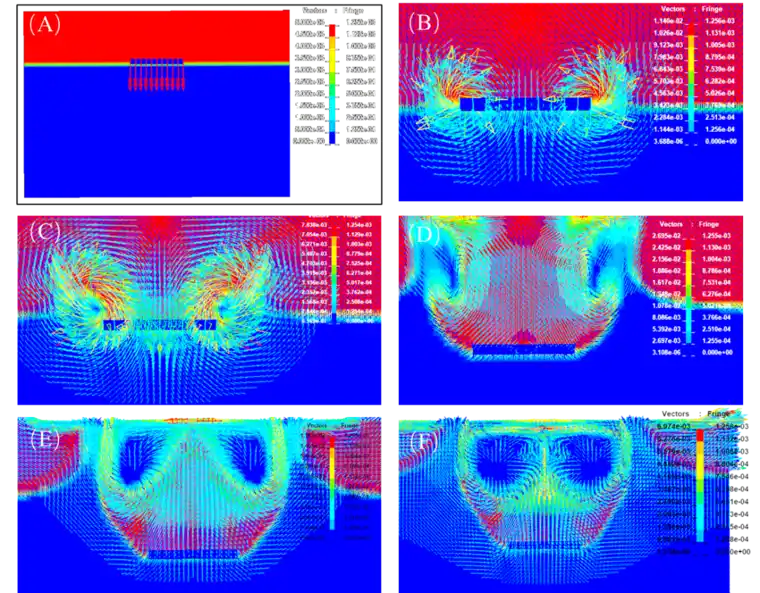
图3金属板速度变化
4.3单元压力时程曲线
在中位处按一定相等距离从上到下依次取7个单元点(如图4所示),记录单元点的压力变化值,在10ms时间内各个单元的压力随时间的变化如图5所示。由曲线可知,从空气进入水介质,单元压力值呈现递增趋势,压力值越来越大,但压力的峰值逐渐滞后。
分析原因:金属板下落中,金属板的动能和重力势能转化成水的动能和势能,因此在初期峰值出现最快,而随着时间的积累,水的总能量是增加的,因此时间越长,峰值越大。
反映在所取中线上的单元压力情况即是:单元6849的压力峰值在2ms就已经出现,但峰值最小,而单元4649的压力峰值在4.8ms才出现,但峰值却较大,为6.8e-6。
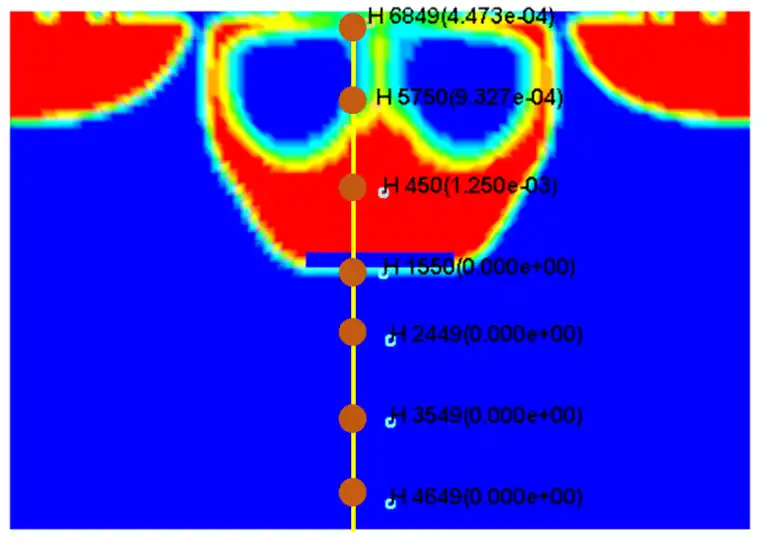
图4中位线单元取点
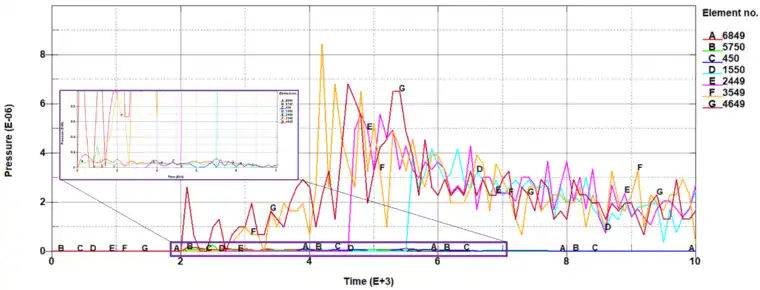
图5单元压力时程变化曲线
5结论
1)本文基于流固耦合算法实现了金属板跌落水中激起的浪花现象模拟,对其他物质的跌落仿真模拟具有借鉴意义。
2)在有限元分析时,本文采用间接法建立有限元算例,这方便了ANSYS和LSDYNA软件之间流固耦合仿真的处理。
3)本文模型采用单层实体网格建模,优点在于:既充分利用了LSDYNA程序中的多物质ALE算法,又大大减小了计算时间(21min)。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删