根据ANSYS的使用者反馈,针对非线性接触问题上的求解,经常会有客户出现不收敛的情况,在调试收敛性上花费大量的时间。本文主要针对ANSYS 接触不收敛问题进行方法上的技巧总结,希望通过本文使大家在ANSYS软件的使用上有更好的体验。
ANSYS接触不收敛的原因有非常多的原因,针对每一种不收敛问题,选择正确的方法都能使不收敛问题解决变得容易起来。在使用软件中,ANSYS接触不收敛原因主要有下面这些原因:
1、接触算法的不正确选择;
2、遗漏了相关的接触对;
3、物体之间接触刚度过大;
4、求解的载荷步较少;
5、奇异;
6、结构发生了刚体位移;
7、结构发生振荡现象;
下面针对这些原因的解决办法进行详细的讲解:
1接触算法的选取原则
ANSYS内部大体上包括5种算法,Pure Penalty,Augmented Lagrange,MPC,Pure Lagrange,Beam。
| 算法 | 应用范围 |
| Pure Penalty | Workbench默认算法,计算速度快 |
| Augmented Lagrange | ANSYS 经典界面默认算法,计算精度较高,收敛性好 |
| Multipoint Constraint (MPC) | 经常和Bonded联合使用,用于大模型的装配定义,可大大降低计算时间,还或用于不同类型单元之间的连接 |
| Lagrange | 常用于模拟接触面之间零穿透并且存在摩擦的情况,例如模拟橡胶——金属之间的接触 |
| Beam | 主要计算梁与梁之间的接触(使用较少) |
在大多数情况下,针对非线性接触问题时候,Augmented Lagrange是最好的收敛算法;当需要研究结构的振荡问题时,由于考虑零渗透问题,选择使用Lagrange方法能更好的提高精度,同时由于零渗透的原因使得计算时间变得更长。
针对非线性接触问题,方法的正确选择,可以使得收敛困难的问题变得容易收敛。
2遗漏接触对
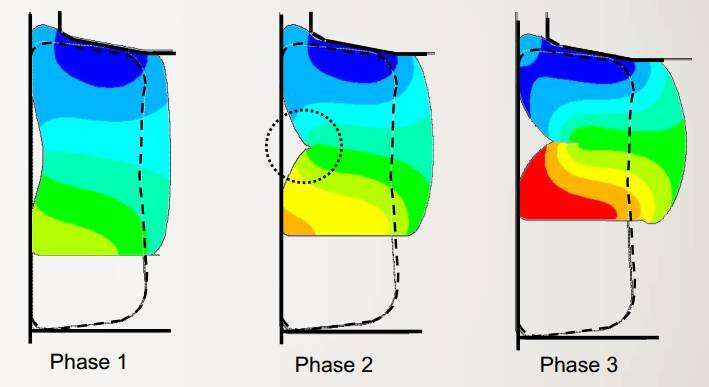
图1、挤压变形示意图
如图1所示,挤压一个塑性材料结构,结构在外力的作用中,中端出现了褶皱,形成了自接触现象。很多时候工程师由于对工程问题的不够了解,使得相关的接触对发生了遗漏。这一部分遗漏的接触对,使得结构发生变形后单元发生了畸变,不仅影响仿真计算结果精度,在很大程度上使得单元发生扭曲造成结构的不收敛现象。
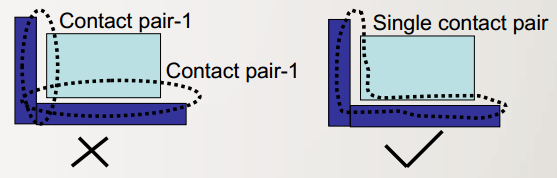
图2、解除对的正确建立
除了保证接触对的正确生成,在另外一个层面上,还需要建立正确的接触对形式,如图2所示,第一种法法将每一个面与对应的面生成接触对,第二种方法将接触对进行整合,作为一个接触对。两种方法虽然在形式上都是正确的,然而使用第一种方法时,结构在两个接触对交接处会数值由于偏差,往往使得接触的收敛变的困难;而第二种方法将接触的面作为一个单一接触能避免这种问题的出现,使得接触的收敛性更好。
3接触刚度大
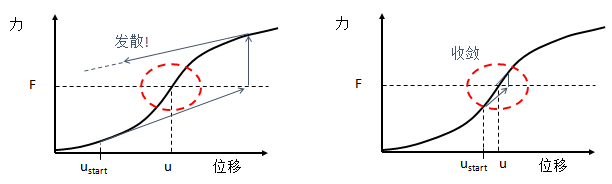
ANSYS求解接触问题的时候,接触刚度对收敛性影响显著。大多数情况下缺省设置有效,但对于以弯曲为主的接触问题,这种缺省设置往往是不能解决问题的。当接触不好收敛的情况下,通过查看收敛曲线,会发现收敛曲线会平行于收敛准则。如下图所示,分别使用FKN=0.1和FKN=0.01两种情况下的接触对收敛曲线,发现选择较小的罚刚度值(FKN),可以是接触收敛更容易。

当调整接触刚度后,虽然可以调节结构的收敛性,然而接触由于刚度的变化使得渗透量变大,因此需要查看结果中结构之间的渗透量,对结果精度进行判断。
4载荷步少
在求解非线性问题的时候,初始时间步必须不断的调试,使得结构的收敛曲线会在收敛半径以内。
如果对于大变形问题,通常需要更多的子步,用以捕捉模型受力过程,复杂的载荷则需要使用重启动来多次条件时间步长。
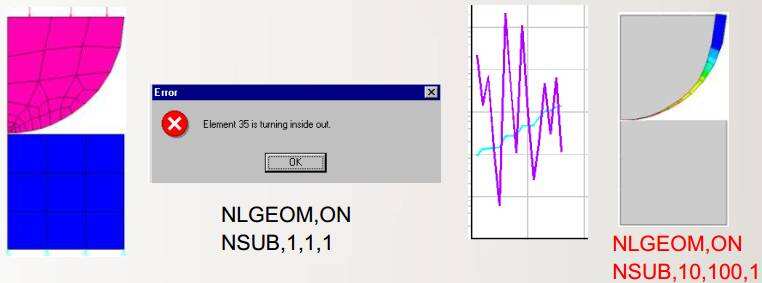
5奇异
结构发生奇异,收敛困难的原因,很多情况都是在物理意义上,有限元模型不准确造成的。例如:如果使用点载荷去做塑性分析,将没有办法获得收敛结果。因为节点上产生了奇异,局部的奇异会使得整个结构不收敛。这个对于接触分析也是一样的。如果使用简化的结果或者使用太粗的网格,造成的接触区域是点接触,那么很有可能使问题不收敛。
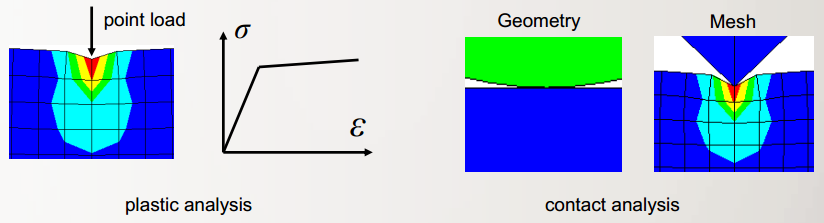
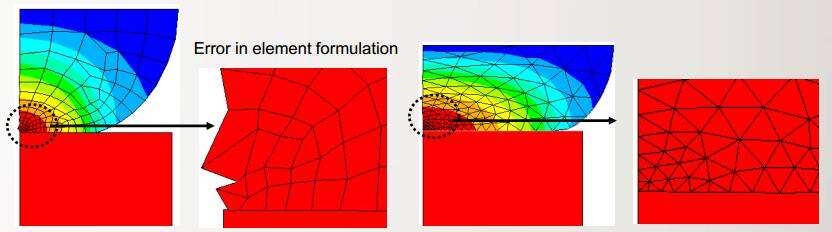
奇异性造成不收敛的另外一个原因是单元中同时夹杂着三角形单元和四边形单元,导致求解单元的方程和单元发生了混乱。如果一些元素在局部扭曲使得结果发生错误,可以尝试使用较粗的网格划分这个区域,以避免这些问题。
6刚体位移
除了网格,单元设置方面导致接触不收敛。由于数值问题导致有限元模型不正确,这个就是我们常说的结构发生了刚体位移。
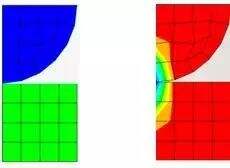
导致刚体位移,大多数情况都是由于建模不严谨导致模型之间有间隙或者穿透,因此需要在软件中关闭间隙或者穿透,或者通过CONTACT Tools对结构的接触渗透间隙值进行审查。
7振荡
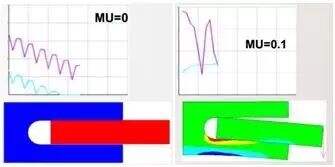
导致结构接触不收敛的另外一个原因是由于结构在受力过程中发生了振荡。当结构发生振动的时,可以通过引入小的摩擦系数加载所有的接触单元上(摩擦系数可以用MU=0.01or0.1)缓解结构振荡的效果,使得接触的收敛性更好。

总结
接触的非线性问题是有限元分析中的重点难点,希望通过本文能解决一部分的接触非线性问题。后续我们将进行更多接触非线性应用技巧的介绍。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删