有限元分析的精度与网格细化：是越细越好吗？

有限元分析时，网格划分越密，计算结果一般来说越趋近于真实解。

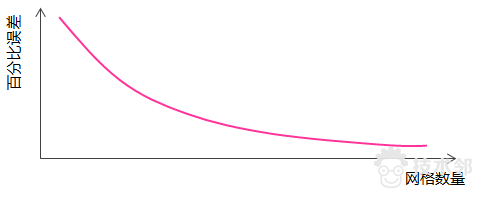
网格划分越密，就直接导致计算的规模和存储空间迅速增加，从而降低计算效率，尤其是对于碰撞、冲击、爆炸、波传播仿真等动力学分析来说。     所以说，在计算效率、存储空间、精确度这三个方面要有所权衡，在满足求解精度的条件下，尽量使得计算效率高、存储空间小。     若将来有一天，计算机技术发展到我们不在为计算效率、存储空间所困扰的话，我想现在的有限元分析工程师可能就失去了他百分之六七十的存在价值了，因为有限元分析已经变得再简单不过了，只要把网格划分的足够密，我们就能快速地得到满意的结果了。

然而，现实是我们没法这么做。对于一个工程问题来说，我们可能在有限元建模，尤其是网格划分上，花费大量的人力、物力，网格划分的好坏在很大程度上依赖于分析人员的实际工作经验，对于网格疏密的把握大致是将所关心的区域划分得细密些、将应力梯度变化大的地方加密些、动力学网格细密度比静力学高、结构分析网格比电磁分析网格稀疏。

正如马远方（来自知乎）所说，除了将网格划分的细密些，提高计算精度的方法还可以通过采用高阶单元实现。目前来说，实现“高阶单元”主要有三种方法，一是提高单元每个节点的自由度数，二是增加每个单元的节点数，三是既增加每个单元节点数又增加每个节点自由度数。

对于单纯增加单元数量提高计算精度的方法，一般称作“h-version mesh refinement”，而通过采用高阶单元提高计算精度的方法称作是“p-version mesh refinement”。当然喽，如果你高兴的话，可以交叉使用这两种手段提高计算精度，暂且称之为“h, p-version mesh refinement”。参看延伸阅读[1]。

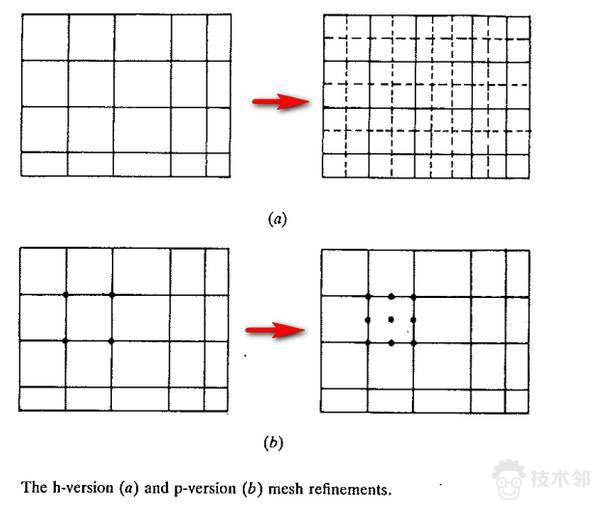
针对增加每个节点自由度的方法实现高阶单元计算的目的，该方法有个较为致命的缺陷，那就是每个自由度物理意义不明显，这也就导致施加载荷和边界条件变得更为困难了，是更困难了，不是不能施加。感兴趣的话，可以尝试读一读文后的延伸阅读[2]，这里打个预防针：数学基础不太好，或者没学过张量分析的同学可以只看看结论就行了。   可以这么说，这是一件很遗憾的事情啦，这也就导致了大多数商业有限元分析软件，如ANSYS、Patran/Nastran、ABAQUS等，使用它们划分网格时，所谓的“高阶单元”通常是指具有更多节点的单元，通过提高节点数量从而提高插值形函数阶数，最终实现提高计算精度的目的。各个软件之间的基本思路几乎都是这样的，还真没见过哪个商业有限元软件是增加每个节点自由度建立高阶单元的，不过在高校里搞搞研究，还是不错的，顺带还可以发个小文章，比如延伸阅读[3]，声明：这篇不是我写的，我也没挂名。

增加节点是可以提高单元阶数，但是节点怎么分布还是有道道的，不是随随便便分布的，推荐感兴趣的童鞋们看看延伸阅读[4]。对于采用均匀节点的情况，插值形函数会出现“龙格现象”，从而降低了插值的精度，不过可以采用非均匀分布的节点消弱这个影响，比如Gauss-Lobatto-Legendre节点、Gauss-Lobatto-Chebyshev节点、Expanded Chebyshev节点。 对于“龙格现象”，可以以一维8节点的三种节点分布形函数为例。对于均匀分布（Equidistant nodes），形函数在单元端部（±1附近）幅值明显超过1，这个就是“龙格现象”，而其它两种节点由于采用的是非均匀分布情况，所以“龙格现象”不明显。要想深入了解，请看延伸阅读[5]。说了这么多，也算是对之前学习研究的一个小结。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删